Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 96

Шаг 1.
Оформляем условие в виде чертежа.

Шаг 2.
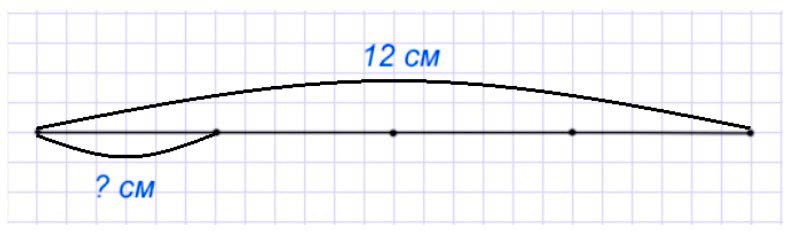
Рассуждаем.

Общая длина полоски – 12 см. Ее разделили на 4 равные части, а взяли одну, то есть, одну четвертую.
Общая длина всей полоски складывается из длины каждого из 4 частей. Значит, чтобы узнать, чему равна длина части, нужно длину полоски разделить на 4.

12 : 4 = 3 (см) − длина закрашенной части.

Шаг 3.
Записываем ответ.

Ответ: 3 см длина одной четвёртой полоски.

Шаг 1.
Оформляем условие в виде чертежа.

Шаг 2.
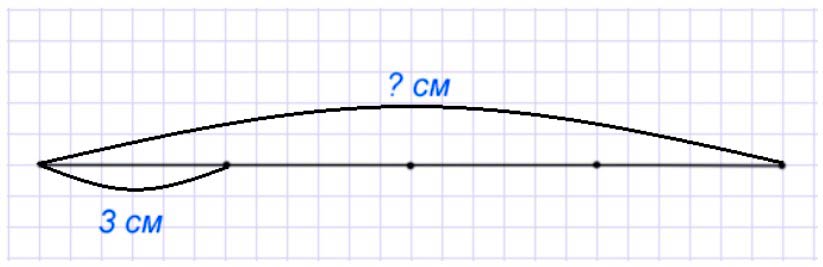
Рассуждаю.

Общая длина всей полоски складывается из длины каждого из 4 частей. Значит, чтобы узнать, чему равна длина целого по части, нужно сложить длину каждой из частей.
Но длина одной части одинаковая, поэтому сложение одинаковых слагаемых можно заменить умножением. И длину одной части нужно умножить на количество этих частей.

3 ∙ 4 = 12 (см) − длина всей полоски.

Шаг 3.
Записываем ответ.

Ответ: 12 см длина всей полоски.

Шаг 1.
Оформляем условие в виде чертежа.

Шаг 2.
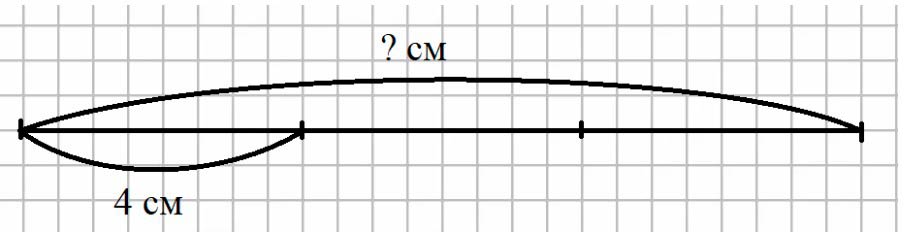
Рассуждаем.

Общая длина полоски неизвестна, но ее разделили на 3 части, а взяли одну, то есть, одну третью.
Общая длина всей полоски складывается из длины каждого из 3 частей. Значит, чтобы узнать, чему равна длина целого по части, нужно сложить длину каждой из частей.
Но длина одной части одинаковая, поэтому сложение одинаковых слагаемых можно заменить умножением. И длину одной части нужно умножить на количество этих частей.

4 ∙ 3 = 12 (см) − длина всего отрезка.

Шаг 3.
Записываем ответ.

Ответ: 12 см длина всего отрезка.

Шаг 1.
Оформляем условие в виде чертежа.

Шаг 2.
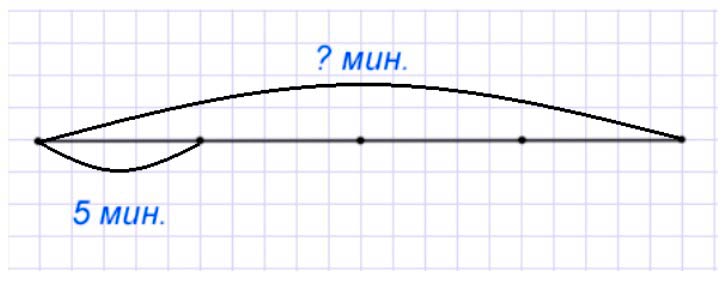
Рассуждаем.

Маленькая перемена длится 5 минут, что составляет четвертую часть большой перемены. То есть, длина большой перемены состоит из четырех маленьких перемен. Значит, что большая перемена длится столько, сколько четыре маленьких перемен.
Тогда, чтобы узнать, сколько длится большая перемена, нужно длину маленькой перемены умножить на 4.

5 ∙ 4 = 20 (мин) – большая перемена.

Шаг 3.
Записываем ответ.

Ответ: 20 минут длится большая перемена.

Шаг 1.
Расставляем порядок действий.

      1       2
(28 + 12) : 4 = 10
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – деление.

     2        1
57 − (37 − 15) = 35
В данном выражении присутствуют действия вычитания и скобки. Вначале выполним вычитание в скобках, а потом вычитание вне скобок.

       2      1
100 − 90 : 10 = 91
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом действие вычитание.

    1    3      2
81 : 9 + 42 : 6 = 16
В данном выражении присутствуют действия сложение и деления. Вначале выполняем действия деления по порядку слева направо, а последним действием – сложение.

   1   3    2
8 · 7 − 6 · 9 = 2
В данном выражении присутствуют действия вычитание и умножения. Вначале выполняем действия умножения по порядку слева направо, а последним действием – вычитание.

    1    3      2
63 : 9 + 72 : 8 = 16
В данном выражении присутствуют действия сложение и деления. Вначале выполняем действия деления по порядку слева направо, а последним действием – сложение.

     2      1
90 − 40 : 10 = 86
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом действие вычитание.

     2      1
14 + 56 : 7 = 22
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом действие сложение.

     1       2
60 − 42 + 8 = 26
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем действия по порядку слева направо.

Шаг 2.
Выполняем вычисления по действиям.

      1       2
(28 + 12) : 4 = 10

1) 28 + 12 = (20 + 10) + (8 + 2) = 30 + 10 = 40

Выполняем сложение по разрядам – десятки складываем с десятками, а единицы – с единицами.

2) 40 : 4 = 10,
где 10 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

     2        1
57 − (37 − 15) = 35

1) 37 – 15 = (30 – 10) + (7 – 5) = 20 + 2 = 22

Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.

2) 57 − 22 = (50 – 20) + (7 – 2) = 30 + 5 = 35

Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.

       2      1
100 − 90 : 10 = 91

1) 90 : 10 = 9, так как 9 · 10 = 90

2) 100 − 9 = (90 + 10) – 9 = 90 + (10 – 9) = 90 + 1 = 91

Представим число 100 в виде суммы чисел 90 и 10. Вначале из числа 10 вычтем число 9, а потом к полученной разности прибавим число 90.

    1    3      2
81 : 9 + 42 : 6 = 16

1) 81 : 9 = 8, так как 9 · 8 = 72
2) 42 : 6 = 7, так как 6 · 7 = 42
3) 9 + 7 = 16

   1   3    2
8 · 7 − 6 · 9 = 2
1) 8 ∙ 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
2) 6 ∙ 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
3) 56 − 54 = (50 – 50) + (6 – 4) = 2
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.

    1    3      2
63 : 9 + 72 : 8 = 16
1) 63 : 9 = 7, так как 9 · 7 = 63
2) 72 : 8 = 9, так как 8 · 9 = 72
3) 7 + 9 = 16

     2      1
90 − 40 : 10 = 86
1) 40 : 10 = 4, так как 4 · 10 = 40
2) 90 − 4 = (80 + 10) – 4 = 80 + (10 – 4) = 80 + 6 = 86

     2      1
14 + 56 : 7 = 22
1) 56 : 7 = 8, так как 7 · 8 = 56
2) 14 + 8 = 14 + (6 + 2) = (14 + 6) + 2 = 20 + 2 = 22

Число 8 представим в виде суммы чисел 6 и 2. Вначале к числу 14 прибавим число 6, а потом прибавим число 2.

     1       2
60 − 42 + 8 = 26
1) 60 – 42 = 18

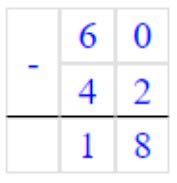
Вычитаем единицы. От числа 0 мы не можем отнять 2.
Занимаем 1 дес. = 10 ед., 10 – 2 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 6 дес., мы занимали 1 дес, осталось 6 – 1 = 5 дес.,
5 – 4 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 18.

2) 18 + 8 = 18 + (2 + 6) = (18 + 2) + 6 = 20 + 6 = 26

Число 8 представим в виде суммы чисел 2 и 6. Вначале к числу 18 прибавим число 2, а потом число 6.

Шаг 3.
Оформляем задание в тетрадь.

(28 + 12) : 4 = 40 : 4 = 10
57 – (37 – 15) = 57 – 22 = 35
100 – 90 : 10 = 100 – 9 = 91

81 : 9 + 42 : 6 = 9 + 7 = 16
8 ∙ 7 – 6 ∙ 9 = 56 – 54 = 2
63 : 9 + 72 : 8 = 7 + 9 = 16

90 – 40 : 10 = 90 – 4 = 86
14 + 56 : 7 = 14 + 8 = 22
60 – 42 + 8 = 18 + 8 = 26

Шаг 1.
Оформляем условие в виде чертежа.

Шаг 2.
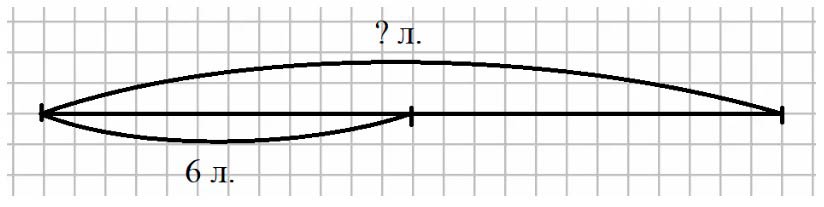
Рассуждаем.

Половина тетради – 6 листов. Значит, что одна вторая всей тетради – это 6 листов. Тогда, чтобы узнать, чему равно количество страниц в тетради, нужно сложить количество листов в каждой части.
Но количество листов в половинах одинаковое, ведь половины равны, значит, сложение одинаковых слагаемых можно заменить умножением.

6 ∙ 2 = 12 (стр.) – в целой тетради.

Шаг 3.
Записываем ответ.

Ответ: в тетради 12 страниц.

Шаг 1.
Начертим фигуру 1.

С помощью циркуля начертим окружность с радиусом 15 мм.
А внутри получившейся окружности начертим квадрат со стороной 20 мм = 2 см.
Разделим квадрат на 4 равных треугольника и раскрасим фигуру по образцу.

Шаг 2.
Начертим фигуру 2.

С помощью линейки начертим квадрат со стороной 20 мм = 2 см.
А внутри квадрата начертим окружность с радиусом 10 мм = 1 см.
Разделим квадрат на 4 равных квадрата со стороной 10 мм = 1 см и раскрасим по образцу.