Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 95

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 3.
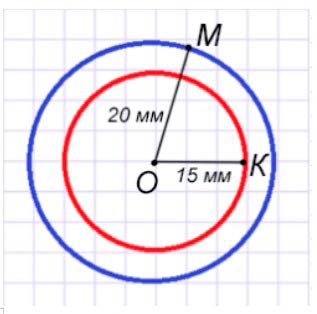
Измерь радиус каждой окружности и начерти окружности с такими же радиусами, но с центром в одной и той же точке.
Ответ:Первая окружность – её радиус = 20 мм Вторая окружность – её радиус = 15 мм

1) Помни о том, что между кругом и окружностью есть разница.
2) Диаметр – отрезок, который проходит через центр и соединяет две любые точки на окружности.
3) Используй специальные приборы: циркуль и линейку.
Измерим радиусы окружностей.
С помощью линейки измерим радиусы в первой и второй окружности.
ОМ = 20 мм = 2 см – радиус первой окружности.
ОК = 15 мм = 1 см 5 мм – радиус второй окружности.
Начертим.
Начертим окружности с радиусами 20 мм и 15 мм с радиусами в одной точке.
Номер 4.
Из 30 кг семян подсолнечника получают 6 кг масла. Сколько килограммов масла можно получить из 25 кг семян подсолнечника?
Ответ:
1-й способ решения:
1) 30 : 6 = 5 (кг) – нужно для получения 1 кг масла.
2) 25 : 5 = 5 (кг) – масла получится
Ответ: 5 кг масла получится всего из 25 кг семян.
2-й способ решения:
25 : (30 : 6) = 25 : 5 = 5 (кг) – из 25 кг семян.
Ответ: 5 кг масла.
Данная задача: вида «расход на 1 кг масла, кол-во семян, общее кол-во масла» характеризуется зависимостями между компонентами:
Расход на 1 кг масла · кол-во семян = общее кол-во масла.
Общее кол-во масла : кол-во семян = расход на 1 кг масла.
Общее кол-во масла : расход на 1 кг масла = кол-во семян.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество семян складывается из количества семян, расходуемых на каждый кг масла. Значит, чтобы узнать, сколько килограмм семечек нужно на приготовление 1 кг масла, нужно общее количество семян разделить на количество полученного масла.
30 : 6 = 5 (кг) − на 1 кг масла.
Продолжаем рассуждение.
Мы узнали, что расход семян на 1 кг масла – 5 кг, а общее количество семян – 25 кг. Значит, нам известен расход семян, общее количество, но неизвестно количество полученного масла.
Поэтому, чтобы узнать, сколько масла получили, нужно общее количество семян разделить на количество семян, расходуемое на 1 кг масла.
25 : 5 = 5 (кг) − из 25 кг семян.
Записываем ответ.
Ответ: 5 кг масла получится.
Решение выражением:
25 : (30 : 6) = 5 (кг), где 30 : 6 – расход семян на 1 кг масла.
Номер 5.
Из 20 кг кедровых орехов можно получить 5 кг масла. Сколько кедровых орехов надо взять, чтобы получить 20 кг масла?
Ответ:
1-й способ решения:
1) 20 : 5 = 4 (кг) – нужно для получения 1 кг масла.
2) 4 · 20 = 80 (кг) – орехов
Ответ: 80 кг орехов надо взять для приготовления 20 кг масла.
2-й способ решения:
20 : 5 · 20 = 4 · 20 = 80 (кг) – на 20 кг масла.
Ответ: 80 кг орехов.
Данная задача: вида «расход орехов на 1 кг масла, количество масла, общее количество орехов» характеризуется зависимостями между компонентами:
Расход орехов на 1 кг масла · кол-во масла = общее кол-во орехов.
Общее кол-во орехов : расход орехов на 1 кг масла = кол-во масла.
Общее кол-во орехов : кол-во масла = расход орехов на 1 кг масла.
Оформляем условие в виде таблицы.

Рассуждаем.
Из 20 кг кедровых орехов можно получить 5 кг масла. Значит, нам известно общее количество орехов и общее количество масла, но неизвестен расход орехов на 1 кг масла.
При этом из таблицы - модели к задаче видно, что общее количество орехов складывается из количества орехов, расходуемых на каждый кг масла. Поэтому, чтобы узнать, сколько орехов расходуется на производство 1 кг орехов, нужно общее количество орехов разделить на количество масла.
20 : 5 = 4 (кг) − на 1 кг масла.
Продолжаем рассуждение.
Мы узнали расход орехов на 1 кг масла, нам известно количество масла, но неизвестно, сколько всего орехов на это было потрачено. Из таблицы видно, что общее количество орехов складывается из количества орехов, потраченных на каждый кг масла. Значит, чтобы узнать, сколько всего орехов было потрачено, нужно сложить количество орехов, затраченных на каждый кг масла.
Но расход орехов на 1 кг масла одинаковый, поэтому сложение одинаковых слагаемых можно заменить умножением.
20 ∙ 4 = 80 (кг) − на 20 кг масла.
Записываем ответ.
Ответ: 80 кг надо взять орехов.
Решение выражением:
20 : 5 · 20 = 80 (кг), где 20 : 5 – расход орехов на 1 кг масла.
Номер 6.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
3 1 2
78 − (72 − 62) · 4 = 38
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия вне скобок – вначале умножение и последним действием вычитание.
3 1 2
37 + (25 − 15) · 3 = 67
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия вне скобок – вначале умножение и последним действием сложение.
3 1 2
49 − (64 − 44) : 2 = 39
В данном выражении присутствуют действия вычитания и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом действия вне скобок – вначале деление и последним действием вычитание.
1 3 2
54 : 9 + 8 · 5 = 46
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие деление, потом умножение и последним действием – сложение.
1 3 2
32 : 8 + 6 · 7 = 46
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие деление, потом умножение и последним действием – сложение.
1 3 2
36 : 4 + 7 · 8 = 65
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие деление, потом умножение и последним действием – сложение.
1 2
80 : 10 · 8 = 64
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
2 1
50 : (10 · 5) = 1
В данном выражении присутствуют действия умножение и деление, а также скобки. Вначале выполняем действие в скобках – умножение, а потом действие вне скобок – деление.
2 1
60 : (2 · 5) = 6
В данном выражении присутствуют действия умножение и деление, а также скобки. Вначале выполняем действие в скобках – умножение, а потом действие вне скобок – деление.
Выполняем вычисления по действиям.
3 1 2
78 − (72 − 62) · 4 = 38
1) 72 – 62 = (70 – 60) + (2 – 2) = 10 + 0 = 10
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.
2) 10 ∙ 4 = 40,
где 10 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
3) 78 – 40 = (70 – 40) + (8 – 0) = 30 + 8 = 38
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.
3 1 2
37 + (25 − 15) · 3 = 67
1) 25 − 15 = (20 – 10) + (5 – 5) = 10 + 0 = 10
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.
2) 10 ∙ 3 = 30,
где 10 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
3) 37 + 30 = (30 + 30) + (7 + 0) = 60 + 7 = 67
Выполняем сложение по разрядам – десятки складываем с десятками, а единицы – с единицами.
3 1 2
49 − (64 − 44) : 2 = 39
1) 64 – 44 = (60 – 40) + (4 – 4) = 20 + 4 = 20
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.
2) 20 : 2 = 10,так как 2 · 10 = 20
3) 49 − 10 = (49 – 10) + (9 – 0) = 30 + 9 = 39
Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.
1 3 2
54 : 9 + 8 · 5 = 46
1) 54 : 9 = 6,так как 9 · 6 = 54
2) 8 ∙ 5 = 40,
где 8 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
3) 6 + 40 = 46
Выполняем сложение по разрядам – десятки складываем с десятками, а единицы – с единицами.
1 3 2
32 : 8 + 6 · 7 = 46
1) 32 : 8 = 4, так как 8 · 4 = 32
2) 6 ∙ 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
3) 4 + 42 = 40 + (4 + 2) = 40 + 6 = 46
Выполняем сложение по разрядам – десятки складываем с десятками, а единицы – с единицами.
1 3 2
36 : 4 + 7 · 8 = 65
1) 36 : 4 = 9,так как 4 · 9 = 36
2) 7 ∙ 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
3) 9 + 56 = (4 + 5) + 56 = (56 + 4) + 5 = 60 + 5 = 65
Представим число 9 в виде суммы чисел 4 и 5. В начале к числу 56 прибавим число 4, а потом число 5.
1 2
80 : 10 · 8 = 64
1) 80 : 10 = 8,так как 8 · 10 = 80
2) 8 ∙ 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2 1
50 : (10 · 5) = 1
1) 10 ∙ 5 = 50,
где 10 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
2) 50 : 50 = 1,
Если число разделить на само себя, то получим 1.
2 1
60 : (2 · 5) = 6
1) 2 ∙ 5 = 10,
где 2 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
2) 60 : 10 = 6, так как 6 · 10 = 60
Оформляем задание в тетрадь.
78 – (72 – 62) · 4 = 78 – 10 · 4 = 78 – 40 = 38
37 + (25 – 15) · 3 = 37 + 10 · 3 = 37 + 30 = 67
49 – (64 – 44) : 2 = 49 – 20 : 2 = 49 – 10 = 39
54 : 8 + 8 · 5 = 6 + 40 = 46
32 : 8 + 6 · 7 = 4 + 42 = 46
36 : 4 + 7 · 8 = 9 + 56 = 65
80 : 10 · 8 = 8 · 8 = 64
50 : (10 · 5) = 50 : 50 = 1
60 : (2 · 5) = 60 : 10 = 6
Номер 7.
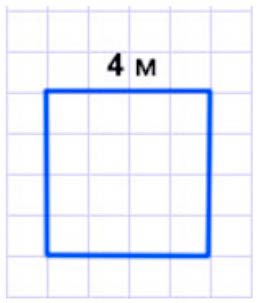
Папа и Лёня делают цветник квадратной формы. Папа сказал: «Сделаем так, чтобы сторона нашего квадрата была на 12 м меньше его периметра». Узнай, какой будет длина стороны этого цветника, и начерти его план, на котором 1 см будет изображать 2 м.
Ответ:
Чтобы узнать, чему равен периметр квадрата, нужно измерить сторону квадрата, а полученное значение умножить на 4, потому что у квадрата все стороны равны.
Рассуждаем.
Периметр квадрата – сумма длин всех его сторон.
Мы знаем, что разница между периметром и стороной квадрата равна 12 см.
Если из периметра квадрата вычесть длину одной стороны, то получим сумму трёх сторон квадрата.
Длины сторон квадрата равны, значит сумма трёх сторон квадрата равна 12 см.
Чтобы узнать, чему равняется длина одной стороны квадрата нужно сумму трёх сторон квадрата разделить на количество сторон.
12 : 3 = 4 (см) – длина одной стороны квадрата.
Делаем проверку.
Пускай, сторона квадрата равна 4 м.
Тогда периметр квадрата равен 4 м · 4 = 16 м.
Сторона квадрата на 12 м меньше периметра, значит, проверяю:
16 м – 4 м = 12 м.
Условие задания выполняется, значит, сторона участка – 4 метра.
Начертим.
Масштаб чертежа участка на плане 1 см : 2 метрам.
Значит, 1 см на плане будет изображать 2 м на местности, то 4 м – будет изображать 2 см или 4 клетки.
Тогда, чертим квадрат со сторон 2 см.
Задание внизу страницы
Начерти в тетради любую окружность. Проведи в ней радиус и измерь его.
Ответ:
1) Помни о том, что окружность – это граница круга, расположенная на плоскости.
2) Радиус – отрезок, который соединяет центр окружности с любой точкой на окружности.
3) Используй специальные приборы: циркуль и линейку.
Начертим окружность.
Окружность чертим с помощью циркуля.
Для этого острый конец циркуля должен оставаться в одной точке и расстояние между ножками циркуля не должно меняться.
Окружность состоит из точек, которые равноудалены от одной заданной точки. Это точка называется центром окружности – точка О.
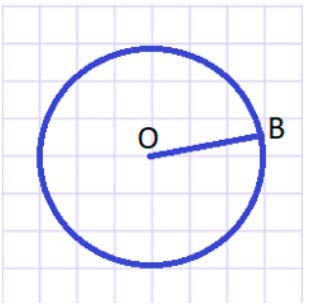
Измерим радиус окружности.
ОВ – радиус окружности.
С помощью линейки измерим отрезок ОВ.
ОВ = 15 мм = 1 см 5 мм.
Задание на полях страницы
Какое число лишнее?

Вариант 1: лишнее число 9, так как оно нечетное. Вариант 2: лишнее число 10, так как оно двузначное.
Чтобы понять какое число лишнее, проанализируй их все: какие они, из какого количества знаков состоят, на какие числа делятся.
Рассуждаем.
Опишем каждое число с точки зрения разных признаков:
4 – однозначное, четное, делится без остатка на 2, 4.
8 – однозначное, четное, делится без остатка на 2, 4, 8.
6 – однозначное, четное, делится без остатка на 2, 3.
9 – однозначное, нечетное, делится без остатка на 3, 9.
2 – однозначное, четное, делится без остатка на 2.
10 – двузначное, четное, делится без остатка на 2, 5, 10.
Делаем вывод.
Таким образом, лишними могут быть:
1) число 10, потому что оно единственное двузначное.
2) число 9, потому что оно нечетное, а все другие – четные.
Записываем ответ.
Ответ: лишнее число 9, так как оно не четное, не делится на 2;
Лишнее число 10, так как оно двузначное, а остальные однозначные.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.