Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 87

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 7.
Реши уравнения.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действиями вычитания, сложения и умножения.
Рассуждение.
75 + х = 90,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
80 – к = 42,
к – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
6 · n = 54,
n – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Решаем уравнения.
75 + x = 90
x = 90 − 75
x = 15
80 − k = 42
k = 80 − 42
k = 38
6 ∙ n = 54
n = 54 : 6
n = 9
Делаем проверку.
75 + х = 90
Проверка: вместо х подставим число 15.
75 + 15 = (70 + 10) + (5 + 5) = 80 + 10 = 90
90 = 90 – верно.
80 – k = 42
Проверка: вместо k подставим число 38.
80 – 38 = (70 + 10) – (30 + 8) = (70 – 30) + (10 – 8) = 40 + 2 = 42
42 = 42 – верно.
6 · n = 54
Проверка: вместо n подставим число 9.
6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
54 = 54 – верно.
Номер 8.
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD.
2) Найди двумя способами площадь прямоугольника ABCD.

1) Площадь BCKE:
BC ∙ BE = 2 ∙ 2 = 4 (см2)
Площадь AEKD:
АЕ ∙ DA = 3 ∙ 2 = 6 (см2)
2) Площадь BCDA:
1-й способ решения:
Измеряем стороны прямоугольника BCDA:
BC = 2 см
CD = 5 см
Площадь BCDA:
BC ∙ CD = 2 ∙ 5 = 10(см2)
2-й способ решения:
Складываю площади прямоугольников BCKE и AEKD, значит, площадь DCDA:
4 + 6 = 10 (см2)
Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
С помощью линейки измерим стороны.
В прямоугольнике ВСКЕ все стороны равны:
ВС = ЕК = СК = ВЕ = 2 см
В прямоугольнике ЕКDA стороны попарно равны:
КD = EA = 3 см
КЕ = AD = 2 см
Вычислим площади фигур.
ВСКЕ – квадрат, так как у него все сторны равны. Чтобы вычислить площадь квадрата нужно длину умножить на ширину.
2 · 2 = 4 (см2) – площадь ВСКЕ
ЕКDA – прямоугольник. Чтобы вычислить площадь прямоугольника нужно длину умножить на ширину.
2 · 3 = 6 (см2) – площадь ЕКDA
Записываем ответ.
Ответ: 4 см2 и 6 см2.
Узнаем длину ширины и длины.
СВ = DA = 2 см
CD = BE = 2 см + 3 см = 5 см
Вычислим площадь ABCD.
Вычислить площадь АВСD можно двумя способами:
1) Площадь АВСD равна сумме площадей фигур ВСКЕ и ЕКDA. Значит, чтобы узнать, чему арвна площадь нужно площади двух фигур сложить:
4 + 6 = 10 (см2) – площадь АВСD
2) Чтобы вычислить площадь прямоугольника нужно длину умножить на ширину.
2 · 5 = 10 (см2) – площадь АВСD
Записываем ответ.
Ответ: 10 см2.
Номер 9.
1) Сделай такой же чертеж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2).
2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD – и на сколько квадратных сантиметров.

1) Площадь OKD = 3 см2
Площадь OKEA = 9 см2
Площадь NPLS = 9 см2
Площадь NPT = 3 см2
2) Площадь BCKE = 4 см2
Площадь OKD = 3 см2
4 см2 > 3 см2 на 1 см2
ПОДРОБНО:
Задание 1.
Фигуры с общей стороной OK: треугольник OKD и четырёхугольник OKEA.
Площадь OKD = (OD ∙ KD) : 2
2 ∙ 3 : 2 = 6 : 2 = 3см2
Площадь OKEA = EKDA − OKD
4 ∙ 3 − 3 = 12 − 3 = 9 см2
Фигуры с общей стороной NP:
треугольник NPS, квадрат NPLS, треугольник NPT и прямоугольник NPTM.
Площадь квадрата NPLS = NP ∙ LS
3 ∙ 3 = 9 см2
Площадь NPS = NPLS : 2
Площадь NPTM = NP ∙ NM
3 ∙ 2 = 6 см2
Площадь NPT = NPTM : 2
6 : 2 = 3 см2
Задание 2.
Площадь BCKE = BC ∙ CK
4 ∙ 1 = 4 см2
Площадь OKD = (OD ∙ KD) : 2
2 ∙ 3 : 2 = 6 : 2 = 3 см2
Площадь OKD меньше площади BCKE.
4 − 3 = 1 см2
Ответ: Площадь OKD меньше площади BCKE на 1 см2.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Но у фигур сложных, т.е. у которых площадь нельзя вычислить по формуле, нужно поступать иначе. У сложных фигур площадь фигуры равна сумме площадей фигур, из которых она состоит.
Начертим рисунок 1.
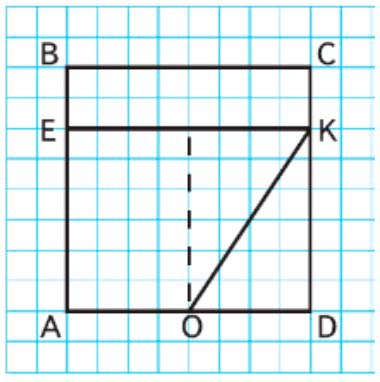
Общая сторона OK есть у трёх фигур:
треугольника OKD,
четырехугольника OKEA,
пятиугольника OKCBA.
Измерим нужные стороны этих фигур (2 клетки = 1 см)
ОD = 2 см
КD = 3 см
ЕК = 4 см
ВС = 4 см
СD = 4 см
Вычислим площади фигур.
Треугольника ОКD в 2 раза меньше прямоугольника со сторонами 3 см и 2 см, значит и площадь треугольника в 2 раза меньше площади прямоугольника.
Найдём площадь прямоугольника со сторонами 3 см и 2 см.
3 см · 2 см = 6 (см2) – площадь прямоугольника.
Теперь найдём площадь треугольника, разделим площадь прямоугольника на 2:
6 : 2 = 3 см2 – площадь треугольника OKD.
Площадь четырехугольника ОКЕА меньше площади прямоугольника ЕКDА на площадь треугольника ОКD. Значит, чтобы найти площадь четырёхугольника ОКЕА нужно из площади прямоугольника ЕКDA вычесть площадь треугольника ОКD.
Найдём площадь ЕКDA:
ЕК ∙ КD = 4 см ∙ 3 см = 12 см2 – площадь ЕКDА.
Найдём площадь ОКЕА, зная что площадь треугольника ОКD равна 3 см2
12 см2 — 3 см2 = 9 см2 – площадь ОКЕА.
Площадь ОКСВА состоит из площади фигур прямоугольника ЕВСК и четырёхугольника ОКЕА. Значит, чтобы узнать площадь фигуры ОКСВА нужно сложить площади фигур ЕВСК и ОКЕА.
Найдём площадь ЕВСК:
ЕВ = 1 см и ВС = 4 см.
1 · 4 = 4 (см2) – площадь ЕВСК.
Найдём площадь ОКСВА, зная что площадь ОКЕА равна 9
4 + 9 = 13 (см2) – полощадь ОКСВА.
Записываем ответ.
Ответ: 3 см2 – площадь треугольника OKD; 9 см2 – площадь ОКЕА; 13 (см2) – полощадь ОКСВА.
Начертим фигуру 2.
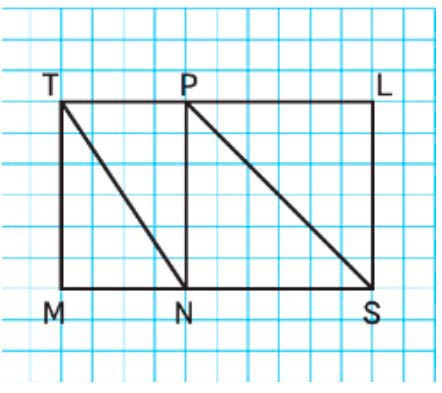
Вычислим площади фигур.
Общая сторона NP есть у четырёх фигур:
треугольника NPS,
квадрата NPLS,
треугольника NPT,
прямоугольника NPTM.
Измерим нужные стороны этих фигур (2 клетки = 1 см)
NP = 3 см
NS = 3 см
РТ = 2 см
ТМ = 3 см
Площадь NPLS можно вычислить, умножив длину на ширину:
NP ∙ NS = 3 см ∙ 3 см = 9 см2 – площадь NPLS.
Площадь треугольника NPS в 2 раза меньше прямоугольника со сторонами 3 см и 3 см, то есть площади NPLS.
3 см · 3 см = 9 см2 = 900 мм2 – площадь прямоугольника со сторонами 3 см.
так как 1 см2 = 10 мм ∙ 10 мм = 100 мм2.
9 см2 : 2 = 900 мм2 : 2 = 450 мм2 – площадь треугольника NPS.
Площадь NPTM можно вычислить, умножив длину на ширину:
ТМ ∙ РТ = 3 см ∙ 2 см = 6 см2 – площадь NPTM.
Площадь треугольника NPT в 2 раза меньше площади NPTM.
6 см2 : 2 = 3 см2 – площадь NPT.
Записываем ответ.
Ответ: 9 см2 – площадь NPLS, 450 мм2 – площадь треугольника NPS, 6 см2 – площадь NPTM, 3 см2 – площадь NPT.
Вычислим площади фигур.
Чтобы сказать, площадь какой фигуры меньше, нужно вначале вычислить площади фигур.
ВСКЕ – прямоугольник. Чтобы найти его площадь нужно длину умножить на ширину.
ВЕ = 1 см
ВС = 4 см
1 · 4 = 4 (см2) – площадь ВСКЕ
ОКD – треугольник, он в два раза меньше прямоугольника со сторонами 3 см и 2 см. Значит и площадь будет в два раза меньше.
Найдём площадь прямоугольника со сторонами 3 см и 2 см.
3 см · 2 см = 6 (см2) – площадь прямоугольника.
Теперь найдём площадь треугольника, разделив площадь прямоугольника на 2:
6 : 2 = 3 (см2) – площадь треугольника OKD.
Сравним площади фигур.
Площадь ВСКЕ = 4 см2
Площадь треугольника OKD = 3 см2
4 см2 > 3 см2
Значит площадь треугольника ОКD меньше площади прямоугольника ВСКЕ.
Чтобы узнать на сколько одна площадь меньше другой, нужно из большей площади вычесть меньшую площадь:
4 – 3 = 1 (см2) – на сколько площадь треугольника ОКD меньше площади прмяугольника ВСКЕ.
Записываем ответ.
Ответ: площадь треугольника ОКD ментше площади прямуогогльника ВСКЕ на 1 см2.
Задание внизу страницы
На сколько 9 меньше, чем 72?
Во сколько раз 6 меньше, чем 54?
9 меньше чем 72 на 63, потому что 72 - 9 = 63 6 меньше чем 54 в 9 раз, потому что 54 : 6 = 9.
1) Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
2) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
Рассуждаем.
72 – 9 = 72 – (2 + 7) = (72 – 2) – 7 = 70 – 7 = 63
Число 9 представим в виде суммы числе 2 и 7. Из числа 72 вначале вычтем число 2, а потом вычтем число 7.
54 : 6 = 9, так как 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
1) 72 − 9 = 63 – на сколько число 9 меньше, чем 72.
2) 54 : 6 = 9 (раз) – во сколько раз число 6 меньше, чем 54.
Задание на полях страницы
Цепочка:

54 : 9 = 6 6 ∙ 7 = 42 42 + 58 = 100 100 − 75 = 25
1) Выполни действия по порядку.
2) Первая зеленая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
54 : 9 = 6, так как 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
42 + 58 = (40 + 50) + (2 + 8) = 90 + 10 = 100
Складываем по разрядам: единицы складываем с единицами, а десятки - с десятками.
100 – 75 = 25
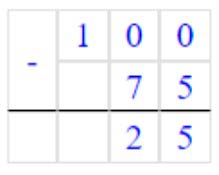
Оформляем задание в тетрадь.
54 : 9 = 6
6 ∙ 7 = 42
42 + 58 = 100
100 – 75 = 25
54 : 9 = 6 → 6 · 7 = 42 → 42 + 58 = 100 → 100 – 75 = 25
Номер 4.
Начерти в тетради такие фигуры. Проведи в каждой фигуре один отрезок так, чтобы стало видно, что все три фигуры имеют одинаковые площади.
В каких фигурах проведённый отрезок будет осью симметрии фигуры?


Ответ: квадрат, треугольник
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину. Вычисляется умножением.
2) Но у сложных фигур, таких, как 2, 3, вычислить площадь по формуле невозможно. Тогда выразить его площадь нужно в квадратных единицах, т.е. клеточках.
Рассуждаем.
Вторая и третья фигуры – сложные, т.е. вычислить их площадь по формуле невозможно.
Чтобы доказать, что у всех фигур площади равные, сначала вычислю площадь первой фигуры.
Сделаю это практически, т.е. пересчетом.
Зеленый квадрат составлен из 16 клеток, значит площадь квадрата равна 16 клеток.
Продолжаем рассуждение.
Вторая фигура – желтый треугольник. Если разбить данную фигуру пополам, то будет видно, что две части этой фигуры – это две части квадрата номер 1, но части расположены иначе.
-(2023).jpg)
Если одну часть треугольника поставить на другую часть, то получится квадрат со стороной 4 клетки, значит площадь треугольника равна 16 клеток.
Продолжаем рассуждение.
Фигура номер 3 также представляет собой две части квадрата номер 1, но расположенные иначе. При этом все равно площади всех трех фигур одинаковые – 16 клеток, только равные части, из которых они составлены, расположены иначе.
-(2023).jpg)
Если одну часть треугольника поставить на другую часть, то получится квадрат со стороной 4 клетки, значит площадь треугольника равна 16 клеток.
Начертим ось симметрии.
-(2023).jpg)
В квадрате и треугольнике – отрезок будет осью симметрии.
В фигуре 3 – оси симметрии нет, так как при наложении части не совпадут.
Номер 5.
Поставь в кружки знаки арифметических действий так, чтобы равенства стали верными. Если надо, используй скобки.
8 ◯ 4 ◯ 2 = 34 8 ◯ 4 ◯ 2 = 10 8 ◯ 4 ◯ 2 = 4 8 ◯ 4 ◯ 2 = 14 8 ◯ 4 ◯ 2 = 1 8 ◯ 4 ◯ 2 = 30 8 ◯ 4 ◯ 2 = 48 8 ◯ 4 ◯ 2 = 64
Ответ:8 · 4 + 2 = 34 8 + 4 – 2 = 10 8 : 4 + 2 = 4 8 + 4 + 2 = 14 8 : 4 : 2 = 1 8 · 4 – 2 = 30 8 · (4 + 2) = 48 8 · (4 · 2) = 64
1) Меняй знаки арифметических действий, складывай, умножай, вычитай и дели, пока не найдешь верное решение.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставим знаки действия, чтобы выражения стали верными.
8 · 4 + 2 = 34
В данном выражении присутствуют знаки действия сложение и умножение. Вначале выполним действие умножение, а потом – сложение.
8 + 4 – 2 = 10
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполним действия по порядку слева направо.
8 : 4 + 2 = 4
В данном выражении присутствуют знаки действия сложение и деление. Вначале выполним действие деление, а потом – сложение.
8 + 4 + 2 = 14
В данном выражении присутствуют действия сложения– они равносильны. Выполним действия по порядку слева направо.
8 : 4 : 2 = 1
В данном выражении присутствуют действия деления – они равносильны. Выполним действия по порядку слева направо.
8 · 4 – 2 = 30
В данном выражении присутствуют знаки действия вычитание и умножение. Вначале выполним действие умножение, а потом – вычитание.
8 · (4 + 2) = 48
В данном выражении присутствуют знаки действия сложение и умножение, а также скобки. Вначале выполним действие в скобках - сложение, а потом действие вне скобок - умножение.
8 · (4 · 2) = 64
В данном выражении присутствуют знаки действия умножения, а также скобки. Вначале выполним действие в скобках - умножение, а потом действие вне скобок - умножение.
Проверим вычисления.
1 2
8 · 4 + 2 = 34
1) 8 ∙ 4 = 32
2) 32 + 2 = 34
1 2
8 + 4 − 2 = 10
1) 8 + 4 = 12
2) 12 – 2 = 10
1 2
8 : 4 + 2 = 4
1) 8 : 4 = 2
2) 2 + 2 = 4
1 2
8 + 4 + 2 = 14
1) 8 + 4 = 12
2) 12 + 2 = 14
1 2
8 : 4 : 2 = 1
1) 8 : 4 = 2
2) 2 : 2 = 1
1 2
8 ∙ 4 – 2 = 30
1) 8 ∙ 4 = 32
2) 32 – 2 = 30
2 1
8 ∙ (4 + 2) = 48
1) 4 + 2 = 6
2) 8 ∙ 6 = 48
2 1
8 ∙ (4 ∙ 2) = 64
1) 4 ∙ 2 = 8
2) 8 ∙ 8 = 64
Оформляем задание в тетрадь.
8 ∙ 4 + 2 = 32 + 2 = 34
8 + 4 − 2 = 12 – 2 = 10
8 : 4 + 2 = 2 + 2 = 4
8 + 4 + 2 = 12 + 2 = 14
8 : 4 : 2 = 2 : 2 = 1
8 ∙ 4 − 2 = 32 – 2 = 30
8 ∙ (4 + 2) = 8 · 6 = 48
8 ∙ (4 ∙ 2) = 8 · 8 = 64
Номер 6.
Вычислительная машина работает как показано на картинке:
1) Какое число будет получаться на выходе из машины, если в неё ввести число: 3, 8, 2, 11, 14? 2) Какое число ввели в машину, если на выходе из машины получили число 3?

1) (3 + 5) · 2 = 16
(8 – 5) · 3 = 9
(2 + 5) · 2 = 14
(11 – 5) · 3 = 18
(14 – 5 ) · 3 = 27
2) 3 : 3 = 1 + 5 = 6
6 > 5 — да
(6 – 5) · 3 = 3
Вычислительная машина, это машина, в которой с введенным числом происходят некоторые действия. Она может умножать, делить, увеличивать на некоторое количество единиц или уменьшать.
Опишем процесс работы вычислительной машины.
1) Число поступает в машину, машина проверяет, больше это число 5 или меньше.
2) Если число меньше 5, то машина увеличивает число на 5 единиц, а затем – увеличивает суммы вдвое.
Если число больше 5, то машина уменьшает введенное число на 5 единиц, а полученную разность увеличивают в 3 раза.
3) На выходе получаем число.
Вычисляем по этапам.
Проделаем все операции с введенными числами: 3, 8, 2, 11, 14, чтобы пронаблюдать работу вычислительной машины:
Число 3.
1) 3 < 5
2) Увеличиваем число на 5, а затем увеличиваем сумму в 2 раза.
(3 + 5) · 2 = 8 · 2 = 16
3) На выходе получаем число 16.
Число 8.
1) 8 > 5,
2) Уменьшаем число на 5, а затем полученную разность увеличиваем в 3 раза.
(8 – 5) · 3 = 3 · 3 = 9
3) На выходе получаем число 9.
Число 2.
1) 2 < 5,
2) Увеличиваем число на 5, а затем увеличиваем сумму в 2 раза.
(2 + 5) · 2 = 7 · 2 = 14
3) На выходе получаем число 14.
Число 11.
1) 11 > 5,
2) Уменьшаем число на 5, а затем полученную разность увеличиваем в 3 раза.
(11 – 5) · 3 = 6 · 3 = 18
3) На выходе получаем число 18.
Число 14.
1) 14 > 5
2) Уменьшаем число на 5, а затем полученную разность увеличиваем в 3 раза.
(14 – 5) · 3 = 9 · 3 = 27
3) На выходе получаем число 27.
Как найти введённое число.
Чтобы понять, какое число ввели в машину, если на выходе из машины получили число 3, нужно выполнить все действия обратные данным, т.е. умножение – деление, вычитание – сложение, сложение – вычитание, деление – умножение.
Вместо окошка подставлю х.
Тогда получаю уравнение: (х – 5) · 3 = 3.
Решаю его, чтобы понять, какое число ввели в вычислительную машину.
(х – 5) · 3 = 3
х – 5 = 3 : 3
х – 5 = 1
х = 1 + 5
х = 6
Значит, в вычислительную машину было введено число 6.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.