Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 85

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Деление нуля на число
Номер 1.
Реши с устным объяснением.
Ответ:4 ∙ 6 = 24 1 ∙ 8 = 8 0 ∙ 4 = 0 6 ∙ 4 = 24 8 ∙ 1 = 8 4 ∙ 0 = 0 24 : 6 = 4 8 : 8 = 1 0 : 4 = 0 24 : 4 = 6 8 : 1 = 8 0 : 8 = 0
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Выполним умножение.
4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Выполним деление.
24 : 6 = 4, так как 6 · 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
24 : 4 = 6, так как 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Выполним умножение и деление на 1.
1 · 8 = 8,
так как если 1 умножить на любое число, то получится это же число.
8 · 1 = 8,
так как если любое число умножить на единицу, то получится число, которое умножали.
8 : 8 = 1,
так как если любое число разделить на само себя, то получится единица.
8 : 1 = 8,
так как если любое число разделить на 1, то получится число, которое делили.
Выполним умножение и деление на 0.
0 · 4 = 0,
так как если 0 умножить на любое число, то получится число, на которое умножали.
4 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
0 : 4 = 0,
так как если 0 разделить на любое число, то получится 0.
0 : 8 = 0,
так как если 0 разделить на любое число, то получится 0.
Оформляем задание в тетрадь.
4 ∙ 6 = 24 8 : 8 = 1
6 ∙ 4 = 24 8 : 1 = 8
24 : 6 = 4 0 ∙ 4 = 0
24 : 4 = 6 4 ∙ 0 = 0
1 ∙ 8 = 8 0 : 4 = 0
8 ∙ 1 = 8 0 : 8 = 0
Номер 2.
Закончи вывод и приведи свои примеры.
При делении нуля на любое другое число, не равное 0, получается ... .
При делении нуля на любое другое число, не равное 0, получается нуль. 0 : 17 = 0, 0 : 5 = 0, 0 : 7 = 0.
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Продолжим фразу.
При делении нуля на любое другое число, не равное 0, получается 0.
Приведём примеры.
0 : 17 = 0,
0 : 5 = 0,
0 : 7 = 0.
Если произведение 0 разделить на b (при этом b неравно 0), то получим 0.
Номер 3.
1) Запиши названия всех треугольников, имеющих: общую вершину – точку А; общую сторону – отрезок АМ.
2) Запиши названия всех четырехугольников.

1) Общая вершина A – ABK. ABC. ABN, CAN, AND, AMD, ABD, AKM. Общая сторона – отрезок АМ: AMB, AMD, AMK. 2) KCNМ, DKСN, ACND, ABND.
1) Треугольник – геометрическая фигура, у которой 3 угла, 3 вершины и 3 стороны.
2) Четырехугольник – геометрическая фигура, у которой 4 угла и 4 стороны.
Рассуждаем.
Треугольники, имеющие общую вершину − точку A:
ΔABC, ΔABD, ΔABK, ΔABM, ΔABN, ΔACN, ΔADK, ΔADM, ΔADN, ΔAKM.
Проилюстрируем.
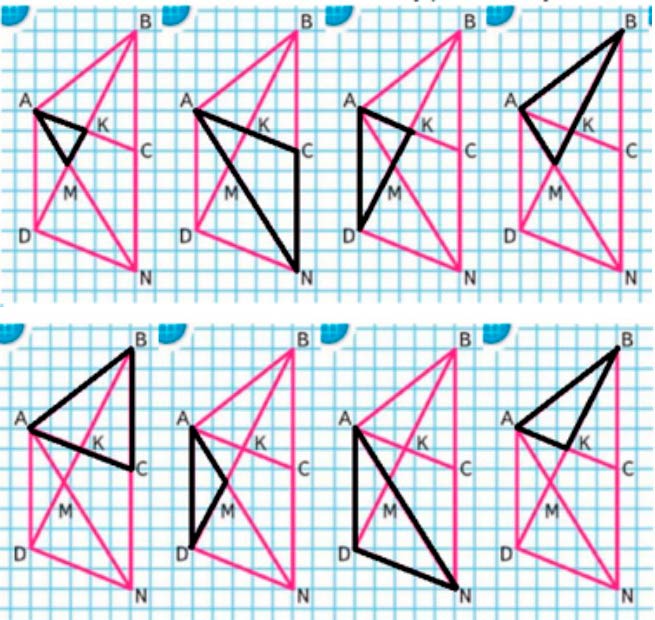
Продолжаем рассуждение.
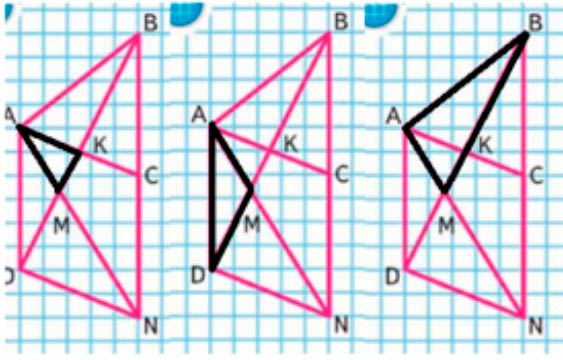
Треугольники, имеющие общую сторону − отрезок AM:
ΔAMB, ΔAMD, ΔAMK.
Проилюстрируем.
Рассуждаем.
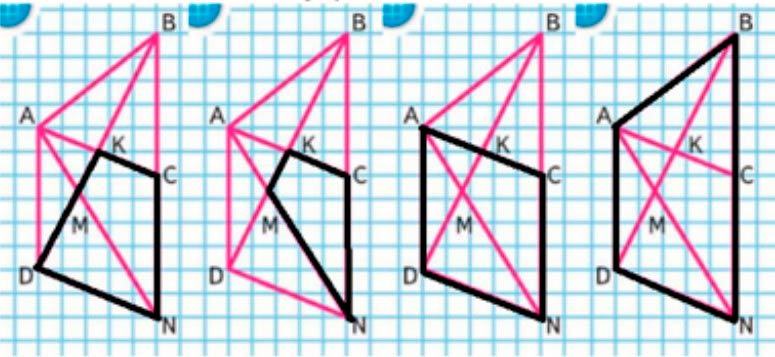
Четырехугольники: ABND, ACND, MKCN, DKCN.
Проилюстрируем.
Номер 4.
У Юры 3 монеты по ☐ р. и еще ☐ р. Сколько всего денег у Юры?
Дополни условие и реши задачу.
У Юры 3 монеты по 5 рублей, и ещё 10 рублей. Сколько всего денег у Юры?
1-й способ решения: 5 ∙ 3 + 10 = 25 (руб.) – у Юры всего Ответ: 25 рублей всего у Юры.
2-й способ решения: 1) 3 ∙ 5 = 15 (руб.) – сумма трёх монет по 5 рублей. 2) 15 + 10 = 25 (руб.) – вся сумма. Ответ: 25 рублей.
Данная задача: вида «номинал одной монеты, количество монет, общее количество денег» характеризуется зависимостями между компонентами:
Номинал 1 монеты · кол-во монет = общее кол-во денег.
Общее кол-во денег : номинал 1 монеты = кол-во монет.
Общее кол-во денег : кол-во монет = номинал 1 монеты.
Оформляем условие в виде кратуой записи.
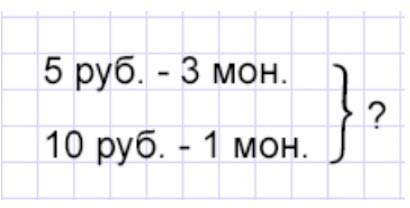
Рассуждаем.
Общее количество монет Юры складывается из количества денег в каждой монете. Значит, чтобы узнать, сколько всего денег было у Юры, нужно сложить количество денег каждой монеты.
Но номинал одной монеты одинаковый, значит, сложение одинаковых слагаемых можно заменить умножением.
5 · 3 = 15 (руб.) – количество денег по 5 рублей.
Продолжаем рассуждение.
Общее количество денег складывается из количества денег первой группы и второй группы. Значит, чтобы узнать, сколько всего денег было в Юры, нужно сложить количество денег каждой группы.
15 + 10 = 25 (руб.) – всего денег у Юры.
Записываем ответ.
Ответ: 25 рублей всего у Юры.
Решение выражением:
5 · 3 + 10 = 25 (руб.), где 5 · 3 – количество денег пятирублёвыми монетами.
Номер 5.
На рынок привезли 48 кг слив в ящиках, по 8 кг в каждом, и столько же ящиков груш, по 9 кг. Сколько килограммов груш привезли?
Ответ:
1-й способ решения: 1) 48 : 8 = 6 (ящ.) – слив привезли. 2) 9 ∙ 6 = 54 (кг) груш привезли Ответ: 54 кг груш привезли.
2-й способ решения: 48 : 8 ∙ 9 = 6 ∙ 9 = 54 (кг) – груш. Ответ: 54 кг.
Данная задача: вида «масса 1 ящика, кол-во ящиков, общее кол-во груш» характеризуется зависимостями между компонентами:
Масса 1 ящика · кол-во ящиков = общее кол-во груш.
Общее кол-во груш : масса 1 ящика = кол-во ящиков.
Общее кол-во груш : кол-во ящиков = масса 1 ящика.
Оформляем условие в виде таблицы.

Рассуждаем.
На рынок привезли 48 кг слив в ящиках, по 8 кг в каждом. Значит, нам известно общее количество груш и масса 1 ящика, но неизвестно – сколько ящиков привезли. При этом из модели к задаче видно, что общее количество груш складывается из количества груш в каждом ящике. Поэтому, чтобы узнать, сколько ящиков привезли, нужно общее количество груш разделить на массу 1 ящика.
48 : 8 = 6 (ящ.) – слив привезли.
Продолжаем рассуждение.
Теперь мы знаем, что привезли 6 ящиков с грушами. В условии к задаче видно, что привезли столько же ящиков по 9 кг в каждом. Значит, теперь нам известно количество ящиков и масса 1 ящика, но неизвестно, сколько всего груш привезли.
При этом, общее количество груш складывается из количества груш в каждом из ящиков. Значит, чтобы узнать, сколько груш было привезено, нужно сложить количество груш в каждом из ящиков.
Но количество груш в каждом из ящиков одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 6 = 54 (кг) – груш привезли.
Записываем ответ.
Ответ: 54 кг груш привезли.
Решение выражением:
48 : 8 · 9 = 54 (кг), где 48 : 8 – количество груш в 1 ящике.
Номер 6.
Ответ:1) 0 : 9 = 0 0 : 24 = 0 0 ∙ 33 = 0

2)

1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Выполним деление и умножение.
0 : 9 = 0,
так как если 0 разделить на любое число, то получится 0.
0 : 24 = 0,
так как если 0 разделить на любое число, то получится 0.
0 · 33 = 0,
так как если 0 умножить на любое число, то получится 0.
Выполним вычисления по действиям.
1 2
(36 + 46) ∙ 0 = 0
В данном выражении присутствуют действия сложение и умножение, а также скобки. Вначале выполним действие в скобках – сложение, а потом действие вне скобок – умножение.
1) 35 + 46 = 81
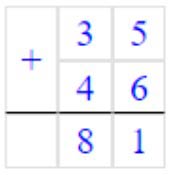
Складываем единицы. 5 + 6 = 11 – получилось 1 дес. и 1 ед.
Записываем в разряде единиц число 1, а 1 дес. запоминаем.
Складываем десятки. 3 + 4 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десяток.
Записываем в разряде десятков число 8.
Читаем ответ: 81.
2) 81 ∙ 0 = 0
При умножении любого числа на 0, получается 0.
1 2
(82 − 82) : 3 = 0
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 82 – 82 = 0
Если из числа вычесть само число, то получится нуль.
2) 0 : 3 = 0
При делении нуля на любое другое число, неравное 0, получается нуль.
1 2
(30 – 29) ∙ 8 = 8
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
1) 30 – 29 = 1
2) 1 ∙ 8 = 8
При умножении любого числа на 1 получается то число, которое умножали.
2 1 3
87 : (85 + 2) – 1 = 0
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действия в не скобок – деление, а потом вычитание.
1) 85 + 2 = 87
2) 87 : 87 = 1
Если число разделить на само себя, то получится 1.
3) 1 – 1 = 0
Если из числа вычесть само число, то получится нуль.
3 2 1
100 – 32 : (16 + 16) = 99
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действия в не скобок – деление, а потом вычитание.
1) 16 + 16 = 32
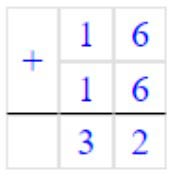
Складываем единицы. 6 + 6 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. 1 + 1 = 2 и ещё 1 дес., который запомнили 2 + 1 = 3 – получилось десяток.
Записываем в разряде десятков число 3.
Читаем ответ: 32.
2) 32 : 32 = 1
Если число разделить на само себя. то получится 1.
3) 100 – 1 = 99
3 1 2
90 – (48 – 18) ∙ 1 = 60
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 48 – 18 = (40 – 10) + (8 – 8) = 30 + 0 = 30
2) 30 ∙ 1 = 30
При умножении любого числа на 1 получается то число, которое умножали.
3) 90 – 30 = 60
Оформляем задание в тетрадь.
0 : 9 = 0
0 : 24 = 0
0 ∙ 33 = 0
(35 + 46) · 0 = 81 · 0 = 0
(82 – 82) : 3 = 0 : 3 = 0
(30 – 29) · 8 = 1 · 8 = 8
87 : (85 + 2) – 1 = 87 : 87 – 1 = 1 – 1 = 0
100 – 32 : (16 + 16) = 100 – 32 : 32 = 100 – 1 = 99
90 – (48 – 18) · 1 = 90 – 30 · 1 = 90 – 30 = 60
Расставляем порядок действий и выполняем вычисления.
3 1 2
60 – (16 – 9) · 4 = 32
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 16 – 9 = 16 – (6 + 3) = (16 – 6) – 3 = 10 – 3 = 7
2) 7 ∙ 4 = 28
3) 60 – 28 = 32
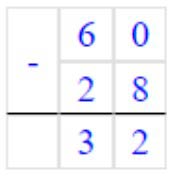
2 1 3
56 : (13 – 5) + 9 = 16
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – деление, а потом сложение.
1) 13 – 5 = 13 – (3 + 2) = (13 – 3) – 2 = 10 – 2 = 8
2) 56 : 8 = 7,так как 8 · 7 = 56
3) 7 + 9 = 7 + (3 + 6) = (7 + 3) + 6 = 10 + 6 = 16
2 1
42 + 72 : 9 = 50
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом действие сложение.
1) 72 : 9 = 8, так как 9 · 8 = 72
2) 42 + 8 = 40 + (2 + 8) = 40 + 10 = 50
2 1
60 – 54 : 6 = 51
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом действие вычитание.
1) 54 : 6 = 9, так как 6 · 9 = 54
2) 60 − 9 = (50 + 10) – 9 = 50 + (10 – 9) = 50 + 1 = 51
3 2 1
93 − 7 · (15 − 8) = 44
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 15 – 8 = 15 – (5 + 3) = (15 – 5) – 3 = 10 – 3 = 7
2) 7 ∙ 7 = 49
3) 93 – 49 = 93 – (43 + 6) = (93 – 43) – 6 = 50 – 6 = 44
1 3 2
8 · 9 + 64 : 8 = 80
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие– умножение и деление по порядку слева направо, а потом действие – сложение.
1) 8 ∙ 9 = 72
2) 64 : 8 = 8, так как 8 · 8 = 64
3) 72 + 8 = 70 + (2 + 8) = 70 + 10 = 80
Оформляем задание в тетрадь.
60 – (16 – 9) · 4 = 60 – 7 · 4 = 60 – 28 = 32
56 : (13 – 5) + 9 = 56 : 8 + 9 = 7 + 9 = 16
42 + 72 : 9 = 42 + 8 = 50
60 – 54 : 6 = 60 – 9 = 51
93 – 7 · (15 – 8 ) = 93 – 7 · 7 = 93 – 49 = 54
8 · 9 + 64 : 8 = 72 + 8 = 80
Номер 7.
Используя знаки умножения и деления, составь верные равенства с числами:
18, 24, 3, 8, 27, 9, 6, 2.
Ответ:
2 ∙ 3 = 6 6 ∙ 3 = 18 9 ∙ 2 = 18
6 : 3 = 2 18 : 6 = 3 18 : 2 = 9
6 : 2 = 3 18 : 3 = 6 18 : 9 = 2
3 ∙ 8 = 24 9 ∙ 3 = 27
24 : 8 = 3 27 : 9 = 3
24 : 3 = 8 27 : 3 = 9
Помни, что равенство – числовое выражение, составленное из чисел, знаков арифметических действий, скобок и знака равно.
Составим выражения со знаком умножение.
3 ∙ 2 = 6
2 ∙ 9 = 18
3 ∙ 8 = 24
3 ∙ 3 = 9
3∙ 9 = 27
3 ∙ 6 = 18
6 ∙ 3 = 18
Составим выражения со знаком деление.
6 : 2 = 3
6 : 3 = 2
18 : 9 = 2
18 : 2 = 9
24 : 3 = 8
24 : 8 = 3
9 : 3 = 3
27 : 3 = 9
27 : 9 = 3
18 : 3 = 6
18 : 6 = 3
Номер 8.
Реши уравнения с устным объяснением.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения.
Рассуждение.
х · 12 = 12
х – неизвестный множитель.
Чтобы найти неизвестный множитель нужно значение произведения разделить на известный множитель.
х : 9 = 0
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делитель.
25 : х = 25
х – неизвестный делитель.
Чтобы найти делитель, нужно делимое разделить на частное.
х : 9 = 1
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делитель.
Промежуточные вычисления и объяснения.
x ∙ 12 = 12
x = 12 : 12
x = 1
Значение произведения равно одному из множителей, это может быть в том случае если второй множитель равен 1.
x : 9 = 0
x = 9 ∙ 0
x = 0
Делитель равен 9, а значение частного равно 0, это может быть в том случае если делимое тоже равно 0.
25 : x = 25
x = 25 : 25
x = 1
Делимо и значение частного равны, это может быть в том случае если делили на 1.
x : 9 = 1
x = 1 ∙ 9
x = 9
Делитель равен 9, а значение частного равно1, это может быть в том случае если делимое и делитель равны.
Задание внизу страницы
Ответ:0 : 6 = 0 0 : 9 = 0 0 : 100 = 0
Чтобы понять, какие числа вписать в окошки проанализируй записи и подумай, при каких значениях чисел в квадратиках данные записи обращаются в верные равенства.
Рассуждение.
0 : 6 =
Делимое равно 0, а делитель – 6. При делении нуля на любое число , не равное 0, получается 0.
Записываем вместо окошка 0.
: 9 = 0
Делитель равен 9, а значение частного – 0. Делимое неизвестно, но из-за того, что значение частного равно 0, то вместо окошка ставим число 0, так как если 0 разделить на любое число, не равное 0, то получается 0.
0 : 100 =
Делимое равно 0, а делитель – 100. Чтобы понять, чему равно значение частного, нужно вспомнить, что при делении нуля на любое число, не равное нулю, получается нуль.
Записываем вместо окошка 0.
Оформляем задание в тетрадь.
0 : 6 = 0
0 : 9 = 0
0 : 100 = 0
Если 0 разделить на любое число, не равное нулю, то значение частного равно 0.
Номер 7.
Реши уравнения.
75 + x = 90 80 – k = 42 6 · n = 54
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действиями вычитания, сложения и умножения.
Рассуждаем.
75 + х = 90,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
80 – к = 42,
к – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
6 · n = 54,
n – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Решаем уравнения.
75 + x = 90
x = 90 − 75
x = 15
80 − k = 42
k = 80 − 42
k = 38
6 ∙ n = 54
n = 54 : 6
n = 9
Делаем проверку.
75 + х = 90
Проверка: вместо х подставим число 15.
75 + 15 = (70 + 10) + (5 + 5) = 80 + 10 = 90
90 = 90 – верно.
80 – k = 42
Проверка: вместо k подставим число 38.
80 – 38 = (70 + 10) – (30 + 8) = (70 – 30) + (10 – 8) = 40 + 2 = 42
42 = 42 – верно.
6 · n = 54
Проверка: вместо n подставим число 9.
6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
54 = 54 – верно.
Номер 8.
1) Найди площадь прямоугольника BCKE и площадь прямоугольника AEKD 2) Найди площадь прямоугольника ABCD.Сколькими способами это можно сделать?

1) Площадь BCKE: BC · BE = 2 · 2 = 4 (см2) Площадь AEKD: АЕ · DA = 3 · 2 = 6 (см2) 2) Площадь BCDA: 1 способ: Измеряем стороны прямоугольника BCDA: BC = 2 см CD = 5 см Площадь BCDA: BC · CD = 2 · 5 = 10(см2) 2 способ: Складываю площади прямоугольников BCKE и AEKD, значит, площадь DCDA: 4 + 6 = 10 (см2)
Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
С помощью линейки измерим стороны.
В прямоугольнике ВСКЕ все стороны равны:
ВС = ЕК = СК = ВЕ = 2 см
В прямоугольнике ЕКDA стороны попарно равны:
КD = EA = 3 см
КЕ = AD = 2 см
Вычислим площади фигур.
ВСКЕ – квадрат, так как у него все сторны равны. Чтобы вычислить площадь квадрата нужно длину умножить на ширину.
2 · 2 = 4 (см2) – площадь ВСКЕ
ЕКDA – прямоугольник. Чтобы вычислить площадь прямоугольника нужно длину умножить на ширину.
2 · 3 = 6 (см2) – площадь ЕКDA
Записываем ответ.
Ответ: 4 см2 и 6 см2.
Узнаем длину ширины и длины.
СВ = DA = 2 см
CD = BE = 2 см + 3 см = 5 см
Вычислим площадь ABCD.
Вычислить площадь АВСD можно двумя способами:
1) Площадь АВСD равна сумме площадей фигур ВСКЕ и ЕКDA. Значит, чтобы узнать, чему арвна площадь нужно площади двух фигур сложить:
4 + 6 = 10 (см2) – площадь АВСD
2) Чтобы вычислить площадь прямоугольника нужно длину умножить на ширину.
2 · 5 = 10 (см2) – площадь АВСD
Записываем ответ.
Ответ: 10 см2.
Номер 9.
1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной OK (рис. 1); с общей стороной NP (рис. 2). 2) Узнай, площадь какой фигуры меньше: прямоугольника BCKE или треугольника OKD – и на сколько квадратных сантиметров.

1) Площадь OKD = 3 см2
Площадь OKEA = 9 см2
Площадь NPLS = 9 см2
Площадь NPT = 3 см2
2) Площадь BCKE = 4 см2
Площадь OKD = 3 см2
4 см2 > 3 см2 на 1 см2
ПОДРОБНО:
Задание 1. Фигуры с общей стороной OK: треугольник OKD и четырёхугольник OKEA.
Площадь OKD = (OD · KD) : 22 · 3 : 2 = 6 : 2 = 3см2
Площадь OKEA = EKDA – OKD4 · 3 – 3 = 12 – 3 = 9 см2
Фигуры с общей стороной NP:
треугольник NPS, квадрат NPLS, треугольник NPT и прямоугольник NPTM.
Площадь квадрата NPLS = NP · LS3 · 3 = 9 см2
Площадь NPS = NPLS :
2Площадь NPTM = NP · NM3 · 2 = 6 см2
Площадь NPT = NPTM : 26 : 2 = 3 см2
Задание 2. Площадь BCKE = BC · CK4 · 1 = 4 см2
Площадь OKD = (OD · KD) : 22 · 3 : 2 = 6 : 2 = 3 см2
Площадь OKD меньше площади BCKE. 4 – 3 = 1 см2
Ответ: Площадь OKD меньше площади BCKE на 1 см2.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Но у фигур сложных, т.е. у которых площадь нельзя вычислить по формуле, нужно поступать иначе. У сложных фигур площадь фигуры равна сумме площадей фигур, из которых она состоит.
Начертим рисунок 1.
-(2023).jpg)
Общая сторона OK есть у трёх фигур:
треугольника OKD,
четырехугольника OKEA,
пятиугольника OKCBA.
Измерим нужные стороны этих фигур (2 клетки = 1 см)
ОD = 2 см
КD = 3 см
ЕК = 4 см
ВС = 4 см
СD = 4 см
Вычислим площади фигур.
Треугольника ОКD в 2 раза меньше прямоугольника со сторонами 3 см и 2 см, значит и площадь треугольника в 2 раза меньше площади прямоугольника.
Найдём площадь прямоугольника со сторонами 3 см и 2 см.
3 см · 2 см = 6 (см2) – площадь прямоугольника.
Теперь найдём площадь треугольника, разделим площадь прямоугольника на 2:
6 см2 : 2 = 3 см2 – площадь треугольника OKD.
Площадь четырехугольника ОКЕА меньше площади прямоугольника ЕКDА на площадь треугольника ОКD. Значит, чтобы найти площадь четырёхугольника ОКЕА нужно из площади прямоугольника ЕКDA вычесть площадь треугольника ОКD.
Найдём площадь ЕКDA:
ЕК ∙ КD = 4 см ∙ 3 см = 12 см2 – площадь ЕКDА
Найдём площадь ОКЕА, зная что площадь треугольника ОКD равна 3 см2
12 см2 – 3 см2 = 9 см2 – площадь ОКЕА
Площадь ОКСВА состоит из площади фигур прямоугольника ЕВСК и четырёхугольника ОКЕА. Значит, чтобы узнать площадь фигуры ОКСВА нужно сложить площади фигур ЕВСК и ОКЕА.
Найдём площадь ЕВСК:
ЕВ = 1 см и ВС = 4 см.
1 · 4 = 4 (см2) – площадь ЕВСК.
Найдём площадь ОКСВА, зная что площадь ОКЕА равна 9
4 + 9 = 13 (см2) – полощадь ОКСВА
Записываем ответ.
Ответ: 3 см2 – площадь треугольника OKD; 9 см2 – площадь ОКЕА; 13 (см2) – полощадь ОКСВА.
Начертим фигуру 2.
-(2023).jpg)
Вычислим площади фигур.
Общая сторона NP есть у четырёх фигур:
треугольника NPS,
квадрата NPLS,
треугольника NPT,
прямоугольника NPTM.
Измерим нужные стороны этих фигур (2 клетки = 1 см)
NP = 3 см
NS = 3 см
РТ = 2 см
ТМ = 3 см
Площадь NPLS можно вычислить, умножив длину на ширину:
NP ∙ NS = 3 см ∙ 3 см = 9 см2 – площадь NPLS
Площадь треугольника NPS в 2 раза меньше прямоугольника со сторонами 3 см и 3 см, то есть площади NPLS.
3 см · 3 см = 9 см2 = 900 мм2 – площадь прямоугольника со сторонами 3 см.
так как 1 см2 = 10 мм ∙ 10 мм = 100 мм2
9 см2 : 2 = 900 мм2 : 2 = 450 мм2 – площадь треугольника NPS.
Площадь NPTM можно вычислить, умножив длину на ширину:
ТМ ∙ РТ = 3 см ∙ 2 см = 6 см2 – площадь NPTM
Площадь треугольника NPT в 2 раза меньше площади NPTM.
6 см2 : 2 = 3 см2 – площадь NPT
Записываем ответ.
Ответ: 9 см2 – площадь NPLS, 450 мм2 – площадь треугольника NPS, 6 см2 – площадь NPTM, 3 см2 – площадь NPT.
Вычислим площади фигур.
Чтобы сказать, площадь какой фигуры меньше, нужно вначале вычислить площади фигур.
ВСКЕ – прямоугольник. Чтобы найти его площадь нужно длину умножить на ширину.
ВЕ = 1 см
ВС = 4 см
1 · 4 = 4 (см2) – площадь ВСКЕ
ОКD – треугольник, он в два раза меньше прямоугольника со сторонами 3 см и 2 см. Значит и площадь будет в два раза меньше.
Найдём площадь прямоугольника со сторонами 3 см и 2 см.
3 см · 2 см = 6 (см2) – площадь прямоугольника.
Теперь найдём площадь треугольника, разделив площадь прямоугольника на 2:
6 см2 : 2 = 3 см2 – площадь треугольника OKD.
Сравним площади фигур.
Площадь ВСКЕ = 4 см2
Площадь треугольника OKD = 3 см2
4 см2 > 3 см2
Значит площадь треугольника ОКD меньше площади прямоугольника ВСКЕ.
Чтобы узнать на сколько одна площадь меньше другой, нужно из большей площади вычесть меньшую площадь:
4 – 3 = 1 (см2) – на сколько площадь треугольника ОКD меньше площади прмяугольника ВСКЕ.
Записываем ответ.
Ответ: площадь треугольника ОКD ментше площади прямуогогльника ВСКЕ на 1 см2.
Задание внизу страницы.
На сколько 9 меньше, чем 72? Во сколько раз 6 меньше, чем 54?
Ответ:
9 меньше чем 72 на 63. потому что 72 - 9 = 63
6 меньше чем 54 в 9 раз, потому что 54 : 6 = 9
1) Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
2) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
Рассуждаем.
72 – 9 = 72 – (2 + 7) = (72 – 2) – 7 = 70 – 7 = 63
Число 9 представим в виде суммы числе 2 и 7. Из числа 72 вначале вычтем число 2, а потом вычтем число 7.
54 : 6 = 9, так как 6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
1) 72 − 9 = 63 – на сколько число 9 меньше, чем 72.
2) 54 : 6 = 9 (раз) – во сколько раз число 6 меньше, чем 54.
Задание на полях страницы.

54 : 9 = 6 6 · 7 = 42 42 + 58 = 100 100 – 75 = 25
1) Выполни действия по порядку.
2) Первая зеленая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
54 : 9 = 6, так как 9 · 6 = 54, где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
42 + 58 = (40 + 50) + (2 + 8) = 90 + 10 = 100
Складываем по разрядам: единицы складываем с единицами, а десятки - с десятками.
100 – 75 = 25
.jpg)
Оформляем задание в тетрадь.
54 : 9 = 6
6 ∙ 7 = 42
42 + 58 = 100
100 – 75 = 25
54 : 9 = 6 → 6 · 7 = 42 → 42 + 58 = 100 → 100 - 75 = 25
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.