Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 83

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Умножение на 0
Номер 1.
Реши с устным объяснением.
Ответ:4 ∙ 0 = 0 7 + 0 = 7 9 ∙ 1 = 9 1 ∙ 9 = 9 0 ∙ 9 = 0 9 − 0 = 9
1) Помни при умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число. Правила уменьшения и увеличения числа на 0.
Устные рассуждения.
7 · 0 = 0,
где 7 – одинаковое слагаемое, а 0 – количество одинаковых слагаемых.
При умножении любого числа на нуль получается нуль.
7 + 0 = 7,
значит число 7 увеличивают на 0 единиц и получают число, которое увеличивали.
9 · 1 = 9,
где 9 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых, значит число 9 повторяют 1 раз и получают число, которое умножали на единицу.
При умножении любого числа на 1, получается число, которое умножали.
1 · 9 = 9 · 1 = 9,
где 9 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых, значит число 9 повторяют 1 раз и получают число, которое умножали на единицу.
При умножении любого числа на 1, получается число, которое умножали.
0 · 9 = 0,
так как число 0 умножают на 9, значит повторяют 9 раз, а если 0 умножить на любое число, то получится 0.
При умножении любого числа на нуль получается нуль.
9 – 0 = 9,
так как число 9 уменьшили на 0, значит вычли 0 единиц, и получили число, которое уменьшали.
Оформляем задание в тетрадь.
4 ∙ 0 = 0
Если любое число умножить на 0, то произведение равно 0.
7 + 0 = 7
Если к любому числу прибавить 0, то число не изменится.
9 ∙ 1 = 9
Если число умножить на 1, то число не изменится.
1 ∙ 9 = 9
Если число умножить на 1, то число не изменится.
0 ∙ 9 = 0
Если число умножить на 0, то произведение равно 0.
9 – 0 = 9
Если из числа вычесть 0, то число не изменится.
Номер 2.
Ответ:18 ∙ 0 = 0 6 ∙ 0 = 0 12 ∙ 0 = 0 0 ∙ 19 = 0 8 ∙ 1 = 8 12 − 0 = 12

1) Помни при умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
3) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
4) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
5) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним умножение.
18 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
0 · 19 = 0,
так как если 0 умножить на любое число, но получится 0.
6 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
8 · 1 = 8,
где 8 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых, значит 8 берут по 1 разу и получают это же число.
12 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
Выполним вычитание.
12 – 0 = 12,
так как если из любого числа вычесть 0, значит уменьшить число на 0 единиц, то получится это же число.
Выполним вычисления по действиям.
1 2
72 : 9 ∙ 0 = 0
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 72 : 9 = 8, так как 9 · 8 = 72
2) 8 ∙ 0 = 0
1 2
1 ∙ 49 : 7 = 7
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 1 ∙ 49 = 49
2) 49 : 7 = 7, так как 7 · 7 = 49
1 2
(6 : 6) ∙ 9 = 9
В данном выражении присутствуют действия умножение и деление, а также скобки. Выполняем вначале действие в скобках – деление, а потом действие вне скобок – умножение.
1) 6 : 6 = 1, так как 6 · 1 = 6
2) 1 ∙ 9 = 9
2 1
8 ∙ (5 – 5) = 0
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Выполняем вначале действие в скобках – вычитание, а потом действие вне скобок – умножение.
1) 5 – 5 = 0
2) 8 ∙ 0 = 0
Оформляем задание в тетрадь.
18 ∙ 0 = 0
0 ∙ 19 = 0
6 ∙ 0 = 0
8 ∙ 1 = 8
12 ∙ 0 = 0
12 − 0 = 12
72 : 9 · 0 = 8 · 0 = 0
1 · 49 : 7 = 49 : 7 = 7
(6 : 6) · 9 = 1 · 9 = 9
8 · (5 – 5) = 8 · 0 = 0
Номер 3.
Купили 35 м обоев в рулонах, по 7 м в каждом, и столько же рулонов, по 10 м в каждом. Сколько метров обоев было в рулонах по 10 м?
Ответ:
1-й способ решения: 1) 35 : 7 = 5 (р.) – было по 7 метров. 2) 5 ∙ 10 = 50 (м) обоев было в 10 рулонах Ответ: 50 м было в рулонах по 10 м.
2-й способ решения: 35 : 7 ∙ 10 = 5 ∙ 10 = 50 (м) – было по 10 м. Ответ: 50 м.
Данная задача: вида «кол-во обоев в 1 рулоне, кол-во рулонов, общее кол-во обоев» характеризуется зависимостями между компонентами:
Кол-во обоев в 1 рулоне · кол-во рулонов = общее кол-во обоев.
Общее кол-во обоев : кол-во рулонов = кол-во обоев в 1 рулоне.
Общее кол-во обоев : кол-во обоев в 1 рулоне = кол-во рулонов.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество обоев складывается из количества обоев в каждом рулоне. Значит, чтобы узнать, сколько рулонов купили, нужно общее количество рулонов разделить на количество обоев в 1 рулоне.
35 : 7 = 5 (р.) – было по 7 метров.
Продолжаем рассуждение.
Общее количество купленных обоев складывается из количества обоев в каждом рулоне.
Значит, чтобы узнать, сколько обоев купили всего, нужно сложить количество обоев каждого рулона.
Но количество обоев в 1 рулоне одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.
5 ∙ 10 = 50 (м) – было по 10 м.
Записываем ответ.
Ответ: 50 м было в руках по 10 м.
Решение выражением:
10 · (35 : 7) = 50 (м), где 35 : 7 – количество обоев в 1 рулоне.
Номер 4.
В школьном оркестре 7 девочек, а мальчиков в 4 раза больше, чем девочек. Сколько всего детей в школьном оркестре? На сколько больше мальчиков в этом оркестре, чем девочек?
Ответ:
1) 7 ∙ 4 = 28 (чел.) – мальчиков. 2) 28 + 7 = 35 (чел.) – всего. 3) 28 − 7 = 21 (чел.) больше мальчиков, чем девочек Ответ: на 21 ребёнка больше мальчиков, чем девочек; всего 35 человек.
1) «в 4 раза больше», значит, вычисляется умножением.
2) «всего», значит, вычисляется сложением.
3) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Вычисляется вычитанием.
Оформляем условие в виде краткой записи.
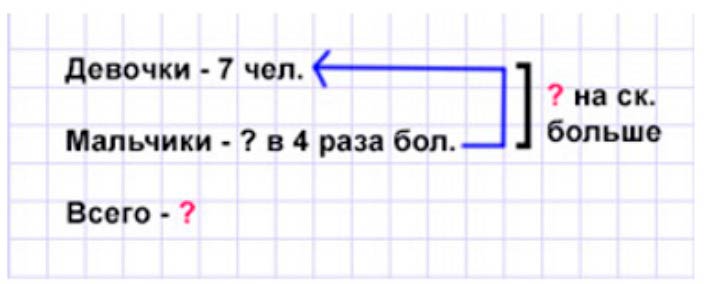
Рассуждаем.
В школьном оркестре 7 девочек, а мальчиков – в 4 раза больше, чем девочек. Значит, чтобы узнать, сколько мальчиков в школьном оркестре, нужно количество девочек умножить на 6.
7 ∙ 4 = 28 (чел.) – мальчиков.
Продолжаем рассуждение.
Общее количество детей в школьном оркестре складывается из количества мальчиков и девочек. Значит, чтобы узнать, сколько в хоре детей, нужно сложить количество мальчиков и девочек.
28 + 7 = 35 (чел.) – всего детей в оркестре.
Продолжаем рассуждение.
В школьном оркестре 7 девочек, а мальчиков – 28.
Чтобы узнать, на сколько больше в оркестре мальчиков, чем девочек, нужно из количества мальчиков вычесть количество девочек.
28 − 7 = 21 (чел.) – на сколько больше.
Записываем ответ.
Ответ: на 21 ребёнка больше мальчиков, чем девочек; всего 35 человек.
Решение выражением:
1) 7 · 4 – 7 = 21 (чел.) – на сколько мальчиков больше, чем девочек;
2) 7 · 4 + 7 = 35 (чел.) – всего детей в оркестре;
где 7 · 4 – количество мальчиков в оркестре.
Номер 5.
Ответ:8 см = 80 мм 8 см 4 мм = 84 мм 5 м = 50 дм 8 дм 7 см = 87 см 6 дм = 60 см 2 м 4 дм = 24 дм
Вспомни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 100 см
1 м = 10 дм
Устные рассуждения.
8 см = 8 · 10 мм = 80 мм,
так как 1 см = 10 мм
5 м = 5 · 10 мм = 50 дм,
так как 1 м = 10 дм
6 дм = 6 · 10 см = 60 см,
так как 1 дм = 10 см
8 см 4 мм = 8 · 10 мм + 4 мм = 80 см + 4 мм = 84 мм,
так как 1 см = 10 мм
8 дм 7 см = 8 · 10 см + 7 см = 80 см + 7 см = 87 см,
так как 1 дм = 10 см
2 м 4 дм = 2 · 10 дм + 4 дм = 20 дм + 4 дм = 24 дм,
так как 1 м = 10 дм
Оформляем задание в тетрадь.
8 см = 80 мм
5 м = 50 дм
6 дм = 60 см
8 см 4 мм = 80 мм + 4 мм = 84 мм
8 дм 7 см = 80 см+ 7 см = 87 см
2 м 4 дм = 20 дм + 4дм = 24 дм
Номер 6.
Ответ:9 ∙ 6 = 54 49 : 7 = 7

1) Помни при умножении любого числа на 1, получается число, которое умножали. Существует еще и другие: умножение числа на 0, и 0 на любое число.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем умножение и деление.
9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
49 : 7 = 7, так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполняем вычисления по действиям.
1 2
(72 − 56) : 4 = 4
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 72 – 56 = 16
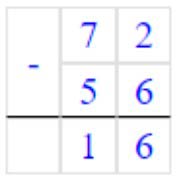
Вычитаем единицы. От числа 2 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 + 2 = 12 ед., 12 – 6 = 6 – получилось единиц.
Записываем в разряде единиц число 6.
Вычитаем десятки. Было 7 дес., мы занимали 1 дес, осталось 7 – 1 = 6 дес.,
6 – 5 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 16.
2) 16 : 4 = 4, так как 4 · 4 = 16
1 2
(63 – 15) : 8 = 6
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 63 – 15 = 48
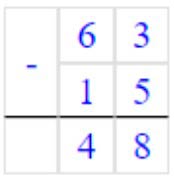
Вычитаем единицы. От числа 3 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 + 3 = 13 ед., 13 – 5 = 8 – получилось единиц.
Записываем в разряде единиц число 8.
Вычитаем десятки. Было 6 дес., мы занимали 1 дес, осталось 6 – 1 = 5 дес.,
5 – 1 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 48.
2) 48 : 8 = 6, так как 8 · 6 = 48
2 1 3
100 – 3 · 7 + 1 = 80
В данном выражении присутствуют действия сложение, вычитание и умножение. Вначале выполняем действие умножение, потом - вычитание и последним действием – сложение.
1) 3 ∙ 7 = 21
2) 100 – 21 = 79
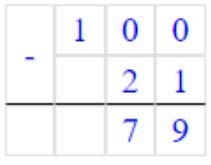
Вычитаем единицы. От числа 0 мы не можем отнять 1.
Занимаем 1 дес. = 10 ед., 10 – 1 = 9 – получилось единиц.
Записываем в разряде единиц число 9.
Вычитаем десятки. 1 сот. = 10 ед. Было 10 дес., мы занимали 1 дес, осталось 10 – 1 = 9 дес., 9 – 2 = 7 – получилось десятков.
Записываем в разряде десятков число 7.
Читаем ответ: 79.
3) 79 + 1 = 80
3 1 2
100 – 42 : 6 ∙ 5 = 65
В данном выражении присутствуют действия вычитание, умножение и деление. Вначале выполняем действие деление, потом - умножение и последним действием – вычитание.
1) 42 : 6 = 7, так как 6 · 7 = 42
2) 7 ∙ 5 = 35
3) 100 – 35 = 65
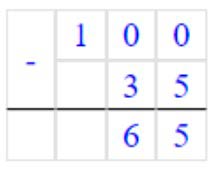
Вычитаем единицы. От числа 0 мы не можем отнять 1.
Занимаем 1 дес. = 10 ед., 10 – 5 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Вычитаем десятки. 1 сот. = 10 ед. Было 10 дес., мы занимали 1 дес, осталось 10 – 1 = 9 дес., 9 – 3 = 6 – получилось десятков.
Записываем в разряде десятков число 6.
Читаем ответ: 65.
Оформляем задание в тетрадь.
9 · 6 = 54
49 : 7 = 7
(72 – 56) : 4 = 16 : 4 = 4
(63 – 15) : 8 = 8 : 8 = 1
100 – 3 · 7 + 1 = 100 – 21 + 1 = 79 + 1 = 80
100 – 42 : 6 · 5 = 100 – 7 · 5 = 100 – 35 = 65
Номер 7.
Реши уравнения.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения, а также умножением и делением.
Рассмотрим уравнения.
80 : х = 8,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
32 : х = 4,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
х : 8 = 8,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
х · 3 = 21,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х + 29 = 80,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х – 2 = 40,
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
Решим уравнение.
80 : x = 8
x = 80 : 8
x = 10
32 : x = 4
x = 32 : 4
x = 8
x : 8 = 8
x = 8 ∙ 8
x = 64
x ∙ 3 = 21
x = 21 : 3
x = 7
x + 29 = 80
x = 80 − 29
x = 51
x − 2 = 40
x = 40 + 2
x = 42
Делаем проверку.
80 : x = 8
Проверка: вместо неизвестно подставим число 10.
80 : 10 = 8, так как 8 · 10 = 80
8 = 8 – верно.
32 : x = 4
Проверка: вместо неизвестно подставим число 8.
32 : 8 = 4, так как 8 · 4 = 32
4 = 4 – верно.
x : 8 = 8
Проверка: вместо неизвестно подставим число 64.
64 : 8 = 8 , так как 8 · 8 = 64
8 = 8 – верно.
x ∙ 3 = 21
Проверка: вместо неизвестно подставим число 7.
7 · 3 = 21
21 = 21 – верно.
x + 29 = 80
Проверка: вместо неизвестно подставим число 51.
51 + 29 = (50 + 20) + (1 + 9) = 70 + 10 = 80
80 = 80 – верно.
x − 2 = 40
Проверка: вместо неизвестно подставим число 42.
42 – 2 = 40 + (2 – 2) = 40
40 = 40 – верно.
Номер 8.
Как переложить 3 палочки, чтобы получилось 4 маленьких одинаковых квадрата и 1 большой?


Для того, чтобы выполнить задание, удобнее провести реальные действия с предметами, например, со спичками.
Рассмотрим.
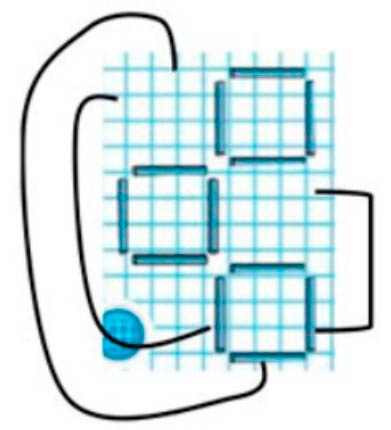
Нужно три палочки из 3 квадрата переместить как показано на рисунке.
Рассуждаем.
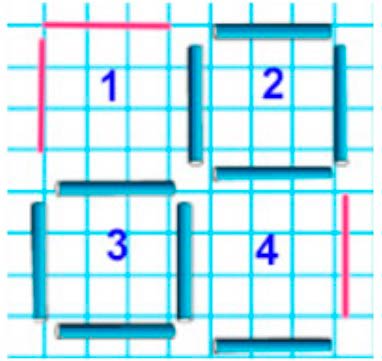
Получилось 4 маленьких квадрата и один большой квадрат.
Задание внизу страницы
Ответ:15 ∙ 1 = 15 14 + 0 = 14 0 ∙ 34 = 0 15 ∙ 0 = 0 18 ‒ 18 = 0 0 ∙ 17 = 0
Чтобы выполнить задание не обязательно выполнять вычисления, достаточно проанализировать записи, а проверить себя – арифметически, т.е. выполнив действия.
Рассуждаем.
15 · = 15
Данное равенство основано на действии умножение. При этом, первый можитель равен занчению произведения. Такое возможно, если число умножили на 1, то есть увеличили в 1 раз.
Вместо окошка запишем число 1.
15 · = 0
Данное равенство основано на действии умножение. При этом первый множитель равен 15, а произвдение 0. Такое возможно если один из множителей равен 0.
Вместо окошка запишем число 0.
14 + = 14
Данное равенство основано на действии сложение. При этом первое слагаемое равно сумме. Такое возможно если число увеличили на 0, то есть прибавили 0.
Вместо окошка запишем число 0.
18 - = 0
Данное равенство основано на действии вычитании. При этом уменьшаеоме равно 18, а значение разности равно 0. Такое возможно если из числа вычитали само число.
Вместо окошка запишем число 18.
· 34 = 0
Данное равенство основано на действии умножение. При этом второй множитель равен 34, а произвдение 0. Такое возможно если один из множителей равен 0.
Вместо окошка запишем число 0.
· 17 = 0
Данное равенство основано на действии умножение. При этом первый множитель равен 17, а произвдение 0. Такое возможно если один из множителей равен 0.
Вместо окошка запишем число 0.
Делаем проверку.
15 · 1 = 15
При умножении любого числа на 1 получается то число, которое умножали.
15 · 0 = 0
При умножении любого числа на нуль получается нуль.
14 + 0 = 14
Если к числу прибавить нуль, то число не изменится.
18 – 18 = 0
Если из числа вычесть само число, то получится нуль.
0 · 34 = 0
При умножении любого числа на нуль получается нуль.
0 · 17 = 0
При умножении любого числа на нуль получается нуль.
Оформляем задание в тетрадь.
15 ∙ 1 = 15
15 ∙ 0 = 0
14 + 0 = 14
18 − 18 = 0
0 ∙ 34 = 0
0 ∙ 17 = 0
Деление нуля на число
Ты знаешь, что 0 · b = 0, поэтому если произведение 0 разделить на b (при этом b не равно 0), то получим 0. Например: 0 : 8 = 0, так как 0 · 8 = 0; 0 : 3 = 0, так как 0 · 3 = 0.
Номер 1.
Реши с устным объяснением.
4 · 6 1 · 8 0 · 4 6 · 4 8 · 1 4 · 0 24 : 6 8 : 8 0 : 4 24 : 4 8 : 1 0 : 8
Ответ:4 ∙ 6 = 24 1 ∙ 8 = 8 0 ∙ 4 = 0 6 ∙ 4 = 24 8 ∙ 1 = 8 4 ∙ 0 = 0 24 : 6 = 4 8 : 8 = 1 0 : 4 = 0 24 : 4 = 6 8 : 1 = 8 0 : 8 = 0
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Выполним умножение.
4 · 6 = 24, где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 4 = 24, где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Выполним деление.
24 : 6 = 4, так как 6 · 4 = 24, где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
24 : 4 = 6, так как 4 · 6 = 24, где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Выполним умножение и деление на 1.
1 · 8 = 8, так как если 1 умножить на любое число, то получится это же число.
8 · 1 = 8, так как если любое число умножить на единицу, то получится число, которое умножали.
8 : 8 = 1, так как если любое число разделить на само себя, то получится единица.
8 : 1 = 8, так как если любое число разделить на 1, то получится число, которое делили.
Выполним умножение и деление на 0.
0 · 4 = 0, так как если 0 умножить на любое число, то получится число, на которое умножали.
4 · 0 = 0, так как если любое число умножить на 0, то получится 0.
0 : 4 = 0, так как если 0 разделить на любое число, то получится 0.
0 : 8 = 0, так как если 0 разделить на любое число, то получится 0.
Оформим задание в тетрадь.
4 ∙ 6 = 24
6 ∙ 4 = 24
24 : 6 = 4
24 : 4 = 6
1 ∙ 8 = 8
8 ∙ 1 = 8
8 : 8 = 1
8 : 1 = 8
0 ∙ 4 = 0
4 ∙ 0 = 0
0 : 4 = 0
0 : 8 = 0
Номер 2.
Закончи вывод и приведи свои примеры.
При делении нуля на любое другое число, не равное 0, получается ... .
При делении нуля на любое другое число, не равное 0, получается нуль. 0 : 17 = 0 0 : 5 = 0 0 : 7 = 0.
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Продолжим фразу.
При делении нуля на любое другое число, не равное 0, получается 0.
Приведём примеры.
0 : 17 = 0,
0 : 5 = 0,
0 : 7 = 0.
Если произведение 0 разделить на b (при этом b неравно 0), то получим 0.
Номер 3.
1) Запиши названия всех треугольников, имеющих: общую вершину — точку А; общую сторону — отрезок АМ.
2) Запиши названия всех четырёхугольников.

1) Общая вершина A – ABK. ABC. ABN, CAN, AND, AMD, ABD, AKM.
Общая сторона – отрезок АМ: AMB, AMD, AMK.
2) KCNМ, DKСN, ACND, ABND.
1) Треугольник – геометрическая фигура, у которой 3 угла, 3 вершины и 3 стороны.
2) Четырехугольник – геометрическая фигура, у которой 4 угла и 4 стороны.
Рассуждаем.
Треугольники, имеющие общую вершину − точку A:
ΔABC, ΔABD, ΔABK, ΔABM, ΔABN, ΔACN, ΔADK, ΔADM, ΔADN, ΔAKM.
Проилюстрируем.
-(2023).jpg)
Продолжаем рассуждение.
Треугольники, имеющие общую сторону − отрезок AM:
ΔAMB, ΔAMD, ΔAMK.
Проилюстрируем.
-(2023).jpg)
Выполняем задание 2.
Четырехугольники: ABND, ACND, MKCN, DKCN.
Проилюстрируем.
-(2023).jpg)
Номер 4.
У Юры 3 монеты по 10 р. и ещё несколько рублей. Сможет ли он на эти деньги купить 7 одинаковых по цене тетрадей? Какие дополнительные данные нужны? Введи их, сделай вывод и подтверди его вычислениями.
Ответ:
1) Нужно знать, сколько еще денег было у Юры
2) Нужно знать стоимость тетрадей
1 Способ
У Юры еще 6 рублей. Стоимость тетради 5 рубля.
1) 3 · 10 + 6 = 36 (р) – всего у Юры
2) 7 · 5 = 35 (р) – стоимость тетрадей
3) 36р > 35 р , сможет купить
2 способ
У Юры еще 6 рублей. Стоимость тетради 7 рубля.
1) 3 · 10 + 6 = 36 (р) – всего у Юры
2) 7 · 7 = 49 (р) – стоимость тетрадей
36р < 49р, не сможет купить
Данная задача: вида «номинал одной монеты, количество монет, общее количество денег» характеризуется зависимостями между компонентами:
Номинал 1 монеты · кол-во монет = общее кол-во денег.
Общее кол-во денег : номинал 1 монеты = кол-во монет.
Общее кол-во денег : кол-во монет = номинал 1 монеты.
Укажем недостающие данные.
1) Нужно знать, сколько еще денег было у Юры.
У Юры еще 6 рублей. Стоимость тетради 5 рубля.
2) Нужно знать стоимость тетрадей.
У Юры еще 6 рублей. Стоимость тетради 7 рубля.
Решим задачу первым способом.
1) 3 · 10 + 6 = 36 (р) — всего у Юры.
2) 7 · 5 = 35 (р) — стоимость тетрадей.
3) 36р > 35 р , сможет купить.
Решим задачу вторым способом.
1) 3 · 10 + 6 = 36 (р) — всего у Юры.
2) 7 · 7 = 49 (р) — стоимость тетрадей.
3) 36р < 49р, не сможет купить.
Номер 5.
На рынок привезли 48 кг слив в ящиках, по 8 кг в каждом, и столько же ящиков груш, по 9 кг. Сколько килограммов груш привезли?
Ответ:.jpg)
1) 48 : 8 = 6 (ящ.) – слив привезли.
2) 9 ∙ 6 = 54 (кг) груш всего
Ответ: 54 кг груш привезли.
Данная задача: вида «масса 1 ящика, кол-во ящиков, общее кол-во груш» характеризуется зависимостями между компонентами:
Масса 1 ящика · кол-во ящиков = общее кол-во груш.
Общее кол-во груш : масса 1 ящика = кол-во ящиков.
Общее кол-во груш : кол-во ящиков = масса 1 ящика.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
На рынок привезли 48 кг слив в ящиках, по 8 кг в каждом. Значит, нам известно общее количество груш и масса 1 ящика, но неизвестно – сколько ящиков привезли. При этом из модели к задаче видно, что общее количество груш складывается из количества груш в каждом ящике. Поэтому, чтобы узнать, сколько ящиков привезли, нужно общее количество груш разделить на массу 1 ящика.
48 : 8 = 6 (ящ.) – слив привезли.
Продолжаем рассуждение.
Теперь мы знаем, что привезли 6 ящиков с грушами. В условии к задаче видно, что привезли столько же ящиков по 9 кг в каждом. Значит, теперь нам известно количество ящиков и масса 1 ящика, но неизвестно, сколько всего груш привезли.
При этом, общее количество груш складывается из количества груш в каждом из ящиков. Значит, чтобы узнать, сколько груш было привезено, нужно сложить количество груш в каждом из ящиков.
Но количество груш в каждом из ящиков одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 6 = 54 (кг) – груш привезли.
Записываем ответ.
Ответ: 54 кг груш привезли.
Решение выражением: 48 : 8 · 9 = 54 (кг), где 48 : 8 – количество груш в 1 ящике.
Номер 6.
1) 0 : 9 (35 + 46) · 0 87 : (85 + 2) – 1
0 : 24 (82 – 82) : 3 100 – 32 : (16 + 16)
0 · 33 (30 – 29) · 8 90 – (48 – 18) · 1
2) 60 – (16 – 9) · 4 42 + 72 : 9 93 – 7 · (15 – 8)
56 : (13 – 5) + 9 60 – 54 : 6 8 · 9 + 64 : 8
1) 0 : 9 = 0 0 : 24 = 0 0 ∙ 33 = 0

1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Выполним деление и умножение.
0 : 9 = 0, так как если 0 разделить на любое число, то получится 0.
0 : 24 = 0, так как если 0 разделить на любое число, то получится 0.
0 · 33 = 0, так как если 0 умножить на любое число, то получится 0.
Выполним вычисления по действиям.
1 2
(35 + 46) · 0 = 0
В данном выражении присутствуют действия сложение и умножение, а также скобки. Вначале выполним действие в скобках – сложение, а потом действие вне скобок – умножение.
1) 35 + 46 = 81
-(2023).jpg)
Складываем единицы. 5 + 6 = 11 – получилось 1 дес. и 1 ед.
Записываем в разряде единиц число 1, а 1 дес. запоминаем.
Складываем десятки. 3 + 4 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десяток.
Записываем в разряде десятков число 8.
Читаем ответ: 81.
2) 81 ∙ 0 = 0
При умножении любого числа на 0, получается 0.
1 2
(82 − 82) : 3 = 0
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 82 – 82 = 0
Если из числа вычесть само число, то получится нуль.
2) 0 : 3 = 0
При делении нуля на любое другое число, неравное 0, получается нуль.
1 2
(30 − 29) ∙ 8 = 8
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
1) 30 – 29 = 1
2) 1 ∙ 8 = 8
При умножении любого числа на 1 получается то число, которое умножали.
2 1 3
87 : (85 + 2) − 1 = 0
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действия в не скобок – деление, а потом вычитание.
1) 85 + 2 = 87
2) 87 : 87 = 1
Если число разделить на само себя, то получится 1.
3) 1 – 1 = 0
Если из числа вычесть само число, то получится нуль.
3 2 1
100 – 32 : (16 + 16) = 99
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действия в не скобок – деление, а потом вычитание.
1) 16 + 16 = 32
-(2023).jpg)
Складываем единицы. 6 + 6 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. 1 + 1 = 2 и ещё 1 дес., который запомнили 2 + 1 = 3 – получилось десяток.
Записываем в разряде десятков число 3.
Читаем ответ: 32.
2) 32 : 32 = 1
Если число разделить на само себя. то получится 1.
3) 100 – 1 = 99
3 1 2
90 – (48 – 18) ∙ 1 = 60
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 48 – 18 = (40 – 10) + (8 – 8) = 30 + 0 = 30
2) 30 ∙ 1 = 30
При умножении любого числа на 1 получается то число, которое умножали.
3) 90 – 30 = 60
Оформляем задание в тетрадь.
0 : 9 = 0
0 : 24 = 0
0 ∙ 33 = 0
(35 + 46) · 0 = 81 · 0 = 0
(82 – 82) : 3 = 0 : 3 = 0
(30 – 29) · 8 = 1 · 8 = 8
87 : (85 + 2) – 1 = 87 : 87 – 1 = 1 – 1 = 0
100 – 32 : (16 + 16) = 100 – 32 : 32 = 100 – 1 = 99
90 – (48 – 18) · 1 = 90 – 30 · 1 = 90 – 30 = 60
Расставляем порядок действий и выполняем вычисления.
3 1 2
60 – (16 – 9) · 4 = 32
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 16 – 9 = 16 – (6 + 3) = (16 – 6) – 3 = 10 – 3 = 7
2) 7 ∙ 4 = 28
3) 60 – 28 = 32
-(2023).jpg)
2 1 3
56 : (13 – 5) + 9 = 16
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – деление, а потом сложение.
1) 13 – 5 = 13 – (3 + 2) = (13 – 3) – 2 = 10 – 2 = 8
2) 56 : 8 = 7,так как 8 · 7 = 56
3) 7 + 9 = 7 + (3 + 6) = (7 + 3) + 6 = 10 + 6 = 16
2 1
42 + 72 : 9 = 50
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом действие сложение.
1) 72 : 9 = 8, так как 9 · 8 = 72
2) 42 + 8 = 40 + (2 + 8) = 40 + 10 = 50
2 1
60 – 54 : 6 = 51
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом действие вычитание.
1) 54 : 6 = 9, так как 6 · 9 = 54
2) 60 − 9 = (50 + 10) – 9 = 50 + (10 – 9) = 50 + 1 = 51
3 2 1
93 − 7 · (15 − 8) = 44
В данном выражении присутствуют действия вычитания и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действия в не скобок – умножение, а потом вычитание.
1) 15 - 8 = 15 – (5 + 3) = (15 – 5) – 3 = 10 – 3 = 7
2) 7 ∙ 7 = 49
3) 93 - 49 = 93 – (43 + 6) = (93 – 43) – 6 = 50 – 6 = 44
1 3 2
8 ∙ 9 + 64 : 8 = 80
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие– умножение и деление по порядку слева направо, а потом действие – сложение.
1) 8 ∙ 9 = 72
2) 64 : 8 = 8, так как 8 · 8 = 64
3) 72 + 8 = 70 + (2 + 8) = 70 + 10 = 80
Оформляем задание в тетрадь.
60 – (16 – 9) · 4 = 60 – 7 · 4 = 60 – 28 = 32
56 : (13 – 5) + 9 = 56 : 8 + 9 = 7 + 9 = 16
42 + 72 : 9 = 42 + 8 = 50
60 – 54 : 6 = 60 – 9 = 51
93 – 7 · (15 – 8 ) = 93 – 7 · 7 = 93 – 49 = 54
8 · 9 + 64 : 8 = 72 + 8 = 80
Номер 7.
Используя знаки умножения и деления, составь верные равенства с числами:
18, 24, 3, 8, 27, 9, 6, 2.
Ответ:
2 ∙ 3 = 6 6 ∙ 3 = 18 9 ∙ 2 = 18
6 : 3 = 2 18 : 6 = 3 18 : 2 = 9
6 : 2 = 3 18 : 3 = 6 18 : 9 = 2
3 ∙ 8 = 24 9 ∙ 3 = 27
24 : 8 = 3 27 : 9 = 3
24 : 3 = 8 27 : 3 = 9
Помни, что равенство – числовое выражение, составленное из чисел, знаков арифметических действий, скобок и знака равно.
Составим выражения со знаком умножение.
3 ∙ 2 = 6
2 ∙ 9 = 18
3 ∙ 8 = 24
3 ∙ 3 = 9
3∙ 9 = 27
3 ∙ 6 = 18
6 ∙ 3 = 18
Составим выражения со знаком деление.
6 : 2 = 3
6 : 3 = 2
18 : 9 = 2
18 : 2 = 9
24 : 3 = 8
24 : 8 = 3
9 : 3 = 3
27 : 3 = 9
27 : 9 = 3
18 : 3 = 6
18 : 6 = 3
Номер 8.
Реши уравнения с устным объяснением.
x · 12 = 12 x : 9 = 0 25 : x = 25 x : 9 = 1
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия вычитания и сложения.
Рассуждение.
х · 12 = 12
х – неизвестный множитель.
Чтобы найти неизвестный множитель нужно значение произведения разделить на известный множитель.
х : 9 = 0
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делитель.
25 : х = 25
х – неизвестный делитель.
Чтобы найти делитель, нужно делимое разделить на частное.
х : 9 = 1
х – неизвестное делимое.
Чтобы найти делимое, нужно частное умножить на делитель.
Промежуточные вычисления и объяснения.
x ∙ 12 = 12
x = 12 : 12
x = 1
Значение произведения равно одному из множителей, это может быть в том случае если второй множитель равен 1.
x : 9 = 0
x = 9 ∙ 0
x = 0
Делитель равен 9, а значение частного равно 0, это может быть в том случае если делимое тоже равно 0.
25 : x = 25
x = 25 : 25
x = 1
Делимо и значение частного равны, это может быть в том случае если делили на 1.
x : 9 = 1
x = 1 ∙ 9
x = 9
Делитель равен 9, а значение частного равно1, это может быть в том случае если делимое и делитель равны.
Задание внизу страницы.
0 : 6 = : 9 = 0 0 : 100 =
Ответ:0 : 6 = 0 0 : 9 = 0 0 : 100 = 0
Чтобы понять, какие числа вписать в окошки проанализируй записи и подумай, при каких значениях чисел в квадратиках данные записи обращаются в верные равенства.
Рассуждение.
0 : 6 =
Делимое равно 0, а делитель – 6. При делении нуля на любое число , не равное 0, получается 0.
Записываем вместо окошка 0.
: 9 = 0
Делитель равен 9, а значение частного – 0. Делимое неизвестно, но из-за того, что значение частного равно 0, то вместо окошка ставим число 0, так как если 0 разделить на любое число, не равное 0, то получается 0.
0 : 100 =
Делимое равно 0, а делитель – 100. Чтобы понять, чему равно значение частного, нужно вспомнить, что при делении нуля на любое число, не равное нулю, получается нуль.
Записываем вместо окошка 0.
Оформляем задание в тетрадь.
0 : 6 = 0
0 : 9 = 0
0 : 100 = 0
Если 0 разделить на любое число, не равное нулю, то значение частного равно 0.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.