Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 82

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Умножение на 1
Номер 1.
Ответ:
7 ∙ 1 = 7
1 ∙ 12 = 12
83 ∙ 1 = 83
1 ∙ 27 = 27

1) При умножении любого числа на 1, получается число, которое умножали.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним умножение.
7 · 1 = 7,
где 7 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
При умножении любого числа на 1 получается то число, которое умножали.
1 · 12 = 12 · 1 = 12,
где 12 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При умножении любого числа на 1получается то число, которое умножали.
Расставляем порядок действий и выполняем вычисления.
2 1
52 ∙ (48 − 47) = 52
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок умножение.
1) 48 – 47 = 1
2) 52 ∙ 1 = 52
1 2
(62 + 24) ∙ 1 = 86
В данном выражении присутствуют действия сложение и умножение, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок умножение.
1) 62 + 24 = 86
2) 86 ∙ 1 = 86
Выполним умножение.
83 · 1 = 83,
где 83 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
При умножении любого числа на 1получается то число, которое умножали.
1 · 27 = 27 · 1 = 27,
где 27 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При умножении любого числа на 1получается то число, которое умножали.
Выполним вычисления по действиям.
1 2
28 : 4 · 1 = 7
В данном выражении присутствуют действия умножение и деление – они равносильны. выполняем действия по порядку слева направо.
1) 28 : 4 = 7
2) 7 ∙ 1 = 7
1 2
1 ∙ 8 ∙ 3 = 24
В данном выражении присутствуют действия умножение и деление – они равносильны. выполняем действия по порядку слева направо.
1)1 ∙ 8 = 8
2) 8 ∙ 3 = 24
Оформляем задание в тетрадь.
7 ∙ 1 = 7
1 ∙ 12 = 12
52 · (48 – 47) = 52 · 1 = 52
(62 + 41) · 1 = 103 · 1 = 103
83 · 1 = 83
1 · 27 = 27 · 1
28 : 4 · 1 = 7 · 1 = 7
1 · 8 · 3 = 1 · 24 = 24 · 1 = 24
Номер 2.
Ответ:56 : 8 = 7 54 : 9 = 6

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним деление.
56 : 8 = 7, так как 8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
54 : 9 = 6, так как 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Расставляем порядок действий и выполняем вычисления.
1 2
81 : 9 ∙ 8 = 72
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 81 : 9 = 9
2) 9 ∙ 8 = 72
1 2
45 : 5 ∙ 7 = 63
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1) 45 : 5 = 9
2) 9 ∙ 7 = 63
1 3 2
4 ∙ 9 − 40 : 5 = 28
В данном выражении присутствуют действия вычитание, умножение и деление. Вначале выполняем действие умножение, потом – деление и последним действием выполняем вычитание.
1) 4 ∙ 9 = 36
2) 40 : 5 = 8
3) 36 − 8 = 28
1 3 2
42 : 6 + 8 ∙ 8 = 71
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие деление, потом – умножение и последним действием выполняем сложение.
1) 42 : 6 = 7
2) 8 ∙ 8 = 64
3) 7 + 64 = 71
2 1
27 : (20 − 11) = 3
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие внес скобок – деление.
1) 20 – 11 = 9
2) 27 : 9 = 3
2 1
49 : (60 – 53) = 7
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие внес скобок – деление.
1) 60 – 53 = 7
2) 49 : 7 = 7
Оформляем задание в тетрадь.
56 : 8 = 7
54 : 9 = 6
81 : 9 · 8 = 9 · 8 = 72
45 : 5 · 7 = 9 · 7 = 63
4 · 9 – 40 : 5 = 36 – 8 = 28
42 : 6 + 8 · 8 = 7 + 64 = 71
27 : (20 – 11) = 27 : 9 = 3
49 : (60 – 53) = 49 : 7 = 7
Номер 3.
В столовую привезли 36 кг яблок, а груш в 4 раза меньше. На сколько килограммов меньше привезли груш, чем яблок?
Ответ:
1-й способ решения: 1) 36 : 4 = 9 (кг) – привезли груш. 2) 36 − 9 = 27 (кг) - меньше привезли груш Ответ: на 27 кг груш меньше привезли, чем яблок.
2-й способ решения: 36 – 36 : 4 = 36 – 9 = 27 (кг) - на сколько меньше Ответ: на 27 кг.
1) «в 4 раза меньше», значит, вычисляется делением.
2) Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
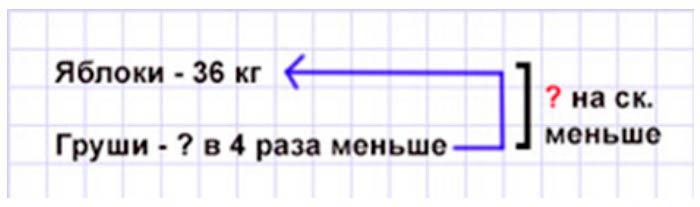
Рассуждаем.
В столовую привезли 36 кг яблок, а груш – в 4 раза меньше. Значит, чтобы узнать, сколько груш привезли в столовую, нужно количество привезенных яблок разделить на 4.
36 : 4 = 9 (кг) – привезли груш.
Продолжаем рассуждение.
Мы узнали, что привезли в столовую 36 кг яблок и 9 кг груш.
Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Значит, чтобы узнать, на сколько меньше килограмм привезли груш, чем яблок, нужно из количества яблок вычесть количество груш.
36 − 9 = 27 (кг) – на сколько меньше привезли груш, чем яблок.
Записываем ответ.
Ответ: на 27 кг груш меньше привезли, чем яблок.
Решение выражением:
36 – (36 : 4) = 27 (кг), где 36 : 4 – количество привезенных груш.
Номер 4.
18 кг варенья разложили в 6 банок поровну. Сколько надо таких банок, чтобы разложить 24 кг варенья?
Ответ:
1-й способ решения: 1) 18 : 6 = 3 (кг) – варенья в одной банке. 2) 24 : 3 = 8 (б.) - нужно для 24 кг варенья Ответ: 8 банок понадобится для 24 кг варенья.
2-й способ решения: 24 : (18 : 6) = 24 : 3 = 8 (б.) – на 24 кг варенья. Ответ: 8 банок.
Данная задача: вида «масса 1 банки, количество банок, общее количество варенья» характеризуется зависимостями между компонентами:
Масса 1 банки · количество банок = общее количество варенья.
Общее количество варенья : масса 1 банки = количество банок.
Общее количество варенья : количество банок = масса 1 банки.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество варенья складывается из количества варенья в каждой из 6 банок. Значит, чтобы узнать. Сколько варенья было в 1 банке, нужно общее количество варенья разделить на количество банок.
18 : 6 = 3 (кг) − было в каждой банке.
Продолжаем рассуждение.
Из таблицы видно, что общее количество варенья складывается из количества варенья в каждой из банок. Значит, чтобы узнать, сколько банок потребовалось для того, чтобы разлить 24 кг варенья, нужно общее количество варенья разделить на массу варенья в 1 банке.
24 : 3 = 8 (б.) − на 24 кг варенья.
Записываем ответ.
Ответ: 8 банок понадобится для 24 кг варенья.
Решение выражением:
24 : (18 : 6) = 8 (б.), где 18 : 6 – количество варенья в 1 банке.
Номер 5.
Если известно, сколько стоит книга и что блокнот в 7 раз дешевле книги, то как узнать, сколько стоит 1 блокнот? 4 блокнота?
Ответ:1-й способ решения: Чтобы узнать, сколько стоит блокнот, нужно цену книги разделить на 7. Чтобы узнать, сколько стоит 4 блокнота, нужно получившееся число умножить на 4.
2-й способ решения: Пусть х – цена книги х : 7 – цена 1 блокнота (х : 7) ∙ 4 – цена 4 блокнотов
1) «в 7 раз дешевле», значит, вычисляется делением.
2) Помни о зависимости между компонентами и результатом действия умножения.
Оформляем условие в виде таблицы.

Рассуждаем.
Сказано, что блокнот в 7 раз дешевле книги, значит, чтобы узнать, сколько стоит блокнот, нужно цену книги разделить на 7.
Обозначим стоимость книги – а рублей.
(а : 7) рублей – цена 1 блокнота.
Продолжаем рассуждение.
Блокноты одинаковые, значит, что их цена равна. Если один блокнот стоит (а : 7) рублей, а их колличесвто 4, то чтобы узнать, сколько стоят 4 блокнота, нужно цену одного блокнота умножить на количесвто блокнотов.
(а : 7) · 4 – цена 4 блокнотов, где а : 7 – цена 1 блокнота.
Записываем ответ.
Ответ:
1) Чтобы узнать, сколько стоит блокнот, нужно цену книги разделить на 7.
2) Чтобы узнать, сколько стоит 4 блокнота, нужно получившееся число умножить на 4.
Номер 6.
1) Начерти 2 таких квадрата, чтобы периметр первого был равен 8 см, а периметр второго был бы в 3 раза больше.
2) Во сколько раз сторона первого квадрата меньше, чем сторона второго?
3) Во сколько раз площадь второго квадрата больше площади первого?
1.

2. 1) 8 : 4 = 2 (см) – сторона 1 квадрата.
2) 8 ∙ 3 = 24 (см) – периметр 2 квадрата.
3) 24 : 4 = 6 (см) – сторона 2 квадрата.
4) 6 : 2 = 3 (раз)
Ответ: в 3 раза меньше сторона первого квадрата меньше, чем второго.
3. 1) 2 ∙ 2 = 4 (см2) – площадь 1 квадрата.
2) 6 ∙ 6 = 36 (см2) – площадь 2 квадрата.
3) 36 : 4 = 9 (раз)
Ответ: в 9 раз больше площадь второго квадрата, чем первого.
1) «в 3 раза больше», значит, вычисляется умножением.
2) Чтобы вычислить площадь фигуры, нужно длину умножить на ширину.
Оформляем условие в виде таблицы.

Рассуждаем.
Периметр квадрата – это сумма длин всех сторон. Значит, чтобы вычислить периметр квадрата, нужно сложить длины сторон квадрата.
Но стороны квадрата равны, значит, сложение одинаковых слагаемых можно заменить умножением. Поэтому чтобы найти сторону квадрата нужно периметр разделить на количество сторон.
8 : 4 = 2 (см) – длина стороны певрого квадрата
Продолжаем рассуждение.
Мы знаем, что периметр второго квадрата в 3 раза больше, чем периметр первого квадрата. Это значит, что величину периметра первого квадрата нужно сложить 3 раза. Но сложение одинаковых слагаемых можно заменить умножением.
8 · 3 = 24 (см) – периметр второго квадрата.
Продолжаем рассуждение.
Чтобы вычислить периметр второго квадрата, нужно сложить длины сторон квадрата.
Но стороны квадрата равны, значит, сложение одинаковых слагаемых можно заменить умножением. Поэтому чтобы найти сторону квадрата нужно периметр разделить на количество сторон.
24 : 4 = 6 (см) – длина стороны второго квадрата.
Начертим квадраты.
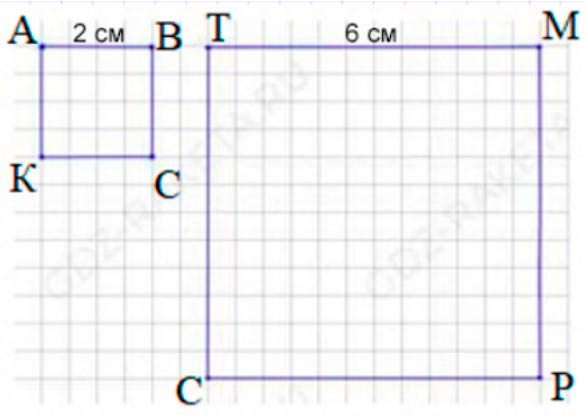
Рассуждаем.
Мы узнали, что периметр первого квадрата – 8 см, а второго – 24 см. Значит, вычислим, чему равна сторона каждого квадрата, помня, что периметр – сумма длин всех его сторон.
Значит, чтобы найти длину стороны квадрата нужно периметр квадрата разделить на 4.
8 : 4 = 2 (см) – сторона первого квадрата.
24 : 4 = 6 (см) – сторона второго квадрата.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз сторона первого квадрата меньше, чем сторона второго квадрата, нужно длину большей стороны разделить на длину стороны меньшего квадрата.
6 : 2 = 3 (р.) – во сколько раз сторона первого квадрата меньше стороны второго квадрата
Записываем ответ.
Ответ: в 3 раза меньше.
Оформляем условие в виде таблицы.

Расссуждаем.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
2 · 2 = 4 (см2) – площадь первого квадрата.
6 · 6 = 36 (см2) – площадь второго квадрата.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз площадь пощадь второго квадрата больше площади первого квадрата, нужноплощадь большего квадрата разделить на площадь меньшего квадрата.
36 : 4 = 9 (раз) – во сколько раз больше.
Значит площадь второго квадрата больше площади первого квадрата в 8 раз.
Записываем ответ.
Ответ: больше в 9 раз.
Номер 7.
Ответ:
Помни о названии компонентов действия деления и о том, какие зависимости существуют между компонентами и результатами действия деления.
Рассуждение.
х : 8 = 3,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
24 : х = 4,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
3 : 3 = х,
х – неизвестное значение частного.
Чтобы найти неизвестное значение частного, нужно делимое разделить на делитель.
49 : х = 7,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
14 : 7 = х,
х – неизвестное значение частного.
Чтобы найти неизвестное значение частного, нужно делимое разделить на делитель.
35 : х = 5,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
Промежуточные вычисления.
х : 8 = 3
х = 8 · 3
х = 24
24 : х = 4
х = 24 : 4
х = 6
3 : 3 = х
х = 3 : 3
х = 1
49 : х = 7
х = 49 : 7
х = 7
14 : 7 = х
х = 14 : 7
х = 2
35 : х = 5
х = 35 : 5
х = 7
Заполним таблицу.
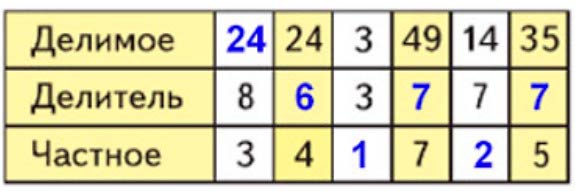
Задание внизу страницы
Ответ:89 ∙ 1 = 89 0 ∙ 99 = 0

1) Помни при умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
3) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
4) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
5) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним умножение.
89 · 1 = 89,
где 89 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
При умножении любого числа на 1, получается число, которое умножали.
Расставляем порядок действий и выполняем вычисления.
1 2
(70 − 69) · 14 = 1
В данном выражении присутствуют действия вычитание и умножение, а также скобки вначале выполним действие в скобках – вычитание, а потом действие внес скобок – умножение.
1) 70 – 69 = 1
2) 1 ∙ 14 = 14
Выполним умножение.
0 · 99 = 0,
При умножении любого числа на нуль получается нуль.
Расставляем порядок действий и выполняем вычисления.
2 1
32 − (0 · 57) = 32
В данном выражении присутствуют действия вычитание и умножение, а также скобки вначале выполним действие в скобках – умножение, а потом действие внес скобок – вычитание.
1) 0 ∙ 57 = 0
2) 32 − 0 = 32
Оформляем задание в тетрадь.
89 ∙ 1 = 89
(70 – 69) · 14 = 1 · 14 = 14 · 1 = 14
0 · 99 = 0
32 – (0 · 57) = 32 – 0 = 32
Задание на полях страницы
Набери 40:

40 = 14 + 10 + 16 40 = 28 + 2 + 10 40 = 20 + 18 + 2 40 = 13 + 10 + 17
Подбери такие комбинации чисел, чтобы при сложении получалось 40. Для этого складывай разные числа, чтобы найти верное решение, которых существует множество.
Устные рассуждения.
Складывая данные числа нужно набрать число 40.
Оформляем задание в тетрадь.
28 + 2 + 10 = 40
14 + 16 + 10 = 40
17 + 13 + 10 = 40
18 + 2 + 20 = 40
Задание в начале страницы.
Вспомни, как деление связано с умножением. Вычисли с устным объяснением.
1 · 13 = 13 13 : 13 = 13 : 1 = 1 · 27 = 27 : 27 = 27 : 1 =
1 · a = a
a : 1 = a
a : a = 1, при этом a не равно 0.
1 · 27 = 27 13 : 13 = 1 27 : 27 = 1 13 : 1 = 13 27 : 1 = 27
Вспомни о зависимости между компонентами и результатами действий деления, умножении.
Рассуждаем.
1 · 13 = 13, так как если 1 умножить на любое число, то получим 13.
13 : 13 = 1, так как если значение произведения разделить на известный множитель, то получим неизвестный множитель.
13 : 1 = 13, так как если значение произведения разделить на известный множитель, то получим известный множитель.
1 · 27 = 27, так как если 1 умножить на любое число, то получим 27.
27 : 27 = 1, так как если значение произведения разделить на известный множитель, то получим неизвестный множитель.
27 : 1 = 27, так как если значение произведения разделить на известный множитель, то получим неизвестный множитель.
Оформляем задание в тетрадь.
1 ∙ 13 = 13
1 ∙ 27 = 27
Если число умножить на 1, то число не изменится.
13 : 13 = 1
27 : 27 = 1
Если число разделить на само себя, то получится 1.
13 : 1 = 13
27 : 1 = 27
Если число разделить на 1, то число не изменится.
Номер 1.
Закончи выводы и приведи свои примеры.
1) При делении числа на то же самое число, не равное 0, получается ... . 2) При делении числа на 1 получается ... .
Ответ:1) При делении числа на то же самое число. Не равное 0, получается единица. Например, 5 : 5 = 1, 6 : 6 = 1. 2) При делении числа на 1 получается это же число (уменьшаемое). Например: 10 : 1 = 10, 2 : 1 = 2, 5 : 1 = 5
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Продолжим фразу.
При делении числа на то же самое число, не равное 0, получается 1.
Приведём примеры.
9 : 9 = 1
8 : 8 = 1
7 : 7 = 1
Продолжим фразу.
При делении числа на 1 получается то же самое число.
Приведём примеры.
9 : 1 = 9
8 : 1 = 8
7 : 1 = 7
Номер 2.
За день в магазине продали 36 детских велосипедов, а взрослых велосипедов на 27 меньше. Во сколько раз меньше продали взрослых велосипедов, чем детских?
Ответ:
1) 36 – 27 = 9 (в.) – взрослых продали. 2) 36 : 9 = 4 (раз.) Ответ: в 4 раза меньше было продано взрослых велосипедов, чем детских.
1) «на 27 меньше», значит, вычисляется вычитанием.
2) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
За день в магазине продали 36 детских велосипедов, а взрослых – на 27 штук меньше. На 27 меньше, значит, что их продали столько же, сколько детских, но без 27 штук. Значит, чтобы узнать, сколько было продано взрослых велосипедов, нужно из количества детских велосипедов вычесть 27 штук.
36 − 27 = 9 (в.) – взрослые.
Продолжаем рассуждение.
Детских велосипедов в магазине было 36, а взрослых – 9.
Чтобы узнать, во сколько раз меньше было взрослых велосипедов, чем детских, нужно количество детских велосипедов разделить на количество детских.
36 : 9 = 4 (раз.) – во сколько меньше.
Записываем ответ.
Ответ: в 4 раза меньше было продано детских велосипедов, чем взрослых.
Решение выражением: 36 : (36 – 27) = 4 (раза), где 36 – 27 – количество проданных взрослых велосипедов.
Номер 3.
Дима пошёл в театр. Через некоторое время, в 10 ч 20 мин, его старший брат Кирилл обнаружил, что младший брат забыл взять входной билет. Как поступить Кириллу: догонять Диму или нет, если спектакль начинается в 11 ч? Какие дополнительные данные нужны, чтобы Кирилл смог принять решение? Введи их, сделай вывод и подтверди его вычислениями.
Ответ:Чтобы Кирилл принял решение, надо знать следующие данные: 1) Время, в которое вышел Дима 2) Время, которое нужно потратить от дома до театра Если Дима вышел в 10.00 (любое время от 10.00 до 10.19) и от дома до театра 20 мин (от 20 мин до 30 мин), то Кирилл может успеть 10 ч 00 мин + 20 мин = 10 ч 20 мин Если до театра добираться больше 40 мин, то Кирилл не успеет принести билеты 10 ч 20 мин + 40 мин = 11 ч – начало спектакля
1 час = 60 минут.
1 минута = 60 секунд.
Рассуждаем.
Чтобы Кирилл принял решение, надо знать следующие данные:
1) Время, в которое вышел Дима.
2) Время, которое нужно потратить от дома до театра.
Продолжаем рассуждение.
Если Дима вышел в 10.00 (любое время от 10.00 до 10.19) и от дома до театра 20 мин (от 20 мин до 30 мин), то Кирилл может успеть.
10 ч 00 мин + 20 мин = 10 ч 20 мин.
Если до театра добираться больше 40 мин, то Кирилл не успеет принести билеты.
10 ч 20 мин + 40 мин = 11 ч – начало спектакля.
Номер 4.


Помни о названии компонентов действия сложения и зависимости между компонентами и результатом действия сложения.
Рассуждение.
46 + 18 = х,
х – неизвестное значение суммы.
Чтобы найти неизвестное значение суммы, нужно сложить известные слагаемые.
46 + х = 74,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х + 38 = 84,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
36 + х = 74,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х + 28 = 64,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
36 + х = 54,
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
Промежуточные вычисления.
46 + 18 = х
х = 46 + 18
х = 64
Значение суммы равно 64.
46 + х = 74
х = 74 – 46
х = 28
Неизвестное слагаемое равно 28.
х + 38 = 84
х = 84 – 38
х = 46
Неизвестное слагаемое равно 46.
36 + х = 74
х = 74 – 36
х = 38
Неизвестное слагаемое равно 38.
х + 28 = 64
х = 64 – 28
х = 36
Неизвестное слагаемое равно 36.
36 + х = 54
х = 54 – 36
х = 18
Неизвестное слагаемое равно 18.
Заполним таблицу.
.jpg)
Номер 5.
15 : 1 0 · (36 – 19) 18 : 18 (24 – 15) : 1 84 : 1 (18 + 45) : 63 71 – 45 + 0 70 : 10 56 + 26 – 0 80 : 8 0 + 93 – 13 90 : 10
Ответ:15 : 1 = 15 70 : 10 = 7 18 : 18 = 1 80 : 8 = 10 84 : 1 = 84 90 : 10 = 9

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Выполняем деление.
15 : 1 = 15, так как если любое число разделить на 1, то получится это же число.
18 : 18 = 1, так как если число разделить на само себя, то получится единица.
84 : 1 = 84, так как если любое число разделить на 1, то получится это же число.
Выполним вычисления по действиям.
2 1
0 · (36 – 19) = 0
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
1) 36 – 19 = 17
-(2023).jpg)
Вычитаем единицы. От числа 6 мы не можем отнять 9.
Занимаем 1 дес. = 10 ед., 10 + 6 = 16 ед., 16 – 9 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 2 дес.,
2 – 1 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 17.
2) 0 ∙ 17 = 0
При умножении любого числа на нуль получается нуль.
1 2
(24 – 15) : 1 = 9
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – деление.
1) 24 – 15 = 9
-(2023).jpg)
Вычитаем единицы. От числа 4 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 + 4 = 14 ед., 14 – 5 = 9 – получилось единиц.
Записываем в разряде единиц число 9.
Вычитаем десятки. Было 2 дес., мы занимали 1 дес, осталось 2 – 1 = 1 дес.,
1 – 1 = 0 – получилось десятков.
Числа в разряде десятков нет.
Читаем ответ: 9.
2) 9 : 1 = 9
При делении числа на нуль, получается тоже самое число.
1 2
(18 + 45) : 63 = 1
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом действие вне скобок – деление.
1) 18 + 45 = 63
-(2023).jpg)
Складываем единицы. 8 + 5 = 13 – получилось 1 дес. и 3 ед.
Записываем в разряде единиц число 3, а 1 дес. запоминаем.
Складываем десятки. 1 + 4 = 5 и ещё 1 дес., который запомнили 5 + 1 = 6 – получилось десяток.
Записываем в разряде десятков число 6.
Читаем ответ: 63.
2) 63 : 63 = 1
Если число разделить на само себя. то получится нуль.
1 2
71 – 45 + 0 = 26
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем действия по порядку слева направо.
1) 71 – 45 = 26
-(2023).jpg)
Вычитаем единицы. От числа 1 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 + 1 = 11 ед., 11 – 5 = 6 – получилось единиц.
Записываем в разряде единиц число 6.
Вычитаем десятки. Было 7 дес., мы занимали 1 дес, осталось 7 – 1 = 6 дес.,
6 – 4 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 26.
2) 26 + 0 = 26
Если к числу прибавить нуль, то число не изменится.
1 2
56 + 26 – 0 = 82
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем действия по порядку слева направо.
1) 56 + 26 = 82
-(2023).jpg)
Складываем единицы. 6 + 6 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. 5 + 2 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десяток.
Записываем в разряде десятков число 8.
Читаем ответ: 82.
2) 82 − 0 = 82
Если из числа вычесть нуль, то число не изменится.
1 2
0 + 93 − 13 = 80
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем действия по порядку слева направо.
1) 0 + 93 = 93
Если к числу прибавить нуль, то число не изменится.
2) 93 − 13 = (90 – 10) + (3 – 3) = 80 + 0 = 80
Выполним деление.
70 : 10 = 7, так как 10 · 7 = 70, где 10 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
80 : 8 = 10, так как 8 · 10 = 80, где 8 – одинаковое слагаемое, а 10 – количество одинаковых слагаемых.
90 : 10 = 9, так как 10 · 9 = 90, где 10 – одинаковое слагаемое, а 10 – количество одинаковых слагаемых.
Оформим задание в тетрадь.
15 : 1 = 15
18 : 18 = 1
84 : 1 = 84
0 · (36 – 19) = 0 · 17 = 0
(24 – 15) : 1 = 9 : 1 = 9
(18 + 45) : 63 = 63 : 63 = 1
71 – 45 + 0 = 71 – 45 = 26
56 + 26 – 0 = 56 + 26 = 80 + 22 = 92
0 + 93 – 13 = 93 – 13 = 80
70 : 10 = 7
80 : 8 = 10
90 : 10 = 9
Номер 6.
1) Площадь какой фигуры, 1 или 2, больше? 2) Периметр какой фигуры, 1 или 2, меньше? 3) Можно ли все части фигуры 1 назвать четырёхугольниками? А прямоугольниками?

1) Площадь фигуры 1 больше. 2) Периметр фигуры 2 меньше. 3) Да, все части фигуры 1 можно назвать четырёхугольниками (у них по 4 угла), но не все из них прямоугольники (в прямоугольнике все 4 угла прямые).
1) Площадь – часть плоскости, которую занимает фигура.
2) Чтобы вычислить площадь фигуры, нужно длину умножить на ширину.
Рассуждаем.
Площадь данных фигур вычислить по формуле нельзя, то есть применить формулу площади.
Вычислим площадь фигур в клетках.
Площадь фигуры складывается из суммы площадей всех фигур, из которых она состоит.
Значит, чтобы вычислить площадь большой фигуры, нужно вычислить площадь маленьких фигур и их сложить.
Найдём площадь 1 фигуры.
-(2023).jpg)
Желтая маленькая фигура – 2 клетки.
Синяя маленькая фигура – 8 клеток.
Зелёная маленькая фигура – 12 клеток, так как если фигуру разбить на 3 части, то получим прмяоугольник из 8 квадратов и два треугольника, в сумме которые дают 4 квадрата.
-(2023).jpg)
2 + 8 + 12 = 22 (кл.) – площадь первой фигуры.
Найдём площадь 2 фигуры.
-(2023).jpg)
Оранжевая маленькая фигура – 12 клеток, так как если фигуру разбить на 3 части, то получим прямоугольник из 8 квадратов и два треугольника, в сумме которые дают 4 квадрата.
-(2023).jpg)
Зелёная маленькая фигура – 8 клеток.
12 + 8 = 20 (кл.) – площадь второй фигуры.
Сравним площади фигур.
22 кл. > 20 кл.
Площадь первой фигуры больше, чем площадь первой фигуры на 2 клетки.
Записываем ответ.
Ответ: площаль фигуры 1 больше.
Рассуждаем.
Периметр данных фигур вычислить по формуле нельзя, то есть применить формулу периметра.
Прежде, чем вычислить периметры фигур, нужно сначала проанализировать состав каждой фигуры.
Анализируем.
Первые фигура состоит из 3 частей:
Желтая маленькая фигура – 2 клетки.
Синяя маленькая фигура – 8 клеток.
Зелёная маленькая фигура – 12 клеток.
-(2023).jpg)
Вторая фигура состоит из двух частей:
Оранжевая маленькая фигура – 12 клеток.
Зелёная маленькая фигура – 8 клеток.
-(2023).jpg)
Очевидно, что периметр второй фигуры меньше, чем первой фигуры.
Записываем ответ.
Ответ: периметр фигуры 2 меньше.
Рассуждаем.
Четырехугольник – геометрическая фигура, у которой 4 угла, 4 стороны, 4 вершины.
Прямоугольник – четырехугольник, у которого стороны попарно равны, а все углы прямые.
Первая фигура состоит из трёх частей:
Желтая маленькая фигура – прямоугольник
Синяя маленькая фигура – прямоугольник
Зелёная маленькая фигура – четырёхугольник, но не прямоугольник.
Первая фигура составлена из трех четырехугольников, значит, можно сказать, все части фигуры 1 – четырехугольники.
Но не каждая из частей – прямоугольник, так как у зелёной фигуры нет прямых углов.
Поэтому, нельзя сказать, что все части фигуры 1 – прямоугольники.
Записываем ответ.
Ответ: четырёхугольники – да, а прямоугольники – нет.
Оформляем задание в тетрадь.
Задание 1. Площадь первой фигуры больше, чем второй, на площадь желтой фигуры.
Задание 2. Периметр второй фигуры меньше.
Задание 3. Все части 1 фигуры можно назвать четырехугольниками, так как у всех них по 4 угла.
Нельзя все части 1 фигуры назвать прямоугольниками, так как у зеленой части углы не прямые.
Задание в низу страницы.
5 : 5 = 8 : = 1 : 12 = 1
Ответ:5 : 5 = 1 8 : 8 = 1 12 : 12 = 1
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Рассмотрим выражения.
Запишем все выражения в виде уравнения, где вместо окошка, подставив х:
5 : 5 = х,
х – неизвестное значение частного.
Чтобы найти неизвестное значение частного, нужно делимое разделить на делитель.
8 : х = 1,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
х : 12 = 1,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Решим уравнения.
5 : 5 = х
х = 1
Если число разделить на само себя, то получится 1.
8 : х = 1
х = 8 : 1
х = 8
Если число разделить на 1, то число не изменится.
х : 12 = 1
х = 1 · 12
х = 12
Если число умножить на 1, то число не изменится.
Оформляем задание в тетрадь.
5 : 5 = 1
8 : 8 = 1
12 : 12 = 1
Задание на полях страницы.


В этих фигурах есть прямоугольник (2 см на 1 см), трапеция. Но они различаются расположением и цветом. Кроме этого в первой фигуре есть еще маленький прямоугольник.
Сравнить рисунки, т.е. рассмотреть их с разных сторон: какого цвета фигуры, сколько их, какие.
Заполним имеющимися данными таблицу и проанализируем.
-(2023).jpg)
Применяя таблицу выпишем сходство фигур.
1. Фигуры состоят из четырехугольников.
2. Фигуры симметричны.
3. В фигурах все четырёхугольники разного цвета.
Применяя таблицу выпишем различие фигур.
1. В первой фигуре 3 части, а во второй – две.
2. Площадь первой фигуры больше, чем второй.
3. Периметр первой фигуры больше, чем второй.
Оформляем задание в виде таблицы.
-(2023).jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.