Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 72

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Составь по таблице три задачи и реши их.

Задача 1:
Мама купила 6 конфет по 4 рубля за штуку.
Сколько заплатила мама за покупку?
6 ∙ 4 = 24 (руб.)
Ответ: 24 рубля заплатила мама за покупку.
Задача 2:
Мама купила за 24 рубля несколько конфет. Одна конфета стоит 4 р.
Сколько конфет купила мама?
24 : 4 = 6 (к.)
Ответ: 6 конфет купила мама.
Задача 3:
Мама купила 6 конфет за 24 рубля. Сколько стоит одна конфета?
24 : 6 = 4 (руб.)
Ответ: 4 рубля стоит одна конфета.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Составим условие.
Мама купила 6 конфет по 4 рубля за штуку. Сколько заплатила мама за покупку?
Оформляем условие в виде таблицы.

Рассуждаем.
Мама купила 6 конфет по 4 рубля за штуку. Значит, нам известно, сколько конфет было куплено и сколько стоит одна конфета, но нам неизвестно – сколько стояли все конфеты. Общая стоимость всех конфет складывается из стоимостей всех конфет. Значит, чтобы узнать сколько стоят все конфеты, нужно сложить стоимость каждой конфеты.
Но цена конфет одинаковая, значит, за каждую конфету заплатили 4 рубля. Поэтому, сложение одинаковых слагаемых можно заменить умножением.
6 ∙ 4 = 24 (рубля) − потратила мама за 6 конфет.
Записываем ответ.
Ответ: 24 рубля заплатила мама за покупку.
Составим условие.
Мама купила за 24 рубля несколько конфет. Одна конфета стоит 4 р. Сколько конфет купила мама?
Оформляем условие в виде таблицы.

Рассуждаем.
Мама купила за 24 рубля несколько конфет, причем одна конфета стоит 4 рубля. Значит, нам известна цена конфеты и стоимость всех конфет, но неизвестно, сколько конфет купила мама. Из таблицы видно, что чтобы узнать, сколько конфет купила мама, нужно общую стоимость конфет разделить на цену конфеты.
24 : 4 = 6 (конфет) − купила мама.
Записываем ответ.
Ответ: 6 конфет купила мама.
Составим условие.
Мама купила 6 конфет за 24 рубля. Сколько стоит одна конфета?
Оформляем условие в виде таблицы.

Рассуждаем.
Мама купила 6 конфет за 24 рубля. Значит, нам известно, сколько конфет купили и сколько денег потратили, но не узнали цену одной конфеты. Из таблицы видно, что чтобы узнать. Сколько стоит одна конфета, нужно общую стоимость конфет разделить на их количество.
24 : 6 = 4 (рубля) − цена одной конфеты.
Записываем ответ.
Ответ: 4 рубля стоит одна конфета.
Номер 2.
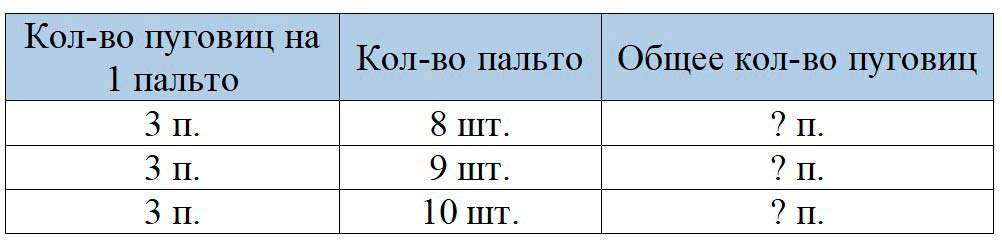
На каждое детское пальто пришивают 3 пуговицы. Сколько пуговиц нужно пришить на 8 таких пальто? на 9 пальто? на 10 пальто?
Ответ:1 пальто – 3 п. 8 пальто – ? п. 9 пальто – ? п. 10 пальто – ? п. 1) 3 ∙ 8 = 24 (п.) – на 8 пальто. 2) 3 ∙ 9 = 27 (п.) – на 9 пальто. 3) 3 ∙ 10 = 30 (п.) – на 10 пальто. Ответ: 24 пуговицы на 8 пальто, 27 пуговиц на 9 пальто, 30 пуговиц на 10 пальто.
Данная задача: вида «кол-во пуговиц на пальто, кол-во пальто, общее кол-во пуговиц» характеризуется зависимостями между компонентами:
Кол-во пуговиц на 1 пальто · кол-во пальто = общее кол-во пуговиц.
Общее кол-во пуговиц : кол-во пуговиц на 1 пальто = кол-во пальто.
Общее кол-во пуговиц : кол-во пальто = кол-во пуговиц на 1 пальто.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество пуговиц складывается из количества пуговиц на каждом пальто. Поэтому, чтобы узнать, сколько всего было пуговиц, нужно сложить количество пуговиц на каждом пальто.
Но количество пуговиц на 1 пальто одинаковое, т.е. на каждом пальто количество пуговиц равно. Значит, сложение одинаковых слагаемых можно заменить умножением.
2 ∙ 8 = 24 (п.) – нужно пришить на 8 пальто.
Записываем ответ.
Ответ: 24 пуговицы хватит на 8 пальто.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество пуговиц складывается из количества пуговиц на каждом пальто. Поэтому, чтобы узнать, сколько всего было пуговиц, нужно сложить количество пуговиц на каждом пальто.
Но количество пуговиц на 1 пальто одинаковое, т.е. на каждом пальто количество пуговиц равно. Значит, сложение одинаковых слагаемых можно заменить умножением.
3 ∙ 9 = 27 (п.) – нужно пришить на 9 пальто.
Записываем ответ.
Ответ: 27 пуговиц хватит на 9 пальто.
Оформляем условие в виде таблицы.

Рассуждаем.
Из таблицы видно, что общее количество пуговиц складывается из количества пуговиц на каждом пальто. Поэтому, чтобы узнать, сколько всего было пуговиц, нужно сложить количество пуговиц на каждом пальто.
Но количество пуговиц на 1 пальто одинаковое, т.е. на каждом пальто количество пуговиц равно. Значит, сложение одинаковых слагаемых можно заменить умножением.
3 ∙ 10 = 30 (п.) – нужно пришить на 10 пальто.
Записываем ответ.
Ответ: 30 пуговиц хватит на 10 пальто.
Оформляем условие в виде таблицы.
Записываем решение по действиям.
1) 2 ∙ 8 = 24 (п.) – на 8 пальто.
2) 3 ∙ 9 = 27 (п.) – на 9 пальто.
3) 3 ∙ 10 = 30 (п.) – на 10 пальто.
Записываем ответ.
Ответ: 24 пуговицы – на 8 пальто, 27 пуговиц – на 9 пальто, 30 пуговиц – на 10 пальто.
Номер 3.
В куске 25 м ткани. Хватит ли этой ткани, чтобы сшить 6 платьев, расходуя на каждое по 3 м ткани? Сколько метров ткани останется, если расходовать на каждое по 4 м?
Ответ:

2) 6 ∙ 4 = 24 (м)
3) 25 − 24 = 1 (м)
Ответ: да, хватит; останется 1 м, если расходовать по 4 м.
Данная задача: вида «расход ткани на 1 платье, количество платьев, общее количество ткани» характеризуется зависимостями между компонентами:
Расход ткани на 1 платье · количество платьев = общее количество ткани.
Общее количество ткани : количество платьев = расход ткани на 1 платье.
Общее количество ткани : расход ткани на 1 платье = количество платьев.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы понять, хватит ли ткани на пошив 6 пальто, расходуя на каждый по 3 метра, необходимо сначала понять, а сколько ткани потратят всего.
Нам известно количество ткани и расход ткани на 1 пальто, но неизвестно, сколько ткани израсходуют всего. При этом, общее количество ткани складывается из количества ткани, расходуемой на каждое платье. Поэтому, чтобы узнать, сколько ткани израсходовали, нужно сложить количество ткани, потраченной на каждое платье.
Но расход ткани на 1 платье одинаковое, значит, сложение одинаковых слагаемых можно заменить умножением.
6 ∙ 3 = 18 (м) − ткани нужно, чтобы сшить 6 платьев по 3 м.
Продолжаем рассуждение.
Получается, что 18 метров ткани потратили на пошив 6 одинаковых платьев. Значит, сравниваю, сколько ткани было и сколько потратили, чтобы понять, хватит ли ее.
25 м. > 18 м., значит, ткани на пошив 6 платьев хватит.
Записываем ответ.
Ответ: 25 м ткани хватит на пошив 6 платьев.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы понять, сколько ткани останется после пошива платьев, нужно сначала понять, сколько ткани израсходовали на пошив 4 платьев.
Нам известен расход на 1 платье и количество платьев, но неизвестно, сколько платьев израсходовали. Из модели к задаче видно, что чтобы узнать, сколько ткани израсходовали на 4 платья, нужно сложить ткани, расходуемое на каждое платье.
Но расход ткани на 1 платье одинаковый, значит, сложение одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько ткани потратили, можно расход ткани на 1 платье умножить на количество платьев. Вычисляется умножением.
6 ∙ 4 = 24 (м) – ткани нужно, чтобы сшить 6 платьев по 4 м на каждое.
Продолжаем рассуждение.
Значит, израсходовали 24 метра ткани. Мы знаем, что общее количество ткани складывается из количества израсходованной ткани и оставшейся. Поэтому, чтобы узнать, сколько ткани осталось, нужно из общего количества ткани вычесть количество потраченной.
25 − 24 = 1 (м) − ткани останется, если расходовать на каждое платье по 4 м.
Записываем ответ.
Ответ: 25 м ткани хватит на пошив 6 платьев по 4 м.
Решение выражением:
25 – (4 · 6),где 4 · 6 – количество потраченной ткани на 6 платьев.
Номер 4.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий.
2 1
72 − 32 : 4 = 64
В данном выражении присутствуют действия вычитание и деление. В начале выполним действие деление, а потом вычитание.
2 1
36 − 18 : 2 = 27
В данном выражении присутствуют действия вычитание и деление. В начале выполним действие деление, а потом вычитание.
2 1
48 − 24 : 3 = 40
В данном выражении присутствуют действия вычитание и деление. В начале выполним действие деление, а потом вычитание.
2 1 3
64 − 16 : 8 + 8 = 70
В данном выражении присутствуют действия сложение, вычитание и деление. В начале выполним действие деление, потом вычитание и последним действием сложение.
3 2 1
64 − 16 : (8 + 8) = 63
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. В начале выполним действие в скобках - сложение, потом деление и последним действием вычитание.
1 2 3
(64 − 16) : 8 + 8 = 14
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. В начале выполним действие в скобках - вычитание, потом деление и последним действием сложение.
2 1
9 · (13 − 6) = 63
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
6 · (27 − 20) = 42
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
40 : (30 − 25) = 8
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – деление.
Вычислим по действиям.
2 1
72 − 32 : 4 = 64
1) 32 : 4 = 8, так как 4 · 8 = 32
2) 72 − 8 = 72 – (2 + 6) = (72 – 2) – 6 = 70 – 6 = 64
Представим число 8 в виде суммы чисел 2 и 6. В начале из числа 72 вычтем число 2, а потом вычтем число 6.
2 1
36 − 18 : 2 = 27
1) 18 : 2 = 9, так как 2 · 9 = 18
2) 36 − 9 = 36 – (6 + 3) = (36 – 6) – 3 = 30 – 3 = 27
Представим число 9 в виде суммы чисел 6 и 3. В начале из числа 36 вычтем число 6, а потом вычтем число 3.
2 1
48 − 24 : 3 = 40
1) 24 : 3 = 8, так как 3 · 8 = 24
2) 48 − 8 = 40
2 1 3
64 − 16 : 8 + 8 = 70
1) 16 : 8 = 2, так как 8 · 2 = 16
2) 64 – 2 = 62
3) 62 + 8 = 70
3 2 1
64 − 16 : (8 + 8) = 63
1) 8 + 8 = 16
2) 16 : 16 = 1, если число разделить на само себя, то получится 1.
3) 62 + 1 = 63
1 2 3
(64 − 16) : 8 + 8 = 14
1) 64 — 16 = 48
2) 48 : 8 = 6, так как 8 · 6 = 48
3) 6 + 8 = 14
2 1
9 · (13 − 6) = 63
1) 13 – 6 = 7
2) 9 ∙ 7 = 63
2 1
6 · (27 − 20) = 42
1) 27 – 20 = 7
2) 6 ∙ 7 = 42
2 1
40 : (30 − 25) = 8
1) 30 – 25 = 5
2) 40 : 5 = 8, так как 5 · 8 = 40
Оформляем задание в тетрадь.
72 – 32 : 4 = 72 – 8 = 64
36 – 18 : 2 = 36 – 9 = 27
48 – 24 : 3 = 48 – 8 = 40
64 – 16 : 8 + 8 = 64 – 2 + 8 = 62 + 8 = 70
64 – 16 ∶ (8 + 8) = 64 – 16 : 16 = 64 – 1 = 63
(64 – 16) : 8 + 8 = 48 : 8 + 8 = 6 + 8 = 14
9 · (13 – 6) = 9 · 7 = 63
6 · (27 – 20) = 6 · 7 = 42
40 : (30 – 25) = 40 : 5 = 8
Номер 5.
Ответ:4 м 9 дм = 49 дм 1 дм2 = 100 см2 3 дм 4 см = 34 см 1 м2 = 100 дм2 9 см 6 мм = 96 мм 9 м = 90 дм
Помни о соотношении числовых значений единиц длины и площади.
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм
1 м = 100 см
1 дм2 = 100 см2
1 м2 = 100 дм2
Рассмотрим выражения.
4 м 9 дм = 40 дм + 9 дм = 49 дм, так как 1 м = 10 дм.
3 дм 4 см = 30 см + 4 см = 34 см, так как 1 дм = 10 см.
9 см 6 мм = 90 мм + 6 мм = 96 мм, так как 1 см = 10 мм.
1 дм2 = 10 см · 10 см = 100 см2, так как 1 дм = 10 см.
1 м2 = 10 дм · 10 дм = 100 дм2, так как 1 м = 10 дм.
9 м = 9 · 10 дм = 90 дм, так как 1 м = 10 дм
Оформляем задание в тетрадь.
4 м 9 дм = 4 ∙ 10 дм + 9 дм = 49 дм
3 дм 4 см = 3 ∙ 10 см + 4 см = 34 см
9 см 6 мм = 9 ∙ 10 мм + 6 мм = 96 мм
1 дм2 = 10 см ∙ 10 см = 100 см2
1 м2 = 10 дм ∙ 10 дм = 100 дм2
9 м = 9 ∙ 10 дм = 90 дм
Номер 6.
У входа в парк были две клумбы. Одна клумба имела форму квадрата, длина стороны которого 3 м, а другая – форму прямоугольника, длины сторон которого 4 м и 2 м. У какой клумбы площадь больше? Что можно сказать про их периметры?
Ответ:
Площадь первой клумбы больше.
Периметры одинаковые.
У какой клумбы площадь больше?
1) 3 ∙ 3 = 9 (м2) – площадь первой клумбы.
2) 4 ∙ 2 = 8 (м2) – площадь второй клумбы.
Ответ: Площадь первой клумбы больше.
Что можно сказать про их периметры?
1) 3 ∙ 4 = 12 (м) – периметр первой клумбы.
2) 4 ∙ 2 + 2 ∙ 2 = 12 (м) – периметр второй клумбы.
Ответ: Периметры одинаковые.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Чтобы вычислить площадь квадрата, нужно длину стороны умножить на сторону.
3) Периметр фигуры – суммы длин всех ее сторон.
Оформляем условие в виде краткой записи.
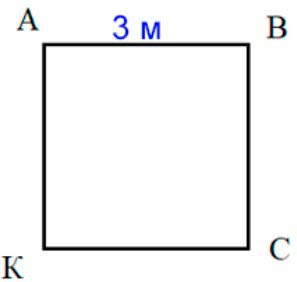
АВКС – квадрат
Длина – 3 м
Ширина – 3 м
Площадь – ?
Периметр – ?
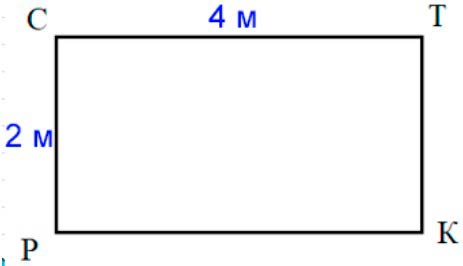
СТКР – прямоугольник
Длина – 2 м
Ширина – 4 м
Площадь – ?
Периметр – ?
Рассуждаю.
Чтобы вычислить площадь прямоугольника, нужнонайти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
3 м · 3 м = 9 (м2) – площадь квадрата.
4 м · 2 м = 8 (м2) – площадь прямоугольника.
Сравним площади:
9 м2 > 8 м2 – площадь первой клумбы больше, площади второй клумбы.
Найдём периметр квадрата.
Квадрат – замкнутая ломаная. Длина ломаной равна сумме длин всех отрезков-звеньев, значит, длина квадрата – сумма длин всех его сторон.
Получается, чтобы узнать, каков периметр квадрата, нужно сложить длины всех его сторон.
Но у квадрата все стороны равны. Значит, сложение одинаковых слагаемых можно заменить умножением. поэтому, чтобы вычислить периметр квадрата, нужно длину стороны квадрата умножить на их количество.
3 м · 4 = 12 (м) – периметр квадрата.
Найдём периметр прямоугольника.
Способ 1: сложить все стороны.
4 + 4 + 2 + 2 = (4 + 2) + (4 + 2) = 6 + 6 = 12 (м)
Споосб 2: поотдельности длину и ширину умножить на 2, а потом полученные произвдения сложить.
4 · 2 + 2 · 2 = 8 + 4 = 12 (м)
Споосб 3: сложить длину и ширину и полученную сумму умножить на 2.
(4 + 2) · 2 = 6 · 2 = 12 (м)
Сравним периметры:
12 м = 12 м – периметры клумб одинаковые.
Оформляем задание в тетрадь.
1) 3 ∙ 3 = 9 (м2) − площадь квадратной клумбы.
2) 4 ∙ 2 = 8 (м2) − площадь прямоугольной клумбы.
3) 9 > 8 − значит, площадь квадратной клумбы больше.
4) 3 ∙ 4 = 12 (м) − периметр квадратной клумбы.
5) (4 + 2) ∙ 2 = 12 (м) − периметр прямоугольной клумбы.
6) 12 = 12 − значит, площади клумб равны.
Ответ: площадь квадратной клумбы больше; периметры клумб равны.
Номер 7.
Расставь скобки так, чтобы равенства были верными.
Ответ:
1) Перебирай все возможные варианты, пока не найдешь, верное решение.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставим скобки и порядок действий.
1 2
(16 + 20) : 4 = 9
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполним действие в скобках – сложение, а потом действие вне скобок – деление.
2 1
9 ∙ (10 − 7) = 27
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
3 2 1
15 + 36 : (9 − 3) = 21
В данном выражении присутствуют действия слоение, вычитание и деление, а также скобки. В начале выполним действие в скобках – вычитание, потом действие деление и последним действием - сложение.
Вычисли по действиям.
1 2
(16 + 20) : 4 = 9
1) 16 + 20 = 30
2) 36 : 4 = 9, так как 4 · 9 = 36
2 1
9 ∙ (10 − 7) = 27
1) 10 – 7 = 3
2) 9 ∙ 3 = 27
3 2 1
15 + 36 : (9 − 3) = 21
1) 9 – 3 = 6
2) 36 : 6 = 6, так как 6 · 6 = 36
3) 15 + 6 = 21
Оформим задание в тетрадь.
(16 + 20) : 4 = 36 : 4 = 9
9 · (10 – 7) = 9 · 3 = 27
15 + 36 : (9 – 3) = 15 + 36 : 6 = 15 + 6 = 21
Задание внизу страницы
В овощную палатку привезли 8 ящиков огурцов, по 10 кг в каждом. До обеденного перерыва продали 54 кг. Сколько килограммов огурцов осталось?
Ответ:
Привезли – 8 ящ. по 10 кг
Продали – 54 кг
Осталось – ? кг
1-й способ решения:
1) 10 ∙ 8 = 80 (кг) – привезли.
2) 80 − 54 = 26 (кг)
Ответ: осталось 26 кг огурцов.
2-й способ решения: 10 ∙ 8 – 54 = 26 (кг) – осталось. Ответ: 26 кг.
Данная задача: вида «вместимость 1 ящика, количество ящиков, общее количество огурцов» характеризуется зависимостями между компонентами:
Вместимость 1 ящика · количество ящика = общее количество огурцов.
Общее количество огурцов : вместимость 1 ящика = количество ящиков.
Общее количество огурцов : количество ящиков = вместимость 1 ящика.
Оформляем условие в виде краткой записи.
Привезли – 8 ящ. по 10 кг
Продали – 54 кг
Осталось – ? кг
Рассуждаем.
В палатку привезли 8 ящиков огурцов по 10 кг в каждом. Значит, нам известно сколько огурцов в одном ящике, количество ящиков, но неизвестно, сколько всего было огурцов. При этом, общее количество огурцов складывается из количества огурцов в каждом ящике. Поэтому, чтобы узнать, сколько огурцов было всего, нужно сложить количество огурцов каждого ящика.
Но количество огурцов каждого ящика одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением. получается, нужно количество огурцов одного ящика умножить на количество ящиков.
10 ∙ 8 = 80 (кг) – привезли.
Продолжаем рассуждение.
Общее количество огурцов в палатке складывается из количества огурцов, которые продали и которые остались. Значит, чтобы узнать, сколько огурцов осталось, нужно из общего количества огурцов вычесть количество проданного.
80 − 54 = 26 (кг) – осталось.
Записываем ответ.
Ответ: осталось 26 кг огурцов.
Решение выражением:
10 · 8 – 54, где 10 · 8 – количество огурцов, которые были в палатке.
Задание на полях страницы
Магические квадраты:


Проверка:
Первый магический квадрат:
18 + 16 + 26 = 34 + 26 = 60
28 + 20 + 12 = 40 + 20 = 60
14 + 24 + 22 = 38 + 22 = 60
18 + 16 + 26 = 18 + 42 + 60
28 + 20 + 12 = 40 + 20 = 60
14 + 24 + 22 = 38 + 22 = 60
18 + 20 + 22 = 40 + 20 = 60
14 + 20 + 26 = 40 + 20 = 60
Второй магический квадрат:
21 + 28 + 23 = 49 + 23 = 72
26 + 24 + 22 = 50 + 22 = 72
25 + 20 + 27 = 52 + 20 = 72
21 + 26 + 25 = 47 + 25 = 72
28 + 24 + 20 = 52 + 20 = 72
23 + 22 + 27 = 50 + 22 = 72
21 + 24 = 27 = 45 + 27 = 72
25 + 24 + 23 = 25 + 47 = 72
Магический квадрат – квадрат, в котором числа, стоящие на одной прямой по горизонтали, вертикали и диагонали в сумме образуют одинаковое число.
Найдём магическую сумму.
.jpg)
28 + 20 + 12 = 60 – магическая сумма.
Значит, в данном магическом квадрате по горизонтали, вертикали и диагонали сумма цифр должна равняться 60.
Рассмотрим третий столбец.
В столбце не достает первого числа.
□ + 12 + 22 = 60
Упростим выражение сложив числа 12 и 22.
□ + 34 = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 34 = 26 – недостающее число во третьем столбике.
.jpg)
Рассмотрим диагональ.
В диагонали не достает первого числа.
□ + 20 + 22 = 60
Упростим выражение сложив числа 20 и 22.
□ + 42 = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 42 = 18 – недостающее число по диагонали.
.jpg)
Рассмотрим первую строчку.
В строчке не достает второго числа.
18 + □ + 26 = 60
Упростим выражение сложив числа 18 и 26.
44 + □ = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 44 = 16 – недостающее число в первой строчке.
.jpg)
Рассмотрим первый столбик.
В столбике не достает третьего числа.
18 + 28 + □ = 60
Упростим выражение сложив числа 18 и 28.
46 + □ = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 46 = 14 – недостающее число в первом столбике.
.jpg)
Рассмотрим второй столбик.
В столбике не достает третьего числа.
16 + 20 + □ = 60
Упростим выражение сложив числа 16 и 20.
36 + □ = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 36 = 24 – недостающее число во втором столбике.
.jpg)
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 60.
Найдём магическую сумму.
.jpg)
21 + 24 + 27 = 72 – магическая сумма.
Значит, в данном магическом квадрате по горизонтали, вертикали и диагонали сумма цифр должна равняться 72.
Рассмотрим первую строчку.
В строчке не достает второго числа.
21 + □ + 23 = 72
Упростим выражение сложив числа 21 и 23.
44 + □ = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 44 = 28 – недостающее число в первой строчке.
.jpg)
Рассмотрим третий столбик.
В столбике не достает второго числа.
23 + □ + 27 = 72
Упростим выражение сложив числа 23 и 27.
50 + □ = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 50 = 22 – недостающее число в третьем столбике.
.jpg)
Рассмотрим вторую строчку.
В столбике не достает первого числа.
□ + 24 + 22 = 72
Упростим выражение сложив числа 24 и 22.
46 + □ = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 46 = 26 – недостающее число во второй строке.
.jpg)
Рассмотрим первый столбик.
В столбике не достает третьего числа.
21 + 26 + □ = 72
Упростим выражение сложив числа 21 и 26.
47 + □ = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 47 = 25 – недостающее число в первом столбике.
.jpg)
Рассмотрим второй столбик.
В столбике не достает третьего числа.
28 + 24 + □ = 72
Упростим выражение сложив числа 28 и 24.
52 + □ = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 52 = 20 – недостающее число во втором столбике.
.jpg)
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 72.
Делаем вывод.
Вывод: оба квадрата магические. В первом квадрате значение суммы равно 60, а во втором – 72.
Странички для любознательных
ИМЕНА РОССИЙСКИХ УЧЁНЫХ-МАТЕМАТИКОВ 19—20 СТОЛЕТИЙ
Научные открытия меняют мир вокруг нас.
Михаил Василевич Остроградский (1801–1861)
Русский математик — один из основателей Петербургской математической школы, академик. Основные научные труды в области прикладной математики. Занимался разработкой методов определения качества изделий, водоснабжением Петербурга, участвовал в комиссиях по реформе календаря и др.

Пафнутий Львович Чебышёв (1821—1894)
Один из крупнейших математиков. Был избран членом 25 разных академий мира. Научная деятельность П. Л. Чебышёва была разнообразной. Он изобрёл «переступающий механизм» (прообраз современного шагающего устройства), гребной механизм, вычислительную машину (арифмометр непрерывного действия) и многое другое.

Софья Васильевна Ковалевская (1850–1891)
Первая в мире женщина-профессор математики. Самой важной научной работой С. В. Ковалевской было решение задач о вращении твёрдого тела вокруг неподвижной точки под влиянием действующих на него сил.

С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.