Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 71

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 4.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий.
2 1
94 − 42 : 6 = 87
В данном выражении присутствуют действия деление и вычитание. Вначале выполним действие деление, а потом вычитание.
2 1
75 + 81 : 9 = 84
В данном выражении присутствуют действия деление и сложение. Вначале выполним действие деление, а потом сложение.
2 1
38 − 64 : 8 = 30
В данном выражении присутствуют действия деление и вычитание. Вначале выполним действие деление, а потом вычитание.
2 1 3
30 − 12 : 3 + 3 = 29
В данном выражении присутствуют действия сложение, вычитание и деление. Вначале выполним действие деление, потом вычитание и последним действием сложение.
3 2 1
30 − 12 : (3 + 3) = 28
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
1 2 3
(30 − 12) : 3 + 3 = 9
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – сложение.
2 1
8 · (13 − 7) = 48
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
9 · (14 − 6) = 72
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
7 · (12 − 3) = 63
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
Вычисляем по действиям.
2 1
94 − 42 : 6 = 87
1) 42 : 6 = 7, так как 6 · 7 = 42
2) 94 − 7 = 94 – (4 + 3) = (94 – 4) – 3 = 90 – 3 = 87
Число 7 представим в виде суммы чисел 4 и 3. Вначале из числа 94 вычтем число 7, а потом вычтем число 3.
2 1
75 + 81 : 9 = 84
1) 81 : 9 = 9, так как 9 · 9 = 81
2) 75 + 9 = 75 + (5 + 4) = (75 + 5) + 4 = 80 + 4 = 84
Число 9 представим в виде суммы чисел 5 и 4. Вначале к числу 75 прибавим число 5, а потом прибавим число 4.
2 1
38 − 64 : 8 = 30
1) 64 : 8 = 8, так как 8 · 8 = 64
2) 38 − 8 = 30 + (8 – 8) = 30
2 1 3
30 − 12 : 3 + 3 = 29
1) 12 : 3 = 4, так как 3 · 4 = 12
2) 30 — 4 = 26
3) 26 + 3 = 29
3 2 1
30 − 12 : (3 + 3) = 28
1) 3 + 3 = 6
2) 12 : 6 = 2, так как 6 · 2 = 12
3) 30 — 2 = 28
1 2 3
(30 − 12) : 3 + 3 = 9
1) 30 — 12 = 18
2) 18 : 3 = 6, так как 3 · 6 = 18
3) 6 + 3 = 9
2 1
8 · (13 − 7) = 48
1) 13 – 7 = 13 – (3 + 4) = (13 – 3) – 4 = 10 – 4 = 6
Число 7 представим в виде суммы чисел 3 и 4. Вначале из числа 13 вычтем число 3, а потом вычтем число 4.
2) 8 ∙ 6 = 48
2 1
9 · (14 − 6) = 72
1) 14 – 6 = 14 – (4 + 2) = (14 – 4) – 2 = 10 – 2 = 8
Число 6 представим в виде суммы чисел 4 и 2. Вначале из числа 14 вычтем число 4, а потом вычтем число 2.
2) 9 ∙ 8 = 72
2 1
7 · (12 − 3) = 63
1) 12 – 3 = 12 – (2 + 1) = (12 – 2) – 1 = 10 – 1 = 9
Представим число 3 в виде суммы чисел 2 и 1. Вначале из числа 12 вычтем число 2, а потом вычтем число 1.
2) 7 ∙ 9 = 63
Оформляем задание в тетрадь.
94 – 42 : 6 = 94 – 7 = 87
75 + 81 : 9 = 75 + 9 = 84
38 – 64 : 8 = 38 – 8 = 30
30 – 12 : 3 + 3 = 30 – 4 + 3 = 26 + 3 = 29
30 – 12 : (3 + 3) = 30 – 12 : 6 = 30 – 2 = 28
(30 – 12) : 3 + 3 = 18 : 3 + 3 = 6 + 3 = 9
8 · (13 – 7) = 8 · 6 = 48
9 ∙ (14 – 6) = 9 · 8 = 72
7 · (12 – 3) = 7 · 9 = 63
Номер 5.
1) Маме 32 года, а сыну 8 лет. Во сколько раз мама старше сына?
2) Во сколько раз мама была старше сына 5 лет тому назад?
Задача 1:
1) 32 : 8 = 4 (раза)
Ответ: мама старше сына в 4 раза.
Задача 2:
1) 32 − 5 = 27 (л.)
2) 8 − 5 = 3 (г.)
3) 27 : 3 = 9 (р.)
Ответ: в 9 раз мама была старше сына.
1) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
Оформляем условие в виде краткой записи.

Рассуждаем.
Маме 32 года, а сыну – 8 лет. Чтобы узнать, во сколько одно число больше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз мама старше сына, нужно возраст мамы разделить на возраст сына.
32 : 8 = 4 (раза) – во столько раз мама старше сына.
Записываем ответ.
Ответ: мама старше сына в 4 раза.
Оформляем условие в виде таблицы.
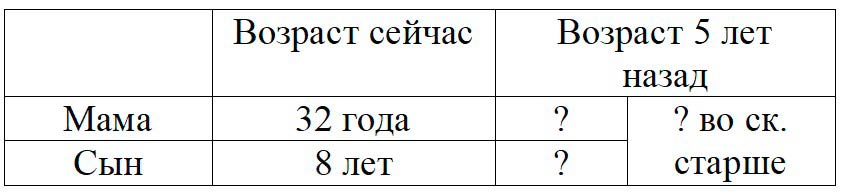
Рассуждаем.
Нужно сравнить, во сколько раз мама была старше сына 5 лет назад. Но нам неизвестно, сколько лет было маме и сыну 5 лет назад. 5 лет назад им было на 5 лет меньше, поэтому, чтобы узнать, сколько лет было маме и сыну 5 лет назад, нужно из их возраста сейчас вычесть 5 лет.
32 − 5 = 27 (лет) − было маме 5 лет тому назад;
8 − 5 = 3 (года) − было сыну 5 лет тому назад;
Продолжаем рассуждение.
Мы узнали, что 5 лет назад маме было 27 лет, а сыну – 3 года. Чтобы узнать, во сколько одно число больше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз мама старше сына, нужно возраст мамы разделить на возраст сына.
27 : 3 = 9 (раз) − во сколько раз мама была старше сына 5 лет тому назад.
Записываем ответ.
Ответ: в 9 раз мама была старше сына.
Номер 6.
По таблице на обороте обложки учебника:
1) найди произведение: 6 ∙ 7, 4 ∙ 8, 9 ∙ 3, 4 ∙ 9;
2) проверь, что 7 ∙ 8 = 8 ∙ 7, 3 ∙ 6 = 6 ∙ 3;
3) найди частное: 54 : 9, 32 : 4, 42 : 6, 35 : 5;
4) назови числа от 6 до 60, которые делятся на 6;
5) назови числа от 4 до 40, которые делятся на 4.
1) 6 ∙ 7 = 42
4 ∙ 8 = 32
9 ∙ 3 = 27
4 ∙ 9 = 36
2) 7 ∙ 8 = 8 ∙ 7 3 ∙ 6 = 6 ∙ 3
56 = 56 18 = 18
3) 54 : 9 = 6
35 : 5 = 7
32 : 4 = 8
42 : 6 = 7
4) 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
5) 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
Для выполнения задания обращайся к таблице умножения и деления чисел от 1 до 9.
Найдём произведение.
Произведение, значит, нужно найти числа, стоящие на пересечении 6 и 7, 4 и 8, 9 и 3, 4 и 9.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
9 · 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
4 · 9 = 36,
где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Проверим выражения.
Помни о существующем переместительном свойстве умножения.
Сравним 7 · 8 и 8 · 7
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
56 = 56, значит, 7 · 8 = 8 · 7
По переместительному свойству умножения.
Сравним 3 · 6 и 6 · 3.
3 · 6 = 18,
где 3 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 3 = 18,
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
18 = 18, значит, 3 · 6 = 6 · 3
По переместительному свойству умножения.
Найдём частное.
Частное – результат деления.
54 : 9 = 6,
так как 9 · 6 = 45,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
32 : 4 = 8, так как 4 · 8= 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
42 : 6 = 7, так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
35 : 5 = 7, так как 5 · 7 = 35,
где 5 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Рассуждаем.
Делятся на 6, значит, являются результатом таблицы умножения и деления 7.
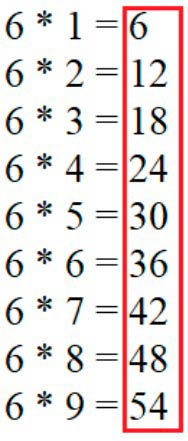
Значит, выписываю числа: 6, 12, 18, 24, 30, 36, 42, 48, 54.
Рассуждаем.
Делятся на 4, значит, являются результатом таблицы умножения и деления 9.
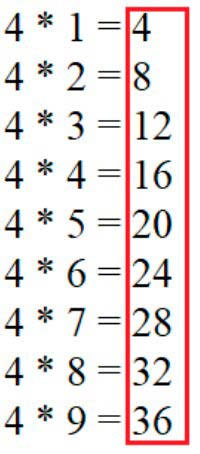
Значит, выписываю числа: 4, 8, 12, 16, 20, 24, 28, 32, 36.
Оформляем задание в тетрадь.
Задание 1.
6 ∙ 7 = 42
4 ∙ 8 = 32
9 ∙ 3 = 27
4 ∙ 9 = 36
Задание 2.
7 ∙ 8 = 8 ∙ 7
По переместительному свойству умножения.
3 ∙ 6 = 6 ∙ 3
По переместительному свойству умножения.
Здание 3.
54 : 9 = 6
32 : 4 = 8
42 : 6 = 7
35 : 5 = 7
Задание 4.
Числа от 6 до 60, которые делятся на 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
Задание 5.
Числа от 4 до 40, которые делятся на 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
Номер 7.
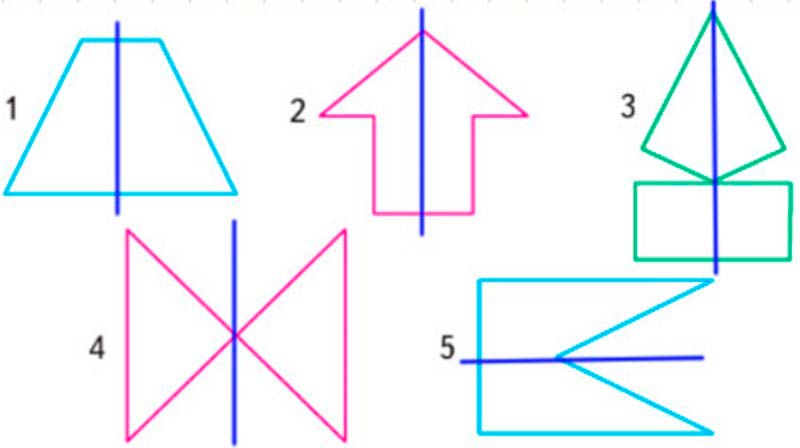
1) Начерти на листе клетчатой бумаги такой квадрат, вырежи его и разрежь по показанным на чертеже линиям.
2) Запиши номера фигур, которые ты сможешь выложить, используя полученные части квадрата.
3) Чему равна площадь каждой из этих фигур?
4) Верно ли, что все фигуры 1–5 будут симметричными?


1) Чертим квадрат, вырезаем его и разрезаем по показанным на чертеже линиям.
2) 1, 3, 5.
3) Площадь фигуры 1 равна 9 см2.
Площадь фигуры 3 равна 9 см2.
Площадь фигуры 5 равна 9 см2.
4) Да, верно, все фигуры симметричны:

1) Производи такие действия, составляй из частей фигуры, чтобы убедиться в верном решении этой задачи.
2) Чтобы вычислить площадь фигуры, нужно понять, сколько одинаковых квадратов помещается на плоскости.
3) Площадь фигуры измеряется в квадратных единицах.
Чертим и вырезаем.
Нужно начертить квадрат со стороной 3 см.
Потом полученный квадрат нужно вырезать и разрезать пополам по вертикали. А потом вторую половинку нужно полелить на два равных треугольника.
В итоге должно получиться три части: прямоугольник со сторонами 1 см 5 мм и 3 см и два треугольника.
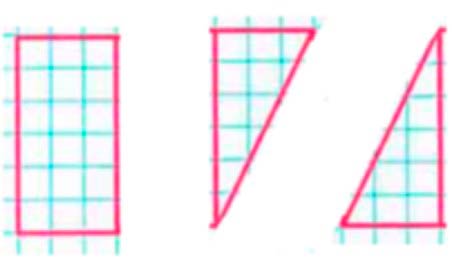
Рассуждаем.
Рассмотрим фигуру 1. Данную фигуру можно составить из полученных частей. Два треугольника постваим по бокам прямоугольника.
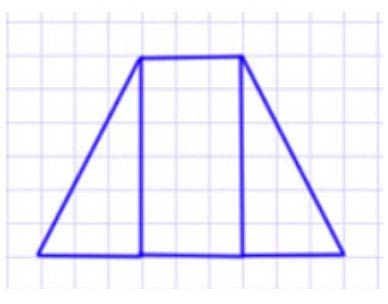
Рассмотрм фигуру 2. Из полученных частей данную фигуру составить нельзя.
Рассмотрми фигуру 3. Данную фигуру можно составить из полученных частей. Два треугольника нужно расположить над прямоугольником.
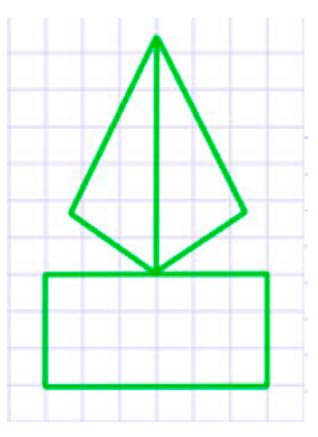
Рассмотрим фигуру 4. Из полученных частей данную фигуру составить нельзя.
Рассмотрим фигуру 5. Данную фигуру можно составить из полученных частей. Два треугольника нужно разместить с правой сторны от прямоугольника.
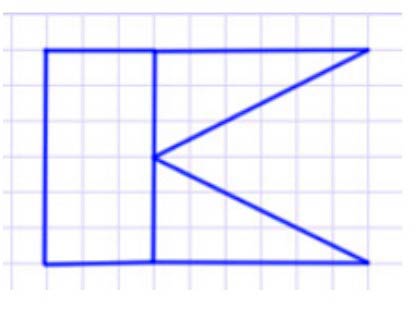
Вычисляем площади фигур.
Площадь сложной фигуры складывается из площадей фигур, из которых она составлена.
Значит, чтбы узнать, какова площадь фигур 1, 3 и 5, нужно сначала вычислить площадь фигур, которые мы вычислили. Но полученные фигуры образуют квадрат со сторной 3 см.
Так как данные фигуры состоят из одинаковых фигур: прямоугольника и двух треугольников, значит и площади этих фигур одинаковы и равны площади данного квадрата.
3 ∙ 3 = 9 (см2) – площадь фигур 1, 3, 5.
Проверим симметрию.
Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
Все фигуры имеют ось симметрии, значит они симметричны.
Задание внизу страницы
Найди по плану на с. 70 площадь огорода.

8 ∙ 3 = 24 (м2) Ответ: площадь огорода равна 24 м2.
1) Площадь фигуры измеряется в квадратных единицах.
2) Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Рассмотрим рисунок.
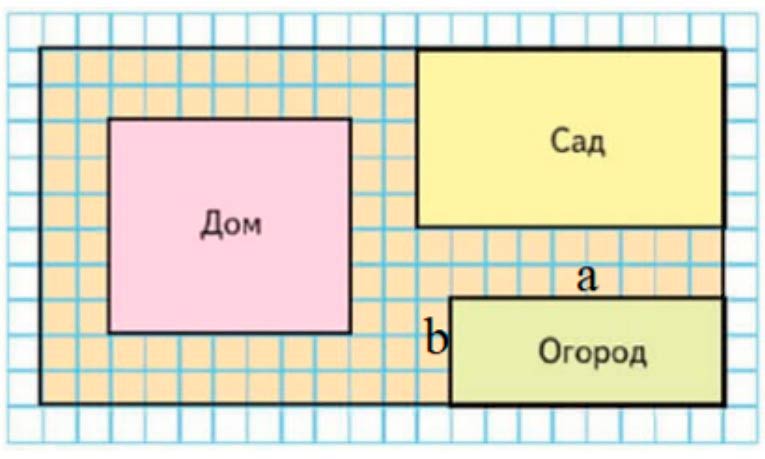
На рисунке изображён план дачного участка. Нам нужно найти площадь огорода.
Чтобы это сделать найдём длину и ширину огорода на плане и на мместности.
Длина огорода на плане равна 8 клеток, так как 1 клетка на плане равна 1 м на местности, значит:
8 · 1 м = 9 м – длина огорода на местности.
Ширина огорода на плане равна 3 клетки, так как 1 клетка на плане равна 1 м на местности, значит:
3 · 1 м = 3 м – ширина огорода на метсности.
Найдём площадь огорода.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
8 ∙ 3 = 24 (см2) – площадь огорода на местности.
Записываем ответ.
Ответ: площадь огорода 24 см2.
Номер 5.
По прямой лесной тропинке друг за другом бегут волк, лиса и заяц. Расстояние между зайцем и волком 7 м, а между зайцем и лисой 4 м. Какое расстояние может быть между лисой и волком? Кто за кем бежит? Звери могут бежать по тропинке в таком порядке: Расстояние между лисой и волком будет ▢ м. Порядок может быть и другим. Расстояние между лисой и волком будет ▢ м. В каком ещё порядке звери могли следовать друг за другом? Выполни чертёж в тетради и определи расстояние между лисой и волком для этого случая.


Расстояние между лисой и волком будет 4 + 7 = 11 м. Расстояние между лисой и волком будет 7 + 4 = 11 м. Волк — лиса — заяц. Расстояние между волком и лисой 7 – 4 = 3 м.
1) Перечислим еще раз все условия:
Расстояние между зайцем и волком – 7 метров.
Расстояние между зайцем и лисой – 4 метра.
2)Порядок следования животных важен, для определения расстоянии между ними.
Оформляем условие в виде рисунка.
-(2023).jpg)
Рассуждаем.
Звери могут бежать по тропинке в таком порядке: Лиса – заяц – волк.
Рассмотяние между лисой и волком складывается из расстояний между лисой и зайцем и расстоянием между зайцем и волком.
Значит, чтобы узнать, какое расстояние между лисой и волком, нужно сложить расстояние между лисой и зайцем с расстоянием между зайцем и волком.
4 + 7 = 11 (м) – расстояние между лисой и волком.
Записываем ответ.
Ответ: расстояние между лисой и волком 11 метров.
Оформяляем условие в в иде рисунка.
-(2023).jpg)
Рассуждаем.
Звери могут бежать по тропинке в таком порядке: Волк – заяц – лиса.
Расстояние между лисой и волком складывается из расстояний между волком и зайцем и расстоянием между айцем и лисой.
Значит, чтобы узнать, какое расстояние между лисой и волком, нужно сложить расстояние между лисой и зайцем с расстоянием между зайцем и волком.
7 + 4 = 11 (м) – расстояние между лисой и волком.
Записываем ответ.
Ответ: расстояние между лисой и волком 11 метров.
Оформляем условие в виде рисунка.
-(2023).jpg)
Рассуждаем.
Звери могут бежать по тропинке в таком порядке: Волк – лиса – заяц.
Расстояние между лисой и волком складывается из разницы между расстоянием волком и зайцем и расстоянием зайца и лисы.
Значит, чтобы узнать, какое расстояние между волком и лисой, нужноиз расстояния между волком и зайцем вычесть расстояние между лисой и зайцем.
7 – 4 = 3 (м) – расстояние между лисой и волком.
Записваем ответ.
Ответ: расстояние между лисой и волком 3 метра.
Номер 6.
Рассмотри рисунок.

Выбери высказывания, верные для данного рисунка. 1) Если фигура зелёного цвета, то это треугольник. 2) Все фигуры красного цвета — прямоугольники. 3) Все фигуры не красного цвета — треугольники. Составь ещё одно высказывание, верное для данного рисунка.
Ответ:Верные: 2, 3. Синяя фигура — не прямоугольник
1) Доказывай все высказывания или опровергай их, подбирая обоснования или опровержения.
2) Помни, что фигуру называют по количество углов. Опиши сначала все, а потом узнаешь, какие высказывания верны, а какие – нет.
Рассмотрим и опишем фигуры.
Опишем все фигуры по из свойствам: количесвто углов, цвет, размер.
Фигура 1 – большой красный прямоугольник;
Фигура 2 – маленький голубой треугольник;
Фигура 3 – большой зелёный трекгольник;
Фигура 4 – большой красный четырёхугольник (квадрат).
Рассмотрим высказывания.
1) Если фигура зеленого цвета, то это треугольник – верно, так какна рисунке только она фигура зелёного цвета и это треугольник.
2) Все фигуры красного цвета − прямоугольники – верно, так как на рисунке два красных прямоугольника – под номерами 1 и 4, но фигура 4 – это квадрат, а квадрат – это прямоугольник, у которгоьо все стороны равны.
3) Все фигуры не красного цвета − треугольники – верно, так как на рисунке красных фигур две и это четырёхугольники. А треугольник цветом – голубой и зелёный.
4) Фигура красного цвета состоит из четырех сторон – верно, так как синяя фигура только олна и это четырёхугольник.
Своё высказывание:
Синяя фигура – не прямоугольник, верно, так как на рисунке только одна синяя фигура и это треугольник.
Записываем ответ.
Ответ: все высказывания верны.
Своё высказывание: синяя фигура – не прямоугольник.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.