Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 68

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Запиши только ответы и проверь себя по таблице на обороте обложки учебника.

2 ∙ 2 = 4
3 ∙ 2 = 6
4 ∙ 2 = 8
5 ∙ 2 = 10
6 ∙ 2 = 12
7 ∙ 2 = 14
8 ∙ 2 = 16
9 ∙ 2 = 18
3 ∙ 3 = 9
4 ∙ 3 = 12
5 ∙ 3 = 15
6 ∙ 3 = 18
7 ∙ 3 = 21
8 ∙ 3 = 24
9 ∙ 3 = 27
4 ∙ 4 = 16
5 ∙ 4 = 20
6 ∙ 4 = 24
7 ∙ 4 = 28
8 ∙ 4 = 32
9 ∙ 4 = 36
5 ∙ 5 = 25
6 ∙ 5 = 30
7 ∙ 5 = 35
8 ∙ 5 = 40
9 ∙ 5 = 45
6 ∙ 6 = 36
7 ∙ 6 = 42
8 ∙ 6 = 48
9 ∙ 6 = 54
7 ∙ 7 = 49
8 ∙ 7 = 56
9 ∙ 7 = 63
8 ∙ 8 = 64
9 ∙ 8 = 72
9 ∙ 9 = 81
Вспомни таблицу умножения, обрати внимание, что записывать нужно только ответы.
Записываем ответы.

Проверяем.
Открой таблицу умножения и проверь свои ответы.
Номер 2.
В 9 одинаковых наборах 54 чашки. Сколько чашек в 5 таких наборах? Сколько таких наборов получится из 60 чашек?
Ответ:
1) 54 : 9 = 6 (ч.) – в одном наборе. 2) 5 ∙ 6 = 30 (ч.) – в пяти наборах. 3) 60 : 6 = 10 (н.) Ответ: В 5 наборах 30 чашек; в 10 наборах 60 чашек.
Данная задача: вида «кол-во чашек в 1 наборе, кол-во наборов, общее кол-во чашей» характеризуется зависимостями между компонентами:
Кол-во чашей в 1 наборе · кол-во наборов = общее кол-во чашек.
Общее кол-во чашек : кол-во наборов = кол-во чашек в 1 наборе.
Общее кол-во чашек : кол-во чашек в 1 наборе = кол-во наборов.
Оформляем условие в виде таблицы.

Рассуждаем.
В 9 одинаковых наборах 54 чашки. Значит, нам известно количество наборов и общее количество чашек, но неизвестно, сколько чашек в 1 наборе. При этом, все наборы одинаковые, т.е. количество чашек в них равно. При этом, из таблицы видно, что чтобы узнать, сколько чашек было в 1 наборе, нужно общее количество чашек разделить на количество наборов.
54 : 9 = 6 (чаш.) – в одном наборе.
Продолжаем рассуждение.
Мы узнали, что в 1 наборе – 6 чашек. Теперь необходимо узнать, сколько чашек в 5 таких наборов. Таким образом, мы знаем, сколько чашек в 1 наборе и сколько наборов, а общее количество чашек – неизвестно. Но оно складывается из количества чашек каждого набора. Поэтому, чтобы узнать, сколько чашек во всех наборах, нужно их количество сложить.
Но количество чашек в 1 наборе одинаковое, поэтому, сложение одинаковых слагаемых можно заменить умножением.
5 ∙ 6 = 30 (чаш.) – в пяти наборах.
Записываем ответ.
Ответ: в 5 наборах 30 чашек.
Решение выражением:
54 : 9 · 6 = 30 (чаш.), где 54 : 9 – количество чашек в одном наборе.
Оформляем условие в виде таблицы.

Рассуждаем.
Из первой задачи мы знаем, что в 1 наборе – 6 чашек, а всего – 60 чашек. То есть, нам известно, сколько чашек в 1 наборе и общее количество чашек, но неизвестно количество наборов. Из таблицы к задаче видно, что чтобы узнать, сколько наборов было, нужно общее количество чашек разделить на количество чашек в 1 наборе.
60 : 6 = 10 (наб.) – получится из 60 чашек.
Записываем ответ.
Ответ: в 10 наборах 60 чашек.
Вычисление выражением:
60 : (54 : 9) = 10 (наб.), где 54 : 9 - количество чашек в одном наборе.
Оформляем условие в виде таблицы.
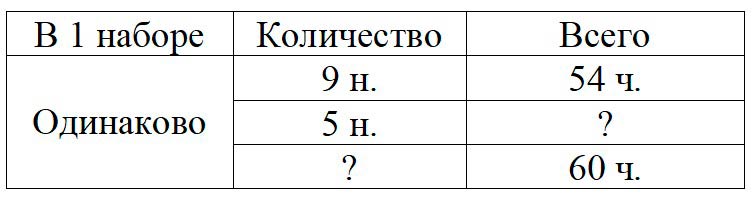
Оформляем решение по действиям.
1) 54 : 9 = 6 (чаш.) – в одном наборе.
2) 5 ∙ 6 = 30 (чаш.) – в пяти наборах.
3) 60 : 6 = 10 (наб.) – из 60 чашек.
Записываем ответ.
Ответ: в 5 наборах 30 чашек; в 10 наборах 60 чашек.
Номер 3.
В корзине было 5 кг свеклы, а в 6 одинаковых ящиках – 60 кг. Во сколько раз больше было свеклы в одном ящике, чем в корзине?
Ответ:
1) 60 : 6 = 10 (кг) – в одном ящике. 2) 10 : 5 = 2 (раза) Ответ: в 2 раза больше свёклы в ящике, чем в корзине.
1) Данная задача: вида «кол-во свеклы в 1 наборе, количество наборов, общее кол-во моркови» характеризуется зависимостями между компонентами:
Кол-во свеклы в 1 наборе ь кол-во наборов = общее кол-во свеклы.
Общее кол-во свеклы : кол-во свеклы в 1 наборе = кол-во наборов.
Общее кол-во свеклы : кол-во наборов = кол-во свеклы в 1 наборе.
2) Чтобы узнать, во сколько раз больше одно число, чем другое, нужно большее число разделить на меньшее.
Оформляем условие в виде таблицы.

Рассуждаем.
В 6 одинаковых ящиках было 60 кг свеклы. Значит, нам известно количество ящиков, общее количество свеклы, но неизвестно, сколько свеклы было в одном ящике. При этом все ящики одинаковые, т.е. в них помещается равное количество свеклы. Из таблицы видно, что чтобы узнать, сколько свеклы было в одном ящике, нужно общее количество свеклы разделить на количество ящиков.
60 : 6 = 10 (кг) – в одном ящике.
Продолжаем рассуждение.
В корзине было 5 кг свеклы, а в ящике – 10 кг. Чтобы узнать, во сколько раз больше одно число, чем другое, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз больше свеклы в ящике, чем в корзине, нужно количество свеклы в одном ящике разделить на количество свеклы в корзине.
10 : 5 = 2 (раза) – во сколько раз больше было свеклы в одном ящике, чем в корзине.
Записываем ответ.
Ответ: в 2 раза больше свёклы в ящике чем в корзине.
Решение выражением:
(60 : 6) : 5 = 2 (раза), где 60 : 6 – количество свеклы в ящике.
Номер 4.
Ответ:27 : 9 = 3 38 + 59 = 97 56 : 7 = 8 42 − 17 = 25

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Вычисляем деление.
27 : 9 = 3, так как 9 · 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
56 : 7 = 8, так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Расставляем порядок действий и выполняем вычисления.
1 2
3 · 8 : 6 = 4
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем вычисления по порядку слева направо.
1) 3 ∙ 8 = 24
2) 24 : 6 = 4, так как 6 · 4 = 24
1 2
2 · 9 : 3 = 6
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем вычисления по порядку слева направо.
1) 2 ∙ 9 = 18
2) 18 : 3 = 6, так как 3 · 6 = 18
1 3 2
21 : 3 + 0 · 6 = 7
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действия деление и умножение по порядку слева на право и последним действием сложение.
1) 21 : 3 = 7, так как 3 · 7 = 21
2) 0 ∙ 6 = 0, если число умножить на нуль, то получится нуль.
3) 7 + 0 = 7, если к числу прибавить нуль, то число не изменится.
1 3 2
27 : 3 + 1 · 6 = 15
1) 27 : 3 = 9, так как 3 · 9 = 27
2) 1 ∙ 6 = 6, если число умножить на 1, то оно не изменится.
3) 9 + 6 = 9 + (1 + 5) = (9 + 1) = 5 = 10 + 5 = 15
Число 6 представим в виде суммы чисел 1 и 5. Вначале к числу 9 прибавим число 1, а потом прибавим число 5.
Вычислим сложение и вычитание в столбик.
38 + 59 = 97
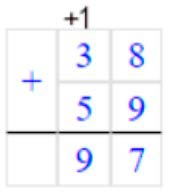
Складываем единицы. 8 + 9 = 17 – получилось 1 дес. и 7 ед.
Записываем в разряде единиц число 7, а 1 дес. запоминаем.
Складываем десятки. 3 + 5 = 8 и ещё 1 дес., который запомнили 8 + 1 = 9 – получилось десяток.
Записываем в разряде десятков число 9.
Читаем ответ: 97.
42 – 17 = 25
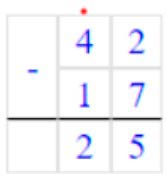
Вычитаем единицы. От числа 2 мы не можем отнять 7.
Занимаем 1 дес. = 10 ед., 10 + 2 = 12 ед., 12 – 7 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Вычитаем десятки Было 4 дес., мы занимали 1 дес, осталось 4 – 1 = 3 дес.,
3 – 1 = 2 – получилось десятков.
Записываем в разряде десятков число 2.
Читаем ответ: 25.
Оформляем задание в тетрадь.
27 : 9 = 3
56 : 7 = 8
3 · 8 : 6 = 24 : 6 = 4
2 · 9 : 3 = 18 : 3 = 6
21 : 3 + 0 · 6 = 7 + 0 = 7
27 : 3 + 1 · 6 = 9 + 6 = 15
38 + 59 = 97
42 − 17 = 25
Номер 5.
Рассмотри рисунок и скажи, во сколько раз бабочек меньше, чем стрекоз.

6 : 2 = 3 Ответ: в 3 раза бабочек меньше, чем стрекоз.
1) Сосчитай, сколько на рисунке бабочек и стрекоз.
2) Помни, чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее число.
Оформляем условие в виде краткой записи.
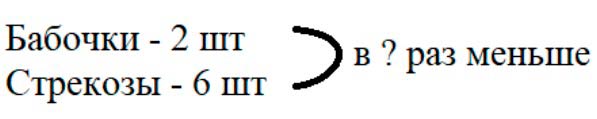
Рассуждаем.
Бабочек на рисунке 2, а стрекоз – 6 штук.
Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
Значит, чтобы узнать, во сколько раз бабочек меньше, чем стрекоз, нужно количество больших насекомых разделить на количество меньших.
6 : 2 = 3 (раза) – во сколько раз бабочек меньше, чем стрекоз.
Записываем ответ.
Ответ: в 3 раза бабочек меньше, чем стрекоз.
Задание внизу страницы
Даны числа 4, 5, 7, 8, 9. Каждое четное число уменьши в 2 раза, а нечетное увеличь в 9 раз.
Ответ:
4 : 2 = 2
8 : 2 = 4
5 ∙ 9 = 45
7 ∙ 9 = 63
9 ∙ 9 = 81
1) Четные числа – это числа, которые без остатка делятся на 2.
2) Нечетные числа – это те, которые не делятся на 2 нацело, т.е. все остальные.
3) «уменьшить в 2 раза», значит, разделить на 2.
4) «увеличить в 9 раз», значит, умножить на 3.
Рассмотрим числа.
Число 4 – чётное число, так как делится без остатка на 2.
4 : 2 = 2
Число 5 – нечетное число, так как не делится без остатка на 2.
5 : 2 = 2 (ост. 1)
Число 7 – нечетное число, так как не делится без остатка на 2.
7 : 2 = 3 (ост. 1)
Число 8 – четное число, так как делится без остатка на 2.
8 : 2 = 4
Число 9 – нечётное число, так как не делится без остатка на 2.
9 : 2 = 4 (ост. 1)
Значит,
4, 8 – чётные числа;
5, 7, 9 – нечётные числа.
Вычисляем.
Уменьшим чётные числа в 2 раза, это значит разделим их на 2.
4 : 2 = 2, так как 2 · 2 = 4,
где 2 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
8 : 2 = 4, так как 2 · 4 = 8,
где 2 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Продолжаем вычисления.
Нечётные числа увеличим в 9 раз, это значит умножим на 9.
5 · 9 = 45,
где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
Четные числа: 4 и 8.
4 : 2 = 2
8 : 2 = 4
Нечетные числа: 5, 7 и 9.
5 ∙ 9 = 45
7 ∙ 9 = 63
9 ∙ 9 = 81
Задание на полях страницы
Цепочка:

72 : 8 = 9 9 ∙ 4 = 36 36 : 6 = 6
1) Выполни действия по порядку.
2) Первая зеленая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
72 : 8 = 9, так как 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 4 = 36,
где 9 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
36 : 6 = 6, так как 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
72 : 8 = 9
9 ∙ 4 = 36
36 : 6 = 6
72 : 8 = 9 → 9 · 4 = 36 → 36 : 6 = 6
Учимся решать задачи и выполнять вычисления.
Номер 1.
Составь по таблице три задачи и реши их.


Задача 1:
Мама купила 6 конфет по 4 рубля за штуку.
Сколько заплатила мама за покупку?
6 · 4 = 24 (руб.)
Ответ: 24 рубля заплатила мама за покупку.
Задача 2:
Мама купила за 24 рубля несколько конфет. Одна конфета стоит 4 р.
Сколько конфет купила мама?
24 : 4 = 6 (к.)
Ответ: 6 конфет купила мама.
Задача 3:
Мама купила 6 конфет за 24 рубля. Сколько стоит одна конфета?
24 : 6 = 4 (руб.)
Ответ: 4 рубля стоит одна конфета.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена
Составим условие.
Мама купила 6 конфет по 4 рубля за штуку. Сколько заплатила мама за покупку?
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Мама купила 6 конфет по 4 рубля за штуку. Значит, нам известно, сколько конфет было куплено и сколько стоит одна конфета, но нам неизвестно – сколько стояли все конфеты. Общая стоимость всех конфет складывается из стоимостей всех конфет. Значит, чтобы узнать сколько стоят все конфеты, нужно сложить стоимость каждой конфеты.
Но цена конфет одинаковая, значит, за каждую конфету заплатили 4 рубля. Поэтому, сложение одинаковых слагаемых можно заменить умножением.
6 ∙ 4 = 24 (рубля) − потратила мама за 6 конфет.
Записываем ответ.
Ответ: 24 рубля заплатила мама за покупку.
Составим условие.
Мама купила за 24 рубля несколько конфет. Одна конфета стоит 4 р. Сколько конфет купила мама?
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Мама купила за 24 рубля несколько конфет, причем одна конфета стоит 4 рубля. Значит, нам известна цена конфеты и стоимость всех конфет, но неизвестно, сколько конфет купила мама. Из таблицы видно, что чтобы узнать, сколько конфет купила мама, нужно общую стоимость конфет разделить на цену конфеты.
24 : 4 = 6 (конфет) − купила мама.
Записываем ответ.
Ответ: 6 конфет купила мама.
Составим условие.
Мама купила 6 конфет за 24 рубля. Сколько стоит одна конфета?
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Мама купила 6 конфет за 24 рубля. Значит, нам известно, сколько конфет купили и сколько денег потратили, но не узнали цену одной конфеты. Из таблицы видно, что чтобы узнать. Сколько стоит одна конфета, нужно общую стоимость конфет разделить на их количество.
24 : 6 = 4 (рубля) − цена одной конфеты.
Записываем ответ.
Ответ: 4 рубля стоит одна конфета.
Номер 2.
В двух аквариумах разместили 12 рыбок так, что в одном из них рыбок было в 2 раза больше, чем в другом. Сколько рыбок в каждом аквариуме?
Выбери правильный ответ: 12 и 6; 3 и 6; 8 и 4; 10 и 5. Докажи, что он правильный.

1) 1 + 2 = 3 (ч.) - всего составляют количества рыбок в аквариумах
2) 12 : 3 = 4 (р.) - в первом аквариуме
3) 4 * 2 = 8 (р.) - во втором аквариуме
Ответ: правильный ответ 8 и 4.
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
1) 1 + 2 = 3 части всего.
2) 12 : 3 = 4 (р.) – в первом аквариуме.
3) 4 · 2 = 8 (р.) – во втором аквариуме.
Записываем ответ.
Ответ: 8 и 4, вот правильный ответ.
Номер 3.
В куске 25 м ткани. Хватит ли этой ткани, что-бы сшить 6 платьев, расходуя на каждое по 3 м ткани? Сколько метров ткани останется, если расходовать на каждое по 4 м?
Ответ:1) 6 · 3 = 18 (м) – ткани на 6 платьев. 2) 6 · 4 = 24 (м) 3) 25 – 24 = 1 (м) Ответ: да, хватит; останется 1 м, если расходовать по 4 м.
Данная задача: вида «расход ткани на 1 платье, количество платьев, общее количество ткани» характеризуется зависимостями между компонентами:
Расход ткани на 1 платье · количество платьев = общее количество ткани.
Общее количество ткани : количество платьев = расход ткани на 1 платье.
Общее количество ткани : расход ткани на 1 платье = количество платьев.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Чтобы понять, хватит ли ткани на пошив 6 пальто, расходуя на каждый по 3 метра, необходимо сначала понять, а сколько ткани потратят всего.
Нам известно количество ткани и расход ткани на 1 пальто, но неизвестно, сколько ткани израсходуют всего. При этом, общее количество ткани складывается из количества ткани, расходуемой на каждое платье. Поэтому, чтобы узнать, сколько ткани израсходовали, нужно сложить количество ткани, потраченной на каждое платье.
Но расход ткани на 1 платье одинаковое, значит, сложение одинаковых слагаемых можно заменить умножением.
6 ∙ 3 = 18 (м) − ткани нужно, чтобы сшить 6 платьев по 3 м.
Продолжаем рассуждение.
Получается, что 18 метров ткани потратили на пошив 6 одинаковых платьев. Значит, сравниваю, сколько ткани было и сколько потратили, чтобы понять, хватит ли ее.
25 м > 18 м, значит, ткани на пошив 6 платьев хватит.
Записываем ответ.
Ответ: 25 м ткани хватит на пошив 6 платьев.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Чтобы понять, сколько ткани останется после пошива платьев, нужно сначала понять, сколько ткани израсходовали на пошив 4 платьев.
Нам известен расход на 1 платье и количество платьев, но неизвестно, сколько платьев израсходовали. Из модели к задаче видно, что чтобы узнать, сколько ткани израсходовали на 4 платья, нужно сложить ткани, расходуемое на каждое платье.
Но расход ткани на 1 платье одинаковый, значит, сложение одинаковых слагаемых можно заменить умножением. Тогда, чтобы узнать, сколько ткани потратили, можно расход ткани на 1 платье умножить на количество платьев. Вычисляется умножением.
6 ∙ 4 = 24 (м) – ткани нужно, чтобы сшить 6 платьев по 4 м на каждое.
Продолжаем рассуждение.
Значит, израсходовали 24 метра ткани. Мы знаем, что общее количество ткани складывается из количества израсходованной ткани и оставшейся. Поэтому, чтобы узнать, сколько ткани осталось, нужно из общего количества ткани вычесть количество потраченной.
25 − 24 = 1 (м) − ткани останется, если расходовать на каждое платье по 4 м.
Записываем ответ.
Ответ: 25 м ткани хватит на пошив 6 платьев по 4 м.
Решение выражением:
25 – (4 · 6),где 4 · 6 – количество потраченной ткани на 6 платьев.
Номер 4.
72 – 32 : 4 64 – 16 : 8 + 8 9 · (13 – 9) 36 – 18 : 2 64 – 16 : (8 + 8) 6 · (27 – 20)
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий.
2 1
72 − 32 : 4 = 64
В данном выражении присутствуют действия вычитание и деление. В начале выполним действие деление, а потом вычитание.
2 1
36 − 18 : 2 = 27
В данном выражении присутствуют действия вычитание и деление. В начале выполним действие деление, а потом вычитание.
2 1 3
64 − 16 : 8 + 8 = 70
В данном выражении присутствуют действия сложение, вычитание и деление. В начале выполним действие деление, потом вычитание и последним действием сложение.
3 2 1
64 − 16 : (8 + 8) = 63
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. В начале выполним действие в скобках - сложение, потом деление и последним действием вычитание.
2 1
9 · (13 − 6) = 63
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
6 · (27 − 20) = 42
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
Вычислим по действиям.
2 1
72 − 32 : 4 = 64
1) 32 : 4 = 8, так как 4 · 8 = 32
2) 72 − 8 = 72 – (2 + 6) = (72 – 2) – 6 = 70 – 6 = 64
Представим число 8 в виде суммы чисел 2 и 6. В начале из числа 72 вычтем число 2, а потом вычтем число 6.
2 1
36 − 18 : 2 = 27
1) 18 : 2 = 9, так как 2 · 9 = 18
2) 36 − 9 = 36 – (6 + 3) = (36 – 6) – 3 = 30 – 3 = 27
Представим число 9 в виде суммы чисел 6 и 3. В начале из числа 36 вычтем число 6, а потом вычтем число 3.
2 1 3
64 − 16 : 8 + 8 = 70
1) 16 : 8 = 2, так как 8 · 2 = 16
2) 64 – 2 = 62
3) 62 + 8 = 70
3 2 1
64 − 16 : (8 + 8) = 63
1) 8 + 8 = 16
2) 16 : 16 = 1, если число разделить на само себя, то получится 1.
3) 62 + 1 = 63
2 1
9 · (13 − 6) = 63
1) 13 – 6 = 7
2) 9 ∙ 7 = 63
2 1
6 · (27 − 20) = 42
1) 27 – 20 = 7
2) 6 ∙ 7 = 42
Оформляем задание в тетрадь.
72 – 32 : 4 = 72 – 8 = 64
36 – 18 : 2 = 36 – 9 = 27
64 – 16 : 8 + 8 = 64 – 2 + 8 = 62 + 8 = 70
64 – 16 ∶ (8 + 8) = 64 – 16 : 16 = 64 – 1 = 63
9 · (13 – 6) = 9 · 7 = 63
6 · (27 – 20) = 6 · 7 = 42
Номер 5.
4 м 9 дм = ▢ дм 1 дм2 = ▢ см2 3 дм 4 см = ▢ см 1 м2 = ▢ дм2
Ответ:4 м 9 дм = 49 дм 1 дм2 = 100 см2 3 дм 4 см = 34 см 1 м2 = 100 дм2
Помни о соотношении числовых значений единиц длины и площади.
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм
1 м = 100 см
1 дм2 = 100 см2
1 м2 = 100 дм2
Рассмотрим выражения.
4 м 9 дм = 40 дм + 9 дм = 49 дм, так как 1 м = 10 дм.
3 дм 4 см = 30 см + 4 см = 34 см, так как 1 дм = 10 см.
1 дм2 = 10 см · 10 см = 100 см2, так как 1 дм = 10 см.
1 м2 = 10 дм · 10 дм = 100 дм2, так как 1 м = 10 дм.
Оформляем задание в тетрадь.
4 м 9 дм = 4 ∙ 10 дм + 9 дм = 49 дм
3 дм 4 см = 3 ∙ 10 см + 4 см = 34 см
1 дм2 = 10 см ∙ 10 см = 100 см2
1 м2 = 10 дм ∙ 10 дм = 100 дм2
Номер 6.
В парке разбили две клумбы. Одна клумба имела форму квадрата с длиной стороны 3 м, а другая — форму прямоугольника, длины сторон которого 4 м и 2 м. У какой клумбы площадь больше? Что можно сказать про их периметры?
Ответ:
Площадь первой клумбы больше.
Периметры одинаковые.
У какой клумбы площадь больше?
1) 3 · 3 = 9 (м2) – площадь первой клумбы.
2) 4 · 2 = 8 (м2) – площадь второй клумбы.
Ответ: Площадь первой клумбы больше.
Что можно сказать про их периметры?
1) 3 · 4 = 12 (м) – периметр первой клумбы.
2) 4 · 2 + 2 · 2 = 12 (м) – периметр второй клумбы.
Ответ: Периметры одинаковые.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Чтобы вычислить площадь квадрата, нужно длину стороны умножить на сторону.
3) Периметр фигуры – суммы длин всех ее сторон.
Оформляем условие в виде краткой записи.
-(2023).jpg)
АВКС – квадрат.
Длина – 3 м
Ширина – 3 м
Площадь – ?
Периметр – ?
-(2023).jpg)
СТКР – прямоугольник.
Длина – 2 м
Ширина – 4 м
Площадь – ?
Периметр – ?
Рассуждаем.
Чтобы вычислить площадь прямоугольника, нужнонайти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
3 м · 3 м = 9 (м2) – площадь квадрата.
4 м · 2 м = 8 (м2) – площадь прямоугольника.
Сравним площади:
9 м2 > 8 м2 – площадь первой клумбы больше, площади второй клумбы.
Найдём периметр квадрата.
Квадрат – замкнутая ломаная. Длина ломаной равна сумме длин всех отрезков-звеньев, значит, длина квадрата – сумма длин всех его сторон.
Получается, чтобы узнать, каков периметр квадрата, нужно сложить длины всех его сторон.
Но у квадрата все стороны равны. Значит, сложение одинаковых слагаемых можно заменить умножением. поэтому, чтобы вычислить периметр квадрата, нужно длину стороны квадрата умножить на их количество.
3 м · 4 = 12 (м) – периметр квадрата.
Найдём периметр прямоугольника
Способ 1:
сложить все стороны.
Способ 1: сложить все стороны. 4 + 4 + 2 + 2 = (4 + 2) + (4 + 2) = 6 + 6 = 12 (м)
Споосб 2: поотдельности длину и ширину умножить на 2, а потом полученные произвдения сложить.
4 · 2 + 2 · 2 = 8 + 4 = 12 (м)
Споосб 3: сложить длину и ширину и полученную сумму умножить на 2.
(4 + 2) · 2 = 6 · 2 = 12 (м)
Сравним периметры:
12 м = 12 м – периметры клумб одинаковые.
Оформим задание в тетрадь.
1) 3 ∙ 3 = 9 (м2) − площадь квадратной клумбы.
2) 4 ∙ 2 = 8 (м2) − площадь прямоугольной клумбы.
3) 9 > 8 − значит, площадь квадратной клумбы больше.
4) 3 ∙ 4 = 12 (м) − периметр квадратной клумбы.
5) (4 + 2) ∙ 2 = 12 (м) − периметр прямоугольной клумбы;
6) 12 = 12 − значит, площади клумб равны.
Ответ: площадь квадратной клумбы больше; периметры клумб равны.
Номер 7.
Определи, как можно, не изменяя чисел, сделать равенства верными. Выполни это.
16 + 20 : 4 = 9 9 · 10 – 7 = 27 15 + 36 : 9 – 3 = 21
Ответ:
1) Перебирай все возможные варианты, пока не найдешь, верное решение.
2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставим скобки и порядок действий.
1 2
(16 + 20) : 4 = 9
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполним действие в скобках – сложение, а потом действие вне скобок – деление.
2 1
9 · (10 − 7) = 27
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом действие вне скобок – умножение.
3 2 1
15 + 36 : (9 − 3) = 21
В данном выражении присутствуют действия слоение, вычитание и деление, а также скобки. В начале выполним действие в скобках – вычитание, потом действие деление и последним действием – сложение.
Вычисли по действиям.
1 2
(16 + 20) : 4 = 9
1) 16 + 20 = 30
2) 36 : 4 = 9, так как 4 · 9 = 36
2 1
9 · (10 − 7) = 27
1) 10 – 7 = 3
2) 9 ∙ 3 = 27
3 2 1
15 + 36 : (9 − 3) = 21
1) 9 – 3 = 6
2) 36 : 6 = 6, так как 6 · 6 = 36
3) 15 + 6 = 21
Оформим задание в тетрадь.
(16 + 20) : 4 = 36 : 4 = 9
9 ∙ (10 – 7) = 9 · 3 = 27
15 + 36 : (9 – 3) = 15 + 36 : 6 = 15 + 6 = 21
Задание в низу страницы.
В палатке было 8 ящиков огурцов, по 10 кг в каждом. До обеденного перерыва продали 54 кг. Сколько килограммов огурцов осталось?
Ответ:Привезли – 8 ящ. по 10 кг Продали – 54 кг Осталось – ? кг 1) 10 · 8 = 80 (кг) – привезли. 2) 80 – 54 = 26 (кг) Ответ: осталось 26 кг огурцов.
Данная задача: вида «вместимость 1 ящика, количество ящиков, общее количество огурцов» характеризуется зависимостями между компонентами:
Вместимость 1 ящика · количество ящика = общее количество огурцов.
Общее количество огурцов : вместимость 1 ящика = количество ящиков.
Общее количество огурцов : количество ящиков = вместимость 1 ящика.
Оформляем условие в виде краткой записи.
Привезли – 8 ящ. по 10 кг
Продали – 54 кг
Осталось – ? кг
Рассуждаем.
В палатку привезли 8 ящиков огурцов по 10 кг в каждом. Значит, нам известно сколько огурцов в одном ящике, количество ящиков, но неизвестно, сколько всего было огурцов. При этом, общее количество огурцов складывается из количества огурцов в каждом ящике. Поэтому, чтобы узнать, сколько огурцов было всего, нужно сложить количество огурцов каждого ящика.
Но количество огурцов каждого ящика одинаковое, поэтому сложение одинаковых слагаемых можно заменить умножением. получается, нужно количество огурцов одного ящика умножить на количество ящиков.
10 ∙ 8 = 80 (кг) – привезли.
Продолжаем рассуждение.
Общее количество огурцов в палатке складывается из количества огурцов, которые продали и которые остались. Значит, чтобы узнать, сколько огурцов осталось, нужно из общего количества огурцов вычесть количество проданного.
80 − 54 = 26 (кг) – осталось.
Записываем ответ.
Ответ: осталось 26 кг огурцов.
Решение выражением:
10 · 8 – 54, где 10 · 8 – количество огурцов, которые были в палатке.
Задание на полях страницы.


Проверка:
Первый магический квадрат:
28 + 20 + 12 = 40 + 20 = 60
18 + 16 + 26 = 34 + 26 = 60
14 + 24 + 22 = 38 + 22 = 60
22 + 12 + 26 = 34 + 26 = 60
24 + 20 + 16 = 20 + 40 = 60
14 + 28 + 18 = 14 + 46 = 60
20 + 26 + 14 = 20 + 40 = 60
18 + 20 + 22 = 20 + 40 = 60
Второй магический квадрат:
21 + 28 + 23 = 44 + 28 = 72
26 + 24 + 22 = 50 + 22 = 72
25 + 20 + 27 = 20 + 52 = 72
21 + 26 + 25 = 46 + 26 = 72
28 + 24 + 20 = 52 + 20 = 72
23 + 22 + 27 = 50 + 22 = 72
21 + 24 + 27 = 45 + 27 = 72
25 + 24 + 23 = 49 + 23 = 72
Магический квадрат – квадрат, в котором числа, стоящие на одной прямой по горизонтали, вертикали и диагонали в сумме образуют одинаковое число.
Найдём магическую сумму.
-(2023).jpg)
28 + 20 + 12 = 60 – магическая сумма.
Значит, в данном магическом квадрате по горизонтали, вертикали и диагонали сумма цифр должна равняться 60.
ассмотрим третий столбец.
В столбце не достает первого числа.
+ 12 + 22 = 60
Упростим выражение сложив числа 12 и 22.
+ 34 = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 34 = 26 – недостающее число во третьем столбике.
-(2023).jpg)
Рассмотрим диагональ.
В диагонали не достает первого числа.
+ 20 + 22 = 60
Упростим выражение сложив числа 20 и 22.
+ 42 = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 42 = 18 – недостающее число по диагонали.
-(2023).jpg)
Рассмотрим первую строчку.
В строчке не достает второго числа.
18 + + 26 = 60
Упростим выражение сложив числа 18 и 26.
44 + = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 44 = 16 – недостающее число в первой строчке.
-(2023).jpg)
Рассмотрим первый столбик.
В столбике не достает третьего числа.
18 + 28 + = 60
Упростим выражение сложив числа 18 и 28.
46 + = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 46 = 14 – недостающее число в первом столбике.
-(2023).jpg)
Рассмотрим второй столбик.
В столбике не достает третьего числа.
16 + 20 + = 60
Упростим выражение сложив числа 16 и 20.
36 + = 60
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
60 – 36 = 24 – недостающее число во втором столбике.
-(2023).jpg)
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 60.
Найдём магическую сумму.
-(2023).jpg)
21 + 24 + 27 = 72 – магическая сумма.
Значит, в данном магическом квадрате по горизонтали, вертикали и диагонали сумма цифр должна равняться 72.
Рассмотрим первую строчку.
В строчке не достает второго числа.
21 + + 23 = 72
Упростим выражение сложив числа 21 и 23.
44 + = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 44 = 28 – недостающее число в первой строчке.
-(2023).jpg)
Рассмотрим третий столбик.
В столбике не достает второго числа.
23 + + 27 = 72
Упростим выражение сложив числа 23 и 27.
50 + = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 50 = 22 – недостающее число в третьем столбике.
-(2023).jpg)
Рассмотрим вторую строчку.
В столбике не достает первого числа.
+ 24 + 22 = 72
Упростим выражение сложив числа 24 и 22.
46 + = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 46 = 26 – недостающее число во второй строке.
-(2023).jpg)
Рассмотрим первый столбик.
В столбике не достает третьего числа.
21 + 26 + = 72
Упростим выражение сложив числа 21 и 26.
47 + = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 47 = 25 – недостающее число в первом столбике.
-(2023).jpg)
Рассмотрим второй столбик.
В столбике не достает третьего числа.
28 + 24 + = 72
Упростим выражение сложив числа 28 и 24.
52 + = 72
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
72 – 52 = 20 – недостающее число во втором столбике.
-(2023).jpg)
Получившийся квадрат – магический, так как сумма чисел по диагонали, по горизонтали и по вертикали равна одному числу 72.
Делаем вывод.
Вывод: оба квадрата магические. В первом квадрате значение суммы равно 60, а во втором – 72.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.