Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 67

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 4.
Из 12 м ткани портной сшил 6 одинаковых детских костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?
Ответ:
1) 12 : 6 = 2 (м) – ткани на один костюм. 2) 2 ∙ 10 = 20 (м) – ткани на 10 костюмов. 3) 2 ∙ 7 = 14 (м) – ткани на 7 костюмов. Ответ: 20 м ткани необходимо на пошив 10 костюмов; 14 м ткани необходимо на пошив 7 костюмов.
Данная задача: вида «расход ткани на 1 костюм, количество костюмов, общее количество ткани» характеризуется зависимостями между компонентами:
Расход ткани на 1 костюм · количество костюмов = общее количество ткани.
Общее количество ткани : расход ткани на 1 костюм = количество костюмов.
Общее количество ткани : количество костюмов = расход ткани на 1 костюм.
Оформляем условие в виде таблицы.

Рассуждаем.
Из 12 метров ткани сшили 6 одинаковых костюмов. Одинаковых, значит на каждый костюм расходовали равное количество ткани. Нам известно количество костюмов, общее количество ткани, но неизвестен расход. Значит, чтобы узнать, каков расход ткани на 1 костюм, нужно общее количество ткани разделить на количество костюмов.
12 : 6 = 2 (м) – ткани потребуется на один костюм.
Продолжаем рассуждение.
Мы узнали, что расход ткани на 1 костюм – 2 метра. Нам нужно узнать, сколько метров ткани израсходовали на пошив 10 костюмов. Общее количество потраченной ткани складывается из количества ткани, расходуемой на каждый костюм. Значит, чтобы узнать, сколько ткани израсходовали всего, нужно сложить количество ткани, потраченной на каждый костюм.
Но количество ткани, расходуемое на каждый костюм одинаковое, значит, сложение одинаковых слагаемых можно заменить умножением.
2 ∙ 10 = 20 (м) – ткани потребуется на 10 костюмов.
Продолжаем рассуждение.
Аналогично вычисляем количество израсходованной ткани на 7 костюмов.
Количество ткани, расходуемое на 1 костюм, умножаем на количество костюмов.
2 ∙ 7 = 14 (м) – ткани потребуется на 7 костюмов.
Записываем ответ.
Ответ: 20 м ткани потребуется на 10 костюмов; 14 м ткани потребуется на 7 костюмов.
Номер 5.
Для ремонта квартиры купили 4 банки краски, по 3 кг каждая. Сколько килограммов краски купили?
Составь две обратные задачи и реши их.

4 ∙ 3 = 12 (кг)
Ответ: 12 кг краски купили.
Обратная задача 1:
Для ремонта квартиры купили 12 кг краски в 4 одинаковых банках.
Сколько килограммов краски в одной банке?
12 : 4 = 3 (кг)
Ответ: 3 кг краски в одной банке.
Обратная задача 2:
Для ремонта квартиры купили 12 кг краски по 3 кг в каждой.
Сколько банок краски купили?
12 : 3 = 4 (б.)
Ответ: купили всего 4 банки краски.
Данная задача: вида «масса 1 банки, количество банок, масса всех банок» характеризуется зависимостями между компонентами:
Масса 1 банки · количество банок = масса всех банок.
Масса всех банок : масса 1 банки = количество банок.
Масса всех банок : количество банок = масса 1 банки.
Оформляем условие в виде таблицы.

Рассуждаем.
Купили 4 банки краски по 3 кг каждая. Значит, нам известна масса 1 банки краски, количество банок, но неизвестная общая масса всех банок. Общая масса банок складывается из количества краски в каждой из банок.
Значит, чтобы узнать, сколько краски было всего, нужно сложить количество банок в каждой банки.
Но масса краски в 1 банке одинаковая, поэтому сложение одинаковых слагаемых можно заменить умножением.
4 ∙ 3 = 12 (кг) – всего краски купили.
Записываем ответ.
Ответ: 12 кг краски купили.
Составляем условие.
Для ремонта квартиры купили 12 кг краски в 4 одинаковых банках. Сколько килограммов краски в одной банке?
Оформляем условие в виде таблицы.

Рассуждаем.
Купили несколько банок по 3 кг каждая, а общая масса банок – 12 кг. Но неизвестно, сколько банок купили. Значит, чтобы узнать, сколько банок купили, нужно общую масса краски во всех банках разделить на массу 1 банки.
12 : 4 = 3 (кг) – краски в одной банке.
Записываем ответ.
Ответ: 3 кг краски в каждой банке.
Составляем условие.
Для ремонта квартиры купили 12 кг краски по 3 кг в каждой. Сколько банок краски купили?
Оформляем условие в виде таблицы.

Рассуждаем.
Купили 4 банки так, что масса краски во всех банках – 12 кг, а масса одной банки – неизвестна. Поэтому, чтобы узнать, сколько кг краски помещается в одной банке, нужно общую массу краски во всех банках разделить на количество банок.
12 : 3 = 4 (б.) – купили всего краски.
Записываем ответ.
Ответ: 4 банки краски купили.
Номер 6.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий.
2 1
9 ∙ (38 − 30) = 72
В выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.
2 1
65 − (49 − 19) = 35
В данном выражении присутствуют действия вычитания, а также скобки. Вначале выполняем действие вычитание в скобках, а потом вычитание вне скобок.
2 1
28 + 45 : 5 = 37
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.
1 3 2
8 ∙ 7 + 5 ∙ 6 = 86
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а потом сложение.
1 3 2
9 ∙ 9 − 28 : 7 = 77
В данном выражении присутствуют действия вычитание, умножение и деление. Вначале выполняем умножение и деление по порядку слева направо, а последним действием – вычитание.
1 3 2
63 : 7 + 54 : 6 = 18
В данном выражении присутствуют действия сложение и деления. Вначале выполняем действия деления по порядку слева направо, а потом сложение.
2 1
7 ∙ (100 − 91) = 63
В выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.
2 1
6 ∙ (75 − 65) = 60
В выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.
2 1
7 + 36 : 4 = 16
В данном выражении присутствуют действия сложение и деление. Вначале выполняем действие деление, а потом сложение.
Выполняем вычисления по действиям.
2 1
9 ∙ (38 − 30) = 72
1) 38 – 30 = 8
2) 9 ∙ 8 = 72
2 1
65 − (49 − 19) = 35
1) 49 – 19 = 30
2) 65 − 30 = 35
2 1
28 + 45 : 5 = 37
1) 45 : 5 = 9
2) 28 + 9 = 37
1 3 2
8 ∙ 7 + 5 ∙ 6 = 86
1) 8 ∙ 7 = 56
2) 5 ∙ 6 = 30
3) 56 + 30 = 86
1 3 2
9 ∙ 9 − 28 : 7 = 77
1) 9 ∙ 9 = 81
2) 28 : 7 = 4
3) 81 − 4 = 77
1 3 2
63 : 7 + 54 : 6 = 18
1) 63 : 7 = 9
2) 54 : 6 = 9
3) 9 + 9 = 18
2 1
7 ∙ (100 − 91) = 63
1) 100 – 91 = 9
2) 7 ∙ 9 = 63
2 1
6 ∙ (75 − 65) = 60
1) 76 – 65 = 10
2) 6 ∙ 10 = 60
2 1
7 + 36 : 4 = 16
1) 36 : 4 = 9
2) 7 + 9 = 16
Оформляем задание в тетрадь.
9 · (38 – 30) = 9 · 8 = 72
65 – (49 – 19) = 65 – 30 = 35
(28 + 2) + 7 = 30 + 7 = 37
8· 7 + 5 · 6 = 56 + 30 = 86
9 · 9 – 28 : 7 = 81 – 4 = 77
63 : 7 + 54 : 6 = 9 + 9 = 18
7 · (100 – 91) = 7 · 9 = 63
6 · (75 – 65) = 6 · 10 = 60
7 + 36 : 4 = 7 + 9 = 16
Номер 7.
Коля, Дима и Саша собрали вместе 30 грибов. Дима нашел в 2 раза больше грибов, чем Коля, а Коля – в 3 раза меньше, чем Саша. Сколько грибов нашел каждый из них? Сделай чертеж к задаче и реши ее.
Ответ:
Коля собрал – 1 часть грибов Дима – собрал 2 части грибов Саша – собрал 3 части грибов
1-й способ решения: 1) 1 + 2 + 3 = 6 (ч.) - сколько всего равных частей грибов собрали ребята 2) 30 : 6 = 5 (г.) – столько грибов собрал Коля или сколько грибов приходится на 1 часть 3) 5 ∙ 2 = 10 (г.) – столько грибов собрал Дима или сколько грибов приходится на 2 части 4) 5 ∙ 3 = 15 (г.) – столько грибов собрал Саша или сколько грибов приходится на 3 части Ответ: Саша - 15 грибов, Дима - 10 грибов, Коля - 5 грибов.
2-й способ решения:
Сколько всего равных частей грибов собрали ребята?
1 + 2 + 3 = 6 (ч.)
Сколько грибов приходится на 1 часть?
30 : 6 = 5 (г.) – столько грибов собрал Коля.
Сколько грибов приходится на 2 части?
5 ∙ 2 = 10 (г.) – столько грибов собрал Дима.
Сколько грибов приходится на 3 части?
5 ∙ 3 = 15 (г.) – столько грибов собрал Саша.
Ответ: Саша собрал 15 грибов, Дима собрал 10 грибов, Коля собрал 5 грибов.
1) «в 2 раза больше», значит, вычисляется умножением.
2) «в 3 раза меньше», значит, вычисляется делением.
3) Составив схематический чертеж, определи, сколько всего равных частей грибов собрали ребята.
Оформляем условие в виде чертежа.
Дима нашел в 2 раза больше грибов, чем Коля, а Коля – в 3 раза меньше, чем Саша.
Значит, Дима = Коля · 2, Коля = Саша : 3, значит, а Саша = Коля · 3.
Получается схематический чертеж, где количество грибов, собранных Колей – это 1 часть, тогда на Диму приходится 2 части, а на Сашу – 3.
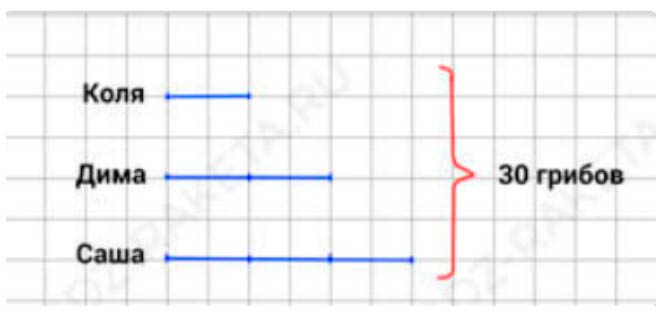
Рассуждаем.
Общее количество одинаковых частей грибов складывается из количества равных частей, приходящихся на каждого мальчика. Значит, чтобы узнать, сколько всего равных частей грибов собрали, нужно сложить количество частей каждого мальчика.
1 + 2 + 3 = 6 (ч.) – сколько всего равных частей грибов собрали ребята.
Продолжаем рассуждение.
Мы узнали, что всего равных частей грибов собрали 6. Теперь необходимо узнать, сколько грибов составляет каждая часть, если бы все мальчики собрали поровну грибов. Для этого нужно общее количество грибов разделить на количество равных частей.
30 : 6 = 5 (г.) – столько грибов собрал Коля или сколько грибов приходится на 1 часть.
Продолжаем рассуждение.
Одна часть состоит из 5 грибов, это то, сколько грибов собрал Коля. Дима собрал в 2 раза больше, чем Дима. Значит, чтобы узнать, сколько грибов собрал Дима, нужно количество грибов, собранных Колей умножить на 2.
5 ∙ 2 = 10 (г.) – столько грибов собрал Дима или сколько грибов приходится на 2 части.
Продолжаем рассуждение.
Коля собрал в 3 раза меньше, чем Саша, значит, Саша собрал в 3 раза больше, чем Коля. Поэтому, чтобы узнать, сколько грибов собрал Саша, нужно количество грибов Коли умножить на 3.
5 ∙ 3 = 15 (г.) – столько грибов собрал Саша или сколько грибов приходится на 3 части.
Записываем ответ.
Ответ: Саша собрал 15 грибов, Дима собрал 10 грибов, Коля собрал 5 грибов.
Номер 8.
В альбоме для раскрашивания было 25 рисунков. В первый день Оля раскрасила несколько рисунков, во второй – на 3 рисунка больше, чем в первый. После этого 18 рисунков остались нераскрашенными. Сколько рисунков Оля раскрасила в первый день?
Ответ:1) 25 − 18 = 7 (рис.) – раскрасила Оля за два дня. 2) 7 − 3 = 4 (рис.) – разница. 3) 4 : 2 = 2 (рис.) – раскрасила Оля в первый день. Ответ: 2 рисунка раскрасила Оля в первый день.
1) «на 3 рисунка больше», значит, вычисляется сложением.
2) Вспомни состав числа 7.
Оформляем условие в виде краткой записи.
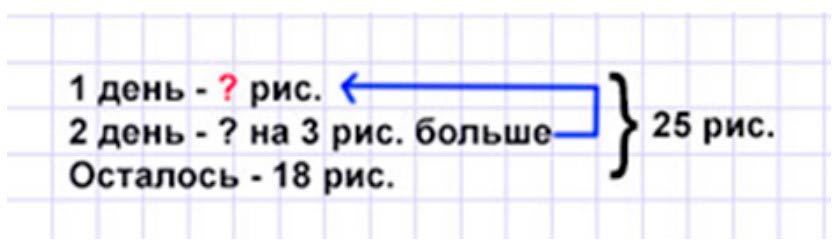
Рассуждаем.
Общее количество рисунков, сделанных в альбоме для раскрашивания, складывается из количества рисунков, сделанных за два дня и оставшихся. Поэтому, чтобы узнать, сколько рисунков было сделано за два дня, нужно из общего количества рисунков вычесть количество оставшихся.
25 − 18 = 7 (р.) − раскрасила за 2 дня.
Продолжаем рассуждение.
Мы узнали, что за два дня было сделано 7 рисунков. При этом во второй день было собрано на 3 рисунка больше, чем в первый. Вспомним состав числа 7, чтобы подобрать такие числа, при сложении которых получается 7, а одно число на 3 больше другого.
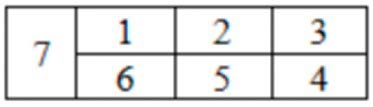
Из всех пар подходит только одна пара подходит – это числа 2 и 5, потому что 2 + 5 = 7, а 5 на 3 больше 2.
Соответственно, в первый день было сделано 2 рисунка, а во второй – 7 рисунка.
Записываем ответ.
Ответ: 2 рисунка раскрасила Оля в первый день.
Номер 9.
Расставь скобки так, чтобы равенства были верными.
Ответ:
Перебирай все возможные варианты, пытайся найти верное решение.
Расставим скобки и порядок действий.
1 2 3
(7 + 2) ∙ 9 − 4 = 77
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – сложение, потом умножение и третьим действием – вычитание.
3 2 1
7 + 2 ∙ (9 − 4) = 17
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, потом умножение и третьим действием – сложение.
3 2 1
9 + 18 : (3 + 6) = 11
В данном выражении присутствуют действия сложения и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и третьим действием – сложение вне скобок.
1 2 3
(9 + 18) : 3 + 6 = 15
В данном выражении присутствуют действия сложения и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и третьим действием – сложение вне скобок.
Вычислим по действиям.
1 2 3
(7 + 2) ∙ 9 − 4 = 77
1) 7 + 2 = 9
2) 9 ∙ 9 = 81
3) 81 − 4 = 77
3 2 1
7 + 2 ∙ (9 − 4) = 17
1) 9 – 4 = 5
2) 2 ∙ 5 = 10
3) 7 + 10 = 17
3 2 1
9 + 18 : (3 + 6) = 11
1) 3 + 6 = 9
2) 18 : 9 = 2
3) 9 + 2 = 11
1 2 3
(9 + 18) : 3 + 6 = 15
1) 9 + 18 = 27
2) 27 : 3 = 9
3) 9 + 6 = 15
Оформим задание в тетрадь.
(7 + 2) · 9 – 4 = 9 · 9 – 4 = 81 – 4 = 77
7 + 2 · (9 – 4) = 7 + 2 · 5 = 7 + 10 = 17
9 + 18 : (3 + 6) = 9 + 18 : 9 = 9 + 2 = 11
(9 + 18) : 3 + 6 = 27 : 3 + 6 = 9 + 6 = 15
Задание внизу страницы
Найди площадь листа картона квадратной формы, длина стороны которого 7 дм.
Ответ:а = 7 дм b = 7 дм S = ? дм2 S = a ∙ b S = 7 ∙ 7 S = 49 (дм2) Ответ: площадь квадратного листа картона составляет 49 дм2.
1) Площадь фигуры измеряется в квадратных сантиметрах или квадратных дециметрах.
2) Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
Оформляем условие в виде краткой записи.
.jpg)
Длина – 7 дм
Ширина – 7 дм
Площадь – ?
Рассуждаем.
Чтобы вычислить площадь прямоугольника, нужнонайти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
7 ∙ 7 = 49 (дм2) – площадь квадрата
Записываем ответ.
Ответ: площадь листа картона равна 49 дм2.
Задание на полях страницы
Ребусы:


Вспомни названия компонентов действия сложения и вычитанием, а также – зависимость между компонентами и результатами действий сложения и вычитания.
Рассуждаем.
Количество единиц вычитаемого неизвестно, но узнать количесвто единиц вычитаемого можно, если из единиц уменьшаемого вычесть единицы значения разности.
Из 7 нельзя вычесть 9, значит у десятков уменьшаемого занимаем единицу, тогда 1 дес. + 7 ед. = 17 ед.
17 ед. – 9 ед. = 8 ед.
В вычитаемом 8 единиц.
Продолжаем рассуждение.
Количесвто десятков уменьшаемого неизвестно, но количесвто десятков уменьшаемого можно узнать, если сложить количество десятков вычитаемого и значение разности.
Значит, 3 дес. + 5 дес. = 8 дес. и ещё 1 дес., который занимали при вычислении единиц. 8 дес. + 1 дес. = 9 дес.
В уменьшаемом 9 десятков.
Записываем ответ.
Получим равенство: 97 – 38 = 59.
Запишем равенство в столбик:
.jpg)
Рассуждаем.
В равенстве неизвестно первое слагаемое. Но известно второе слагаеоме и значение суммы. Значит, чтобы найти первое слагаемое, нужно из значение суммы вычесть второе слагаемое.
Значит, 84 – 57 = 27
Первое слагаемое – 27.
Записываем ответ.
Получим равенство: 27 + 57 = 84.
Запишем равенство в столбик:
.jpg)
Номер 4.
94 – 42 : 6 30 – 12 : 3 + 3 8 · (13 – 7) 75 + 81 : 9 30 – 12 : (3 + 3) 9 · (14 – 6) 38 – 64 : 8 (30 – 12) : 3 + 3 7 · (12 – 3)
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Расставляем порядок действий.
2 1
94 − 42 : 6 = 87
В данном выражении присутствуют действия деление и вычитание. Вначале выполним действие деление, а потом вычитание.
2 1
75 + 81 : 9 = 84
В данном выражении присутствуют действия деление и сложение. Вначале выполним действие деление, а потом сложение.
2 1
38 − 64 : 8 = 30
В данном выражении присутствуют действия деление и вычитание. Вначале выполним действие деление, а потом вычитание.
2 1 3
30 − 12 : 3 + 3 = 29
В данном выражении присутствуют действия сложение, вычитание и деление. Вначале выполним действие деление, потом вычитание и последним действием сложение.
3 2 1
30 − 12 : (3 + 3) = 28
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
1 2 3
(30 − 12) : 3 + 3 = 9
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – сложение.
2 1
8 · (13 − 7) = 48
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
9 · (14 − 6) = 72
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
2 1
7 · (12 − 3) = 63
В данном выражении присутствуют действия вычитание и умножение, а также скобки. вначале выполняем действие в скобках – вычитание, а потом действие вне скобок – умножение.
Вычисляем по действиям.
2 1
94 − 42 : 6 = 87
1) 42 : 6 = 7, так как 6 · 7 = 42
2) 94 − 7 = 94 – (4 + 3) = (94 – 4) – 3 = 90 – 3 = 87
Число 7 представим в виде суммы чисел 4 и 3. Вначале из числа 94 вычтем число 7, а потом вычтем число 3.
2 1
75 + 81 : 9 = 84
1) 81 : 9 = 9, так как 9 · 9 = 81
2) 75 + 9 = 75 + (5 + 4) = (75 + 5) + 4 = 80 + 4 = 84
Число 9 представим в виде суммы чисел 5 и 4. Вначале к числу 75 прибавим число 5, а потом прибавим число 4.
2 1
38 − 64 : 8 = 30
1) 64 : 8 = 8, так как 8 · 8 = 64
2) 38 − 8 = 30 + (8 – 8) = 30
2 1 3
30 − 12 : 3 + 3 = 29
1) 12 : 3 = 4, так как 3 · 4 = 12
2) 30 — 4 = 26
3) 26 + 3 = 29
3 2 1
30 − 12 : (3 + 3) = 28
1) 3 + 3 = 6
2) 12 : 6 = 2, так как 6 · 2 = 12
3) 30 — 2 = 28
1 2 3
(30 − 12) : 3 + 3 = 9
1) 30 — 12 = 18
2) 18 : 3 = 6, так как 3 · 6 = 18
3) 6 + 3 = 9
2 1
8 · (13 − 7) = 48
1) 13 – 7 = 13 – (3 + 4) = (13 – 3) – 4 = 10 – 4 = 6
Число 7 представим в виде суммы чисел 3 и 4. Вначале из числа 13 вычтем число 3, а потом вычтем число 4.
2) 8 ∙ 6 = 48
2 1
9 · (14 − 6) = 72
1) 14 – 6 = 14 – (4 + 2) = (14 – 4) – 2 = 10 – 2 = 8
Число 6 представим в виде суммы чисел 4 и 2. Вначале из числа 14 вычтем число 4, а потом вычтем число 2.
2) 9 ∙ 8 = 72
2 1
7 · (12 − 3) = 63
1) 12 – 3 = 12 – (2 + 1) = (12 – 2) – 1 = 10 – 1 = 9
Представим число 3 в виде суммы чисел 2 и 1. Вначале из числа 12 вычтем число 2, а потом вычтем число 1.
2) 7 ∙ 9 = 63
Оформляем задание в тетрадь.
94 – 42 : 6 = 94 – 7 = 87
75 + 81 : 9 = 75 + 9 = 84
38 – 64 : 8 = 38 – 8 = 30
30 – 12 : 3 + 3 = 30 – 4 + 3 = 26 + 3 = 29
30 – 12 : (3 + 3) = 30 – 12 : 6 = 30 – 2 = 28
(30 – 12) : 3 + 3 = 18 : 3 + 3 = 6 + 3 = 9
8 · (13 – 7) = 8 · 6 = 48
9 ∙ (14 – 6) = 9 · 8 = 72
7 · (12 – 3) = 7 · 9 = 63
Номер 5.
1) Маме 32 года, а сыну 8 лет. Во сколько раз мама старше сына? 2) Во сколько раз мама была старше сына 5 лет назад?
Ответ:
Задача 1:
1) 32 : 8 = 4 (раза)
Ответ: мама старше сына в 4 раза.
Задача 2:
1) 32 − 5 = 27 (л.)
2) 8 − 5 = 3 (г.)
3) 27 : 3 = 9 (р.)
Ответ: в 9 раз мама была старше сына.
1) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
Оформляем условие в виде краткой записи.
-(2023).jpg)
Рассуждаем.
Маме 32 года, а сыну – 8 лет. Чтобы узнать, во сколько одно число больше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз мама старше сына, нужно возраст мамы разделить на возраст сына.
32 : 8 = 4 (раза) – во столько раз мама старше сына.
Записываем ответ.
Ответ: мама старше сына в 4 раза.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
Нужно сравнить, во сколько раз мама была старше сына 5 лет назад. Но нам неизвестно, сколько лет было маме и сыну 5 лет назад. 5 лет назад им было на 5 лет меньше, поэтому, чтобы узнать, сколько лет было маме и сыну 5 лет назад, нужно из их возраста сейчас вычесть 5 лет.
32 − 5 = 27 (лет) − было маме 5 лет тому назад;
8 − 5 = 3 (года) − было сыну 5 лет тому назад;
Продолжаем рассуждение.
Мы узнали, что 5 лет назад маме было 27 лет, а сыну – 3 года. Чтобы узнать, во сколько одно число больше другого, нужно большее число разделить на меньшее. Значит, чтобы узнать, во сколько раз мама старше сына, нужно возраст мамы разделить на возраст сына.
27 : 3 = 9 (раз) − во сколько раз мама была старше сына 5 лет тому назад.
Записываем ответ.
Ответ: в 9 раз мама была старше сына.
Номер 6.
По таблице на обороте обложки учебника:
- найди произведение: 6 · 7, 4 · 8, 9 · 3, 4 · 9;
- проверь, что 7 · 8 = 8 · 7, 3 · 6 = 6 · 3;
- найди частное: 54 : 9, 32 : 4, 42 : 6, 35 : 5;
- назови числа от 6 до 60, которые делятся на 6;
- назови числа от 4 до 40, которые делятся на 4.
1) 6 · 7 = 42
4 · 8 = 32
9 · 3 = 27
4 · 9 = 36
2) 7 · 8 = 8 · 7 3 · 6 = 6 · 3
56 = 56 18 = 18
3) 54 : 9 = 6
35 : 5 = 7
32 : 4 = 8
42 : 6 = 7
4) 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
5) 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
Для выполнения задания обращайся к таблице умножения и деления чисел от 1 до 9.
Найдём произведение.
Произведение, значит, нужно найти числа, стоящие на пересечении 6 и 7, 4 и 8, 9 и 3, 4 и 9.
6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
4 · 8 = 32, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
9 · 3 = 27, где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
4 · 9 = 36, где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Проверим выражения.
Помни о существующем переместительном свойстве умножения.
Сравним 7 · 8 и 8 · 7.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
56 = 56, значит, 7 · 8 = 8 · 7
По переместительному свойству умножения.
Сравним 3 · 6 и 6 · 3.
3 · 6 = 18,
где 3 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
6 · 3 = 18,
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
18 = 18, значит, 3 · 6 = 6 · 3
По переместительному свойству умножения.
Найдём частное.
Частное – результат деления.
54 : 9 = 6, так как 9 · 6 = 45, где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
32 : 4 = 8, так как 4 · 8= 32, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
42 : 6 = 7, так как 6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
35 : 5 = 7, так как 5 · 7 = 35, где 5 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Рассуждаем.
Делятся на 6, значит, являются результатом таблицы умножения и деления 7.
-(2023).jpg)
Значит, выписываю числа: 6, 12, 18, 24, 30, 36, 42, 48, 54.
Рассуждаем.
Делятся на 4, значит, являются результатом таблицы умножения и деления 9.
-(2023).jpg)
Значит, выписываю числа: 4, 8, 12, 16, 20, 24, 28, 32, 36.
Оформляем задание в тетрадь.
Задание 1.
6 ∙ 7 = 42
4 ∙ 8 = 32
9 ∙ 3 = 27
4 ∙ 9 = 36
Задание 2.
7 ∙ 8 = 8 ∙ 7
По переместительному свойству умножения.
3 ∙ 6 = 6 ∙ 3
По переместительному свойству умножения.
Здание 3.
54 : 9 = 6
32 : 4 = 8
42 : 6 = 7
35 : 5 = 7
Задание 4.
Числа от 6 до 60, которые делятся на 6:
6, 12, 18, 24, 30, 36, 42, 48, 54, 60.
Задание 5.
Числа от 4 до 40, которые делятся на 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
Номер 7.
1) Начерти на листе клетчатой бумаги такой квадрат, вырежи его и разрежь по показанным на чертеже линиям. 2) Запиши номера фигур, которые ты сможешь выложить, используя полученные части квадрата. 3) Чему равна площадь каждой из этих фигур? 4) Верно ли, что все фигуры 1-5 будут симметричными?


1) Чертим квадрат, вырезаем его и разрезаем по показанным на чертеже линиям
2) 1, 3, 5.
3) Площадь фигуры 1 равна 9 см2.
Площадь фигуры 3 равна 9 см2
Площадь фигуры 5 равна 9 см2.
4) Да, верно, все фигуры симметричны:

1) Производи такие действия, составляй из частей фигуры, чтобы убедиться в верном решении этой задачи.
2) Чтобы вычислить площадь фигуры, нужно понять, сколько одинаковых квадратов помещается на плоскости.
3) Площадь фигуры измеряется в квадратных единицах.
Чертим и вырезаем.
Нужно начертить квадрат со стороной 3 см.
Потом полученный квадрат нужно вырезать и разрезать пополам по вертикали. А потом вторую половинку нужно полелить на два равных треугольника.
В итоге должно получиться три части: прямоугольник со сторонами 1 см 5 мм и 3 см и два треугольника.
-(2023).jpg)
Рассуждаем.
Рассмотрим фигуру 1. Данную фигуру можно составить из полученных частей. Два треугольника постваим по бокам прямоугольника.
-(2023).jpg)
Рассмотрм фигуру 2. Из полученных частей данную фигуру составить нельзя.
Рассмотрми фигуру 3. Данную фигуру можно составить из полученных частей. Два треугольника нужно расположить над прямоугольником.
-(2023).jpg)
Рассмотрим фигуру 4. Из полученных частей данную фигуру составить нельзя.
Рассмотрим фигуру 5. Данную фигуру можно составить из полученных частей. Два треугольника нужно разместить с правой сторны от прямоугольника.
-(2023).jpg)
Вычисляем площади фигур.
Площадь сложной фигуры складывается из площадей фигур, из которых она составлена.
Значит, чтбы узнать, какова площадь фигур 1, 3 и 5, нужно сначала вычислить площадь фигур, которые мы вычислили. Но полученные фигуры образуют квадрат со сторной 3 см.
Так как данные фигуры состоят из одинаковых фигур: прямоугольника и двух треугольников, значит и площади этих фигур одинаковы и равны площади данного квадрата.
3 ∙ 3 = 9 (см2) – площадь фигур 1, 3, 5.
Проверим симметрию.
Ось симметрии – линяя, по которой можно согнуть фигуру так, чтобы две половинки совпали, т.е. фигура разбилась пополам.
Все фигуры имеют ось симметрии, значит они симметричны.
-(2023).jpg)
Задание в низу страницы.
Найди по плану на с. 66 площадь огорода.

8 · 3 = 24 (м2) Ответ: площадь огорода равна 24 м2.
1) Площадь фигуры измеряется в квадратных единицах.
2) Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Рассмотрим рисунок.
.jpg)
На рисунке изображён план дачного участка. Нам нужно найти площадь огорода.
Чтобы это сделать найдём длину и ширину огорода на плане и на мместности.
Длина огорода на плане равна 8 клеток, так как 1 клетка на плане равна 1 м на местности, значит:
8 · 1 м = 9 м – длина огорода на местности.
Ширина огорода на плане равна 3 клетки, так как 1 клетка на плане равна 1 м на местности, значит:
3 · 1 м = 3 м – ширина огорода на метсности.
Найдём площадь огорода.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
8 ∙ 3 = 24 (м2) – площадь огорода на местности.
Записываем ответ.
Ответ: площадь огорода 24 м2.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.