Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 57

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
На рисунке изображены фигуры, которые при наложении не совпадут. Докажи, что их площади равны.

Все фигуры состоят из 4 квадратов одинаковой площади, значит площади фигур равны.
Фигуры называются равными, если они при наложении совпадают. Тогда их площади равны. В противном случае равны могут быть только площади, а при наложении фигуры не совпадут.
Рассмотрим фигуры.
Жёлтая фигура состоит из 4 одинаковых квадратов.
Зелёная фигура состоит из 4 одинаковых квадратов.
Розовая фигура состоит из 4 одинаковых квадратов.
Голубая фигура состоит из 4 одинаковых квадратов.
Сравним площади фигур.
Фигуры не равные, так как не совпадут при наложении. Но они имеют одинаковое количество квадратов, поэтому их площади равны.
Номер 2.
Ответ:7 ∙ 8 = 56 49 : 7 = 7 6 ∙ 7 = 42 63 : 9 = 7 7 ∙ 5 = 35 42 : 6 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7.
Выполняем умножение.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
7 · 5 = 35,
где 7 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Выполняем деление.
49 : 7 = 7,
так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
63 : 9 = 7,
так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
42 : 6 = 7,
так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
1 2
6 · 5 − 12 = 18
1) 6 · 5 = 30
2) 30 – 12 = (10 + 20) – 12 = 10 + (20 – 12) = 10 + 8 = 18
2 1
52 – 3 · 9 = 25
1) 3 · 9 = 27
2) 52 – 27 = 52 – (22 + 5) = (52 – 22) – 5 = 30 – 5 = 25
1 2
8 · 4 – 15 = 17
1) 8 · 4 = 4 · 8 = 32
2) 32 – 15 = 32 – (12 + 3) = (32 – 12) – 3 = 20 – 3 = 17
2 1
45 : (18 – 13) = 9
1) 18 – 13 = 5
2) 45 : 5 = 9
1 2
(27 + 27) : 9 = 6
1) 27 + 27 = 27 + (3 + 24) = (27 + 3) + 24 = 30 + 24 = 54
2) 54 : 9 = 6
2 1
24 : (11 – 7) = 6
1) 11 – 7 = 11 – (1 + 6) = (10 – 1) – 6 = 10 – 6 = 4
2) 24 : 4 = 6
Оформляем задание в тетрадь.
7 ∙ 8 = 56
6 ∙ 7 = 42
7 ∙ 5 = 35
49 : 7 = 7
63 : 9 = 7
42 : 6 = 7
6 ∙ 5 − 12 = 30 – 12 = 18
52 − 3 ∙ 9 = 52 – 27 = 25
8 ∙ 4 − 15 = 32 – 15 = 17
45 : (18 − 13) = 45 : 5 = 9
(27 + 27) : 9 = 54 : 9 = 6
24 : (11 − 7) = 24 : 4 = 6
Номер 3.
1) Запиши только те числа от 7 до 63, которые делятся на 7 без остатка.
2) Запиши все числа от 24 до 42. Подчеркни те, которые делятся на 6 без остатка.
1) 7, 14, 21, 28, 35, 42, 49, 56, 63. 2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
1) делятся на 7 без остатка, то есть являются результатами таблицы умножения семи.
2) делятся на 6 без остатка, то есть являются результатами таблицы умножения шести.
Вспомним таблицу умножения на 7.
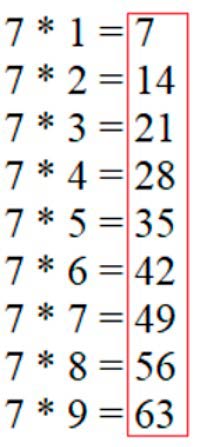
Выпишем числа.
Результат умножения на 7 и есть те числа, которые без остатка делятся на 7:
7, 14, 21, 28, 35, 42, 49, 56, 63.
Выпишем все числа от 24 до 42.
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Рассуждаем.
Вспомним таблиц умножения на 6.
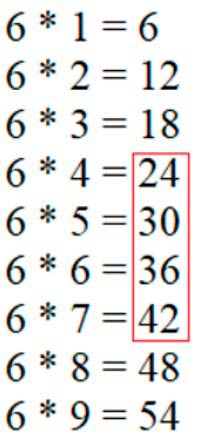
Результат умножения на 6 и есть те числа, которые без остатка делятся на 6.
Подчеркнем числа, которые делятся без остатка на 6:
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Оформим задание в тетрадь.
1) 7, 14, 21, 28, 35, 42, 49, 56, 63 – числа которые делятся без остатка на 7.
2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Номер 4.
От доски длиной 8 м отпилили часть длиной 2 м. Во сколько раз больше оставшаяся часть доски, чем отпиленная?
Ответ:

1-й способ решения:
1) 8 − 2 = 6 (м) осталось после отпила.
2) 6 : 2 = 3 (раз)
Ответ: в 3 раза оставшаяся часть доски больше, чем отпиленная.
2-й способ решения: (8 – 2) : 3 = 6 : 2 = 3 (раз) – больше во столько раз. Ответ: в 3 раза.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
Оформляем условие в виде краткой записи.
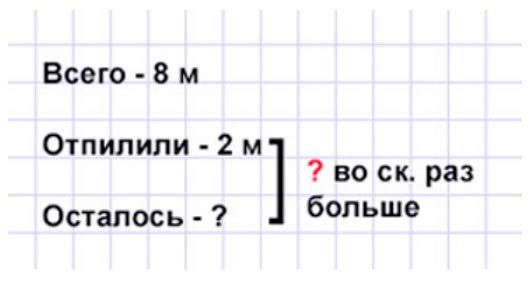
Рассуждаем.
Общая длина доски складывается из отрезанной части и оставшейся. Значит, чтобы узнать, сколько метров доски осталось, нужно из длины доски вычесть длину отрезанной части.
8 − 2 = 6 (м) осталось после отпила.
Продолжаю рассуждение.
Длина оставшейся части – 6 метров, а отрезанной – 2 метра. Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Значит, нужно длину оставшейся части разделить на длину отрезанной.
6 : 2 = 3 (раз) – во сколько раз больше оставшаяся часть доски, чем отпиленная.
Записываем ответ.
Ответ: в 3 раза больше оставшаяся часть доски больше, чем отпиленная.
Решение выражением: (8 – 2) : 2 = 3 (раза).
Номер 5.
Реши уравнения, подбирая значения х.
Ответ:
х · 7 = 42
х = 42 : 7
х = 6
Проверка:
6 · 7 = 42
42 = 42
Ответ: х = 6
36 : х = 4
х = 36 : 4
х = 9
Проверка:
36 : 9 = 4
4 = 4
Ответ: х = 9
9 · х = 45
х = 45 : 9
х = 5
Проверка:
9 · 5 = 45
45 = 45
Ответ: х = 5
х : 6 = 6
х = 6 · 6
х = 36
Проверка:
36 : 6 = 6
6 = 6
Ответ: х = 36
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия деления и умножения.
Рассмотрим уравнения.
х · 7 = 42,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
36 : х = 4,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
9 · х = 45,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х : 6 = 6,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Найдём значение уравнения.
х ∙ 7 = 42
Вспомни таблицу умножения на 7. На сколько нужно умножить число 7, чтобы получилось 42. Это число 6, так как 6 · 7 = 42.
х = 6
36 : х = 4
Вспомни таблицу умножения на 4. На сколько нужно разделить число 36, чтобы стало 4. Это число 9, так как 4 · 9 = 36.
х = 9
9 ∙ х = 45
Вспомни таблицу умножения на 9. На сколько нужно умножить число 9, чтобы получилось 45. Это число 5, так как 5 · 9 = 45.
х = 5
х : 6 = 6
Вспомни таблицу умножения на 6. Какое число нужно разделить на 6, чтобы получилось 6. Это число 36, так как 6 · 6 = 36.
х = 36
Делаем проверку.
х ∙ 7 = 42
Проверка: вместо х подставим число 6.
6 · 7 = 42
42 = 42 – верно.
36 : х = 4
Проверка: вместо х подставим число 9.
36 : 9 = 4, так как 4 · 9 = 36
4 = 4 – верно.
9 ∙ х = 45
Проверка: вместо х подставим число 5.
9 · 5 = 5 · 9 = 45
45 = 45 – верно.
х : 6 = 6
Проверка6 вместо х подставим число 36.
36 : 6 = 6, так как 6 · 6 = 36
6 = 6 – верно.
Оформляем задание в тетрадь.
х ∙ 7 = 42
х = 6
Так как 6 · 7 = 42
36 : х = 4
х = 9
Так как 4 · 9 = 36
9 ∙ х = 45
х = 5
Так как 5 · 9 = 45
х : 6 = 6
х = 36
Так как 6 · 6 = 36
Задание внизу страницы
Узнай, площадь какой фигуры больше.

Нужно сосчитать количество клеточек, из которых состоит каждая фигура.
Зелёная фигура 42 клетки.
Красная фигура 48 клеток.
42 < 48
Ответ: площадь второй фигуры больше.
1) Площадь фигуры – часть плоскости, на которой она лежит.
2) Чтобы узнать площадь фигуры, нужно посмотреть, из скольких одинаковых клеток она составлена.
Рассуждаем.
Чтобы определить площадь фигуры можно посчитать количество клеток.
В зелёной фигуре 42 клетки, значит и площадь равна 42.
Красная фигура - 48 клеток, значит площадь равна 48.
Продолжаем рассуждение.
Также площадь фигуры можно вычислить если разбить её на участки.
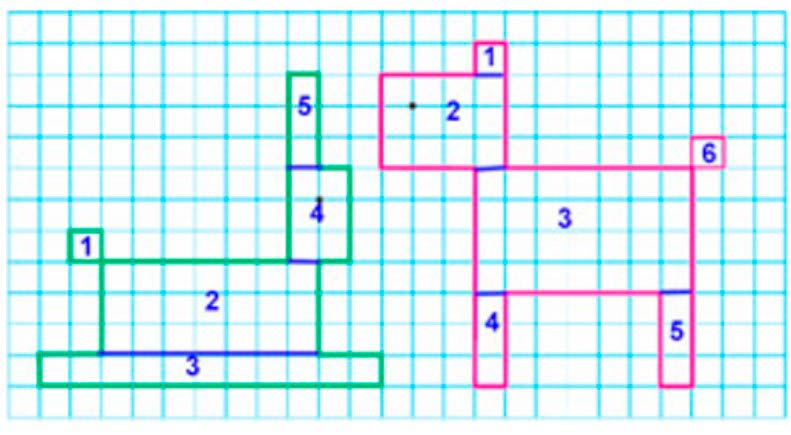
Зеленая фигура:
1 – 1 клетка.
2 – 3 строчки по 7 клеток – 3 ∙ 7 = 21 клетка.
3 – 11 клеток.
4 – 3 строчки по 2 клетки – 3 ∙ 2 = 6 клеток.
5 – 3 клетки.
Всего: 1 + 21 + 11 + 6 + 3 = 22 + 20 = 42 клетки – в зеленой фигуре.
Красная фигура:
1 – 1 клетка.
2 – 3 строчки по 4 клетки – 3 ∙ 4 = 12 клеток.
3 – 4 строчки по 7 клеток – 4 ∙ 7 = 28 клеток.
4 – 3 клетки.
5 – 3 клетки.
6 – 1 клетка.
Всего: 1 + 12 + 28 + 3 + 3 + 1 = 13 + 31 + 4 = 44 + 4 = 48 клеток.
Сравним фигуры.
42 клетки < 48 клеток, значит площадь зеленой фигуры меньше, чем красной фигуры.
Ответ: площадь красной фигуры больше.
Задание на полях страницы
Какой предмет лишний?

Ответ:
Лишняя линейка. Она плоская. Лишний мяч. У него нет углов.
Чтобы узнать, какой предмет лишний, рассмотри все. Какие признаки они имеют: цвет, размер, форма, отношение к пространству.
Рассмотрим предметы.
Предмет 1 – красный куб – объемная фигура.
Предмет 2 – оранжевый мяч – объемная фигура.
Предмет 3 – плоский угольник – плоский предмет.
Предмет 4 – коробка – объемная фигура.
Делаем вывод.
Угольник лишний предмет, так как это плоская фигу, а остальные объемные.
Номер 3.
1) Вычисли площадь прямоугольника, длины сторон которого 9 см и 2 см.
2) Какими ещё могут быть длины сторон прямоугольника с такой площадью?
1) а = 9 см
b = 2 см
S = ? см2
S = a ∙ b
S = 9 ∙ 2 = 18 см2.
2) 6 см и 3 см
1 см и 18 см
1) Площадь фигуры измеряется в квадратных сантиметрах (см2).
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
Оформляем условие в виде краткой записи.
.jpg)
Длина – 9 см
Ширина – 2 см
Площадь – ?
Рассуждаем.
У прямоугольника длина равна – 9 см, а ширина – 2 см. Значит для того чтобы вычислить площадь прямоугольника умножим длину на ширину.
9 · 2 = 18 (см2) – площадь прямоугольника.
Продолжаем рассуждение.
Чтобы понять какими могут быть другие пары сторон, нужно подобрать такие числа – множители, которые при произведении образуют число 18.
Это числа 3 и 6, 1 и 18, так как 3 · 6 = 18 и 1 · 18 = 18.
Значит стороны могут быть равны 3 см и 6 см, 1 см и 18 см.
Записываем ответ.
Ответ: площадь прямоугольника – 18 2, при этом сторны могут быть равны 3 см и 6 см или 1 см и 18 см.
Номер 4.
Начерти два квадрата: один со стороной 2 см, другой со стороной 3 см. Разбей каждый квадрат со стороной 3 см. Разбей каждый квадрат на квадратные сантиметры и найди его площадь.
Ответ:
1) 3 ∙ 3 = 9 см2
2) 2 ∙ 2 = 4 см2
1) Чтобы вычислить площадь фигуры, нужно понять, сколько одинаковых квадратов помещается на плоскости.
2) Площадь фигуры измеряется в квадратных сантиметрах (см2).
3) Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
Начертим первый квадрат.
Начертим квадрат со стороной 2 см и разобьем его на квадратные сантиметры – это значит разбить на квадратики со стороной 1 см.
-(2023).jpg)
Рассуждаем.
Квадрат со стороной 2 см состоит из 4 квадратов площадью 1 см2.
Значит, во всём прямоугольнике уложится 4 квадрата площадью 1 см2.
В итоге, площадь прямоугольника 4 см2.
Также площадь можно найти умножив длину на ширину. У квадрата все стороны равны. Значит, сторону квадрата умножим два раза.
2 · 2 = 4 (см2) – площадь квадрата со сторной 2 см.
Записываем ответ.
Ответ: площадь квадрата со стороной 2 см равна 4 см2.
Начертим второй квадрат.
Начертим квадрат со стороной 3 см и разобьем его на квадратные сантиметры – это значит разбить на квадратики со стороной 1 см.
-(2023).jpg)
Рассуждаем.
Квадрат со стороной 3 см состоит из 9 квадратов площадью 1 см2.
Значит, во всём прямоугольнике уложится 9 квадрата площадью 1 см2.
В итоге, площадь прямоугольника 9 см2.
Также площадь можно найти умножив длину на ширину. У квадрата все стороны равны. Значит, сторону квадрата умножим два раза.
3 · 3 = 9 (см2) – площадь квадрата со сторной см.
Записываем ответ.
Ответ: площадь квадрата со стороной 3 см равна 9 см2.
Номер 5.
56 : 7 2 · 6 : 4
54 : 9 2 · 3 : 6
36 : 4 1 · 9 : 3
36 : (11 - 2) · 7
42 : (14 - 7) · 9
48 : (12 - 6) · 4
50 - 27 : 3
34 + 9 · 4
40 - 54 : 6
56 : 7 = 8
54 : 9 = 6
36 : 4 = 9
2 · 6 : 4 = 12 : 4 = 3
2 · 3 : 6 = 6 : 6 = 1
1 · 9 : 3 = 9 : 3 = 3

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7.
Выполняем деление.
56 : 7 = 8, так как 7 · 8 = 56, где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
54 : 9 = 6, так как 6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
36 : 4 = 9, так как 4 · 9 = 36, где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
Расставляем порядок действий и выполняем вычисления.
1 2
2 · 6 : 4 = 3
1) 2 · 6 = 12
2) 12 : 4 = 3, так как 3 · 4 = 12
1 2
2 · 3 : 6 = 1
1) 2 · 3 = 6
2) 6 : 6 = 1
Если число разделить на само себя, то получится 1.
1 2
1 · 9 : 3 = 3
1) 1 · 9 = 9
Если число умножить на 1, то число не изменится.
2) 9 : 3 = 3, так как 3 · 3 = 9
2 1 3
36 : (11 − 2) · 7 = 28
1) 11 – 2 = 11 – (1 + 1) = (11 – 1) – 1 = 10 – 1 = 9
Представим число 2 в виде суммы чисел 1 и 1. Сначала из числа 11 вычтем число 1, а потом ещё раз вычтем число 1.
2) 36 : 9 = 4, так как 4 · 9 = 36
3) 4 · 7 = 28
2 1 3
42 : (14 – 7) · 9 = 54
1) 14 – 7 = 14 – (4 + 3) = (10 – 4) – 3 = 10 – 3 = 7
Представим число 7 в виде суммы числе 4 и 3. Сначала из числа 14 вычтем число 4, а потом вычтем число 3.
2) 42 : 7 = 6, так как 6 · 7 = 42
3) 6 · 9 = 54
2 1 3
48 : (12 – 6) · 4 = 32
1) 12 – 6 = 12 – (2 + 4) = (12 – 20 – 4 = 10 – 4 = 6
Представим число 6 в виде суммы чисел 2 и 4. Вначале из числа 12 вычтем число 2, а потом вычтем число 4.
2) 48 : 6 = 8, так как 6 · 8 = 48
3) 8 · 4 = 32
2 1
50 – 27 : 3 = 41
1) 27 : 3 = 9, так как 3 · 9 = 27
2) 50 – 9 = 41
2 1
34 + 9 · 4 = 70
1) 9 · 4 = 4 · 9 = 36
2) 34 + 36 = (30 + 30) + (3 + 6) = 60 + 10 = 70
Десятки сложим с десятками, а единицы сложим с единицами.
2 1
40 – 54 : 6 = 31
1) 54 : 6 = 9, так как 6 · 9 = 54
2) 40 – 9 = (30 + 10) – 9 = 30 + (10 – 9) = 30 + 1 = 31
Представим число 40 в виде суммы чисел 30 и 10. Вначале из числа 10 вычтем число 9, а потом к полученному результату прибавим число 30.
Оформляем задание в тетрадь.
56 : 7 = 8
54 : 9 = 6
36 : 4 = 9
2 ∙ 6 : 4 = 12 : 4 = 3
2 ∙ 3 : 6 = 6 : 6 = 1
1 ∙ 9 : 3 = 9 : 3 = 3
36 : (11 − 2) ∙ 7 = 36 : 9 · 7 = 4 · 7 = 28
42 : (14 − 7) ∙ 9 = 42 : 7 · 9 = 6 · 9 = 54
48 : (12 − 6) ∙ 4 = 48 : 6 · 4 = 8 · 4 = 32
50 − 27 : 3 = 50 – 9 = 41
34 + 9 ∙ 4 = 34 + 36 = 70
40 − 54 : 6 = 40 – 9 = 31
Номер 6.
В 4 банки поровну разлили 20 кг мёда. Хватит ли 7 банок, чтобы так же разлить 37 кг мёда? Если нет, то определи, сколько килограммов мёда останется.
Ответ:
1) 20 : 4 = 5 (кг) – меда в одной банке.
2) 5 · 7 = 35 (кг.) – в 7 банках
3) 37 - 35 = 2 (кг) – останется
Ответ: семи банок не хватит, потому что останется 2 кг мёда.
Данная задача: вида «вместимость 1 банки, количество банок, общая масса меда» характеризуется зависимостями между компонентами:
Вместимость 1 банки · количество банок = общая масса меда.
Общая масса меда : количество банок = вместимость 1 банки.
Общая масса меда : вместимость 1 банки = количество банок.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Узнаем, сколько меда помещается в одну банку, для этого общее количество меда разделим на количество банок, в которые он был разлит.
1) 20 : 4 = 5 (кг) – меда в одной банке.
Продолжаем рассуждение.
Вычислим, сколько кг меда будет в семи банках, для этого количество меда в одной банке нужно умножить на количество банок.
2) 5 · 7 = 35 (кг) – в 7 банках.
Продолжаем рассуждение.
37 кг меда в 7 банок не поместятся, такой вывод мы можем сделать, исходя из второго действия. Узнаем, сколько кг меда останется.
3) 37 − 35 = 2 (кг) – останется.
Записываем ответ.
Ответ: останется 2 кг.
Номер 7.
Из 24 м ситца сшили 8 одинаковых халатов. Сколько таких халатов можно сшить из 15 м ситца?
Ответ:
1) 24 : 8 = 3 (м) – на один халат.
2) 15 : 3 = 5 (х.)
Ответ: 5 халатов можно сшить из 15 метров ситца.
Данная задача: вида «расход на 1 халат, количество халатов, общее количество ткани» характеризуется зависимостями между компонентами:
Расход на 1 халат · количество халатов = общее количество ткани.
Общее количество ткани : количество халатов = расход на 1 халат.
Общее количество ткани : расход на 1 халат = количество халатов.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
На 8 одинаковых халатов израсходовали 24 метра ткани. Значит, нам известно количество халатов и общее количество ткани, но неизвестен расход на 1 халат. При это он одинаковый. Значит, чтобы узнать, каков расход ткани на 1 халат, нужно общее количество ткани разделить на количество халатов.
24 : 8 = 3 (м) – потребуется на один халат.
Продолжаем рассуждение.
Мы узнали, что расход на 1 халат – 3 метра и он одинаковый. Также нам известно общее количество ткани, которую расходовали на все халаты. Значит, чтобы узнать, сколько халатов сшили из всей ткани, нужно разделить общее количество ткани на расход на 1 халат.
15 : 3 = 5 (х.) – можно сшить из 15 м.
Записываем ответ.
Ответ: можно сшить 5 халатов.
Решение выражением:
15 : (24 : 8) = 5 (х.), где 24 : 8 – расход ткани на 1 халат.
Номер 8.
Составь различные верные равенства с числами 68, 12, 56.
Ответ:68 - 12 = 56
68 - 56 = 12
56 + 12 = 68
12 + 56 = 68
1) Помни о названии компонентов действия сложения и зависимости между компонентами и результатом действия сложения.
2) Переместительное свойство умножения – от перестановки мест множителей, значение произведения не изменяется, т.е. а · b = b · а.
Составим различные суммы из чисел 68, 12, 56.
68 + 12 = (60 + 10) + (8 + 2) = 70 = 10 = 80 – не подходит, так как числа 80 в данном ряду нет.
68 + 56 = 68 + (2 + 54) = (68 + 2) + 54 = 70 + 54 = 124 – не подходит, так как числа 124 в данном ряду нет.
12 + 56 = (10 + 50) + (2 + 6) = 60 + 8 = 68 – подходит.
56 + 12 = 68 – подходит.
Составим разности из чисел 68, 12, 56.
Из большего числа вычтем меньшее число.
68 – 12 = (60 – 10) + (8 – 2) = 50 + 6 = 56 – подходит.
68 – 56 = (60 – 50) + (8 – 6) = 10 + 2 = 12 – подходит.
Оформим задание в тетрадь.
56 + 12 = 68
12 + 56 = 68
68 − 12 = 56
68 − 56 = 12
Номер 9.
Аня, Денис и Коля начертили по одной фигуре: Аня и Денис начертили фигуры с одинаковым числом сторон, а Коля и Денис начертили фигуры с одинаковым периметром. Кто какую фигуру начертил?
1) Сравни периметры двух четырёхугольников.
2) Сколько осей симметрии у фигуры: 1? 2? 3?

Денис начертил квадрат;
Аня начертила четырёхугольник;
Коля начертил треугольник.
1) Периметр красного квадрата:
2 ∙ 4 = 8 (см)
Периметр синего четырёхугольника:
2 + 2 + 1 + 1 = 6 (см)
Периметр зелёного треугольника:
3 + 3 + 2 = 8 (см)
Периметр красного квадрата на 2 см больше, чем периметр синего четырехугольника.
2) В 1 фигуре 4 оси симметрии.

Во 2 и 3 фигурах по 1 оси симметрии

1) Помни, что фигуры называют по количеству углов.
2) Ось симметрии – линия, по которой можно сложить фигуру так, что части совпадут при перегибании, т.е. наложении.
3) Помним, что периметр – это сумма длин всех сторон. Значит нужно сложить все стороны.
Рассмотрим фигуры.
-(2023).jpg)
Фигура 1 – квадрат имеет 4 стороны.
Фигура 2 – четырехугольник имеет 4 стороны.
Фигура 3 – треугольник имеет 3 угла.
Рассуждаем.
Так как фигура 1 и фигура 2 имеют одинаковое количество сторон, то первую и вторую фигуры начертили Аня и Денис, а третью фигуру начертил Коля.
Найдём периметры фигур.
Чтобы узнать какую фигуру начертили Аня и Денис нужно найти периметры этих фигур.
Измерим стороны фигур с помощью линейки:
Фигура 1 – имеет 4 одинаковые стороны по 2 см.
Фигура 2 – состоит из сторон 2 см, 2 см, 1 см, 1 см.
Фигура 3 – состоит из трёх сторон 3 см, 3 см, 2 см.
Найдём периметры фигур.
1) Квадрат:
Так как все стороны равны, то сложение одинаковых слагаемых можно заменить умножением. Значит, длину стороны умножаем на количество сторон.
2 · 4 = 8 (см) – периметр фигуры 1.
2) Четырехугольник:
Сложим длины сторон.
2 + 2 + 1 + 1 = 4 + 2 = 6 (см) – периметр фигуры 2.
3) Треугольник:
Сложим длины сторон.
3 + 3 + 2 = 6 + 2 = 8 (см) – периметр треугольника.
Продолжим рассуждение.
Коля и Денис начертили фигуры с одинаковыми периметрами, а у квадрата и треугольника периметры равны. Но при этом Аня и Денис начертили квадрат и четырехугольник. Поэтому:
Денис начертил четырёхугольник,
Аня – квадрат,
Коля – треугольник.
Сравним периметры четырехугольников.
8 см > 6 см – периметр квадрата больше периметра четырехугольника.
Чтобы узнать на сколько один периметр больше другого, нужно из большего периметра вычесть меньший периметр. Значит из значения периметра квадрата вычтем значение периметра четырехугольника.
8 – 6 = 2 (см) — периметр квадрата больше на 2 см.
Рассмотрим фигуры и оси симметрии.
У квадрата 4 оси симметрии – горизонтальная, вертикальная и две диагональные оси симметрии.
-(2023).jpg)
У четырехугольника и треугольника по 1 оси симметрии.
-(2023).jpg)
Запишем ответ.
Ответ: Денис - четырёхугольник, Аня – квадрат, Коля – треугольник.
1) периметр квадрата на 2 см больше, чем периметр четырехугольника.
2) фигура 1 – 4 оси симметрии; фигура 2 – 1 ось симметрии; фигура 3 – 1 ось симметрии.
Задание внизу страницы.
Вычисли площадь прямоугольника со сторонами 5 см и 6 см.
Ответ:a = 5 см
b = 6 см
S = ? см2
S = a ∙ b
S = 5 ∙ 6
S = 30 см2
Ответ: Площадь прямоугольника равна 30 см2.
1) Площадь фигуры измеряется в квадратных сантиметрах (см2).
2) Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Оформляем условие в виде краткой записи.
-(2023).jpg)
Длина – 6 см
Ширина – 5 см
Площадь – ?
Найдём площадь прямоугольника.
У прямоугольника длина равна – 6 см, а ширина – 5 см. Значит для того чтобы вычислить площадь прямоугольника умножим длину на ширину. 6 · 5 = 30 (см2) – площадь прямоугольника.
Записываем ответ.
Ответ: площадь прямоугольника 30 см2.
Задание не полях страницы.
Найди лишнее выражение:
48 : 8
36 : 6
60 : 10
54 : 9
42 : 7
56 : 7
30 : 5
48 : 8 = 6
36 : 6 = 6
60 : 10 = 6
54 : 9 = 6
42 : 7 = 6
30 : 5 = 6
56 : 7 = 8 – лишнее выражение.
Пояснение: выражение 56 : 7 лишнее, потому что его значение отличается от других и равно 8.
Чтобы понять, какое выражение лишнее, нужно сравнить все: из каких компонентов составлены, на каких арифметических действиях основаны, каково их значение.
Вычислим значения всех выражений, чтобы понять, чем они похожи, а чем отличаются.
48 : 8 = 6,
так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
36 : 6 = 6,
так как 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
60 : 10 = 6,
так как 6 · 10 = 60,
где 6 – одинаковое слагаемое, а 10 – количество одинаковых слагаемых.
54 : 9 = 6,
так как 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
42 : 7 = 6, так как 7 · 6 = 42,
где 7 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
56 : 7 = 8,
так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
30 : 5 = 6,
так как 5 · 6 = 30,
где 5 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Сделаем вывод.
Все выражения основаны на действии деления, значение всех выражений равно 6, а у одного выражения – 8.
Значит, лишнее выражение – 56 : 7.
Запишем ответ.
Ответ: выражение 56 : 7 = 8 – лишнее.
Назови фигуры:

куб, пятиугольник, шар
Вспомним названия геометрических фигур.
Рассмотрим фигуры на полях страницы.
-(2023).jpg)
Назовем каждую из них.
Куб, пятиугольник, шар.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.