Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 5

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Вычисли, переставляя, где удобно, слагаемые или заменяя соседние слагаемые их суммой.
Ответ:
65 + 9 + 5 = (65 + 5) + 9 = 79
76 + 8 + 4 = (76 + 4) + 8 = 88
36 + 8 + 12 = (8 + 12) + 36 = 20 + 36 = 56
47 + 6 + 24 = (6 + 24) + 47 = 30 + 47 = 77
20 + 27 + 3 + 30 = (27 + 3) + (20 + 30) = 30 + 50 = 80
50 + 19 + 1 + 20 = (19 + 1) + (50 + 20) = 20 + 70 = 90
Используются следующие свойства арифметических действий:
a + b = b + a – переместительное свойство сложения
(a + b) + c = a + (b + c) - сочетательное свойство сложения
Выполним устные рассуждения.
65 + 9 + 5 = (65 + 5) + 9 = 70 = 9 = 79
Сначала сложим числа 65 и 5, а после к полученной сумме прибавим 9.
76 + 8 + 4 = (76 + 4) + 8 = 80 + 8 = 88
Сначала сложим числа 76 и 4, а после к полученной сумме прибавим 8.
36 + 8 + 12 = (8 + 12) + 36 = 20 + 36 = 56
Сначала сложим числа 8 и 12, а после к полученной сумме прибавим 36.
47 + 6 + 24 = (6 + 24) + 47 = 30 + 47 = 77
Сначала сложим числа 6 и 24, а после к полученной сумме прибавим 47.
20 + 27 + 3 + 30 = (27 + 3) + (20 + 30) = 30 + 50 = 80
Поочередно складываем числа 27 с числом 3 и 20 с числом 30. После полученные результаты складываем.
50 + 19 + 1 + 20 = (19 + 1) + (50 + 20) = 20 + 70 = 90
Поочередно складываем числа 19 с числом 1 и 50 с числом 20. После полученные результаты складываем.
Оформим задание в тетрадь
65 + 9 + 5 = 70 + 9 = 79
76 + 8 + 4 = 80 + 8 = 88
36 + 8 + 12 = 20 + 36 = 56
47 + 6 + 24 = 30 + 47 = 77
20 + 27 + 3 + 30 = 30 + 50 = 80
50 + 19 + 1 + 20 = 20 + 70 = 90
Номер 2.
Реши с устным объяснением.
Ответ:
Помним, что складывать можно только единицы с единицами, а десятки с десятками. Вычитать тоже можно только единицы из единиц и десятки из десятков.
Помни, что 1 дес. = 10 ед.
Выполним устные рассуждения.
43 + 12 = 55
Складываем единицы. 3 + 2 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Складываем десятки. 4 + 1 = 5 – получилось десятков.
Записываем в разряде десятков число 5.
Читаем ответ: 55.
57 + 23 = 80
Складываем единицы. 7 + 3 = 10 – получилось 1 дес. и 0 ед.
Записываем в разряде единиц число 0, а 1 дес. запоминаем.
Складываем десятки. 5 + 2 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десятков.
Записываем в разряде десятков число 8.
Читаем ответ: 80.
24 + 67 = 91
Складываем единицы. 4 + 7 = 11 – получилось 1 дес. и 1 ед.
Записываем в разряде единиц число 1, а 1 дес. запоминаем.
Складываем десятки. 2 + 6 = 8 и ещё 1 дес., который запомнили 8 + 1 = 9 – получилось десяток.
Записываем в разряде десятков число 9.
Читаем ответ: 91.
35 – 21 = 14
Вычитаем единицы. 5 – 1 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. 3 – 2 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 14.
95 – 65 = 30
Вычитаем единицы. 5 – 5 = 0 – получилось единиц.
Записываем в разряде единиц число 0.
Вычитаем десятки. 9 – 6 = 3 – получилось десятков.
Записываем в разряде десятков число 3.
Читаем ответ: 30.
83 – 26 = 57
Вычитаем единицы. От числа 3 мы не можем отнять 6.
Занимаем 1 дес. = 10 ед., 10 + 3 = 13 ед., 13 – 6 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 8 дес., мы занимали 1 дес, осталось 8 – 1 = 7 дес.,
7 – 2 = 5 – получилось десятков.
Записываем в разряде десятков число 5.
Читаем ответ: 57.
Оформим задание в тетрадь
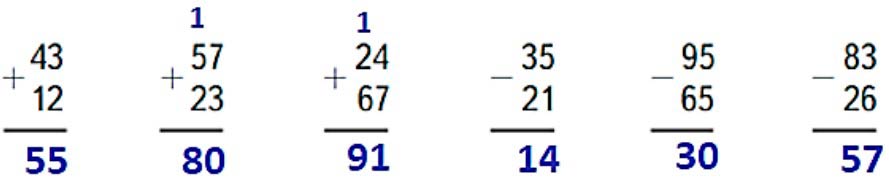
Номер 3.
Длина кита от хвоста до головы 16 м, а длина головы на 12 м меньше. Объясни, что узнаешь, выполнив вычисления: 16 − 12 16 + (16 − 12)
Ответ:16 − 12 = 4 (м) – длина головы кита. 16 + (16 − 12) = 20 (м) – длина всего кита.
Первое действие вычисляется вычитанием.
Второе действие вычисляется сложением.
Оформляем условие в виде краткой записи.

Рассуждаем.
Вычислим длину головы.
Длина головы кита на 12 м меньше, чем длина от хвоста от головы.
Значит, чтобы найти длину головы нужно из длины кита от хвоста до головы нужно вычесть 12 м.
16 – 12 = 4 (м) – длина головы
Продолжим рассуждения.
Найдём общую длину кита.
Общая длина кита складывается из длины от хвоста до головы и длины самой головы. Нужно сложить длину от хвоста до головы и головы.
16 + 4 = 20 (м) – длина кита
Запишем ответ.
Ответ: 20 м.
Решение выражением: 16 + (16 – 12) = 20 (м.), где 16 – 12 – длина головы.
Номер 4.
На каникулах Ваня был в спортивном лагере 3 недели, а в деревне у бабушки на 1 неделю больше, чем в лагере. Сколько всего недель Ваня был в спортивном лагере и в деревне?
Ответ:

1) 3 + 1 = 4 (н.) – Ваня был в деревне.
2) 3 + 4 = 7 (н.)
Ответ: 7 недель был в лагере и деревне.
Первое действие вычисляется сложением
Второе действие вычисляется сложением
Оформляем условие в виде краткой записи.

Рассуждаем.
Вычислим сколько недель Ваня пробыл в деревне.
Ваня был в спортивном лагере 3 недели, а в деревне на 1 неделю больше. Значит, столько же, и еще 1 неделя.
3 + 1 = 4 (нед.) – был в деревне у бабушки
Продолжим рассуждения.
Вычислим общее количество недель.
Общее количество недель, что Ваня провел не дома, складывается из количества недель, проведенных в лагере и у бабушки. Значит, нужно сложить время, проведенное в лагере и у бабушки.
3 + 4 = 7 (нед.) – был в лагере и в деревне
Записываем ответ.
Ответ: 7 недель.
Решение с помощью выражения: 3 + (3 + 1) = 7 (нед.), где 3 + 1 – количество недель, проведенных в лагере.
Номер 5.
Составь верные равенства и неравенства, используя следующие выражения:
Ответ:
Прежде, чем составлять равенства и неравенства, необходимо вычислить их значения.
Вычисление значений выражения сводится к применению правил:
(а + в) + с = (а + с) + в - прибавления числа к сумме;
а – (в + с) = (а – в) – с - вычитания суммы из числа;
(а + в) – с = (а – с) + в - вычитания числа из суммы.
Выполним устные рассуждения.
18 + 2 = (10 + 8) + 2 = 10 + (8 + 2) = 10 + 10 = 20,
Разложим число 18 на сумму чисел 10 и 8.
Используем правило прибавления числа к сумме.
34 – 14 = 34 – (10 + 4) = (34 – 4) – 10 = 30 – 10 = 20
Разложим число 14 на сумму чисел 10 и 4.
Используем правило вычитания суммы из числа.
56 – 50 = (50 + 6) – 50 = (50 – 50) + 6 = 0 + 6 = 6,
Разложим число 56 на сумму чисел 50 и 6.
Используем правило вычитания числа из суммы.
70 – 50 = 7 дес. – 5 дес. = 2 дес. = 20
Запишем равенства и неравенства в тетрадь.
Равенства: Неравенства:
18 + 2 = 34 – 14 34 − 14 > 56 − 50;
18 + 2 = 70 – 50 70 − 50 > 56 – 50;
34 − 14 = 70 – 50 18 + 2 > 56 – 50.
Номер 6.
Ответ:
1 см 6 мм = 16мм
16 мм = 16 мм
3 дм 8 см < 40 см
38 см < 40 см
8 дм > 79 см
80 см > 79 см
2 м 1 дм > 1 м 2 дм
21 дм > 12 дм
Помним, сравнивать можно только числовые значения, выраженные в одних единицах измерения:
Помни, что 1 см = 10 мм
1 дм = 10 см
1 м = 10 дм
Рассуждаем.
1 см 6 мм = 10 мм + 6 мм = 16 мм
3 дм 8 см < 40 см
3 дм 8 см = 30 см + 8 см = 38 см
38 см < 40 см
8 дм > 79 см
8 дм = 80 см
80 см > 79 см
2 м 1 дм > 1 м 2 дм
2 м 1 дм = 20 дм + 1 дм = 21 дм
Оформляем задание в тетрадь.
1 см 6 мм = 16 мм
3 дм 8 см < 40 см
8 дм > 79 см
2 м 1 дм > 1 м 2 дм
Номер 7.
Начерти ломаную из трех звеньев так, чтобы длина каждого звена была равна 6 см. Узнай длину ломаной.
Ответ:
6 + 6 + 6 = 18 (см) – длина ломаной. Ответ: 18 см общая длина ломаной.
Вспомним определения.
1) Ломаная линия – геометрическая фигура, состоящая из звеньев-отрезков, не лежащих на одной прямой.
2) Длина ломаной – сумма длин всех его отрезков.
Рассуждаем.
Чтобы вычислить длину ломаной, необходимо измерить длины всех звеньев, а полученные значения сложить.
У ломаной, по условию задачи, длины звеньев одинаковые. Значит, сложение одинаковых слагаемых можно заменить умножением.
6 + 6 + 6 = 6 · 3 = 18 см – длина ломанной
Чертим ломанную.
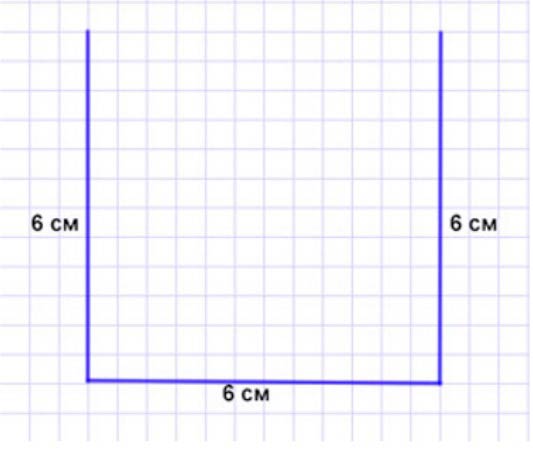
Записываем ответ.
Ответ: 18 см длина ломанной.
Номер 8.
Какие фигуры изображены на чертеже? На какие две группы их можно разбить? Найди разные способы.

Ответ:
На чертеже изображены: треугольники и четырехугольники.
Фигуры делятся на:
– розовые или синие фигуры;
– треугольники и четырехугольники.
Рассмотри фигуры. Попытайся найти разные основания для разбиения всех фигур на группы. Для это сначала охарактеризуй все изображенные фигуры.
Охарактеризуем каждую фигуру по цвету и количеству углов
1. Голубой треугольник
2. Голубой четырехугольник
3. Розовый четырехугольник
4. Голубой треугольник
5. Розовый треугольник
6. Голубой четырехугольник
7. Розовый четырехугольник
8. Голубой четырехугольник
9. Розовый четырехугольник
Продолжаем рассуждение.
Каждая фигура обладает двумя свойствами: цвет и количество углов, а именно эти свойства являются основаниями, для разбиения изображенных фигур на группы.
Разбиваем на группы.
1 группа – По цвету:
Голубой – 1, 2, 4, 6, 8
Розовый – 3, 5, 7, 9
2 группа – По количеству углов:
Треугольники – 1, 4, 5, 8
Четырехугольники – 2, 3, 6, 7, 9
Номер 9.
Красная лента короче синей, а синяя лента короче белой. Какая лента самая длинная?
Ответ:1-й способ решения: Самая длинная лента – белая.
2-й способ решения: Красная лента короче синей ленты, и она не может быть самой длинной. Синяя лента короче белой, и она не может быть самой длинной. Значит, самая длинная лента – белая.
Длиннее, значит, больше.
Короче, значит, меньше.
Рассуждаем.
Красная лента < Синей ленты
Синяя лента < белой ленты
Если мы объединим данные неравенства, то получим:
Красная < Синяя < Белая
Значит, самая длинная лента – белая.
Проиллюстрируем.
Рассмотрим сравнение с помощью рисунка.

Записываем ответ.
Ответ: белая лента самая длинная.
Задание внизу страницы
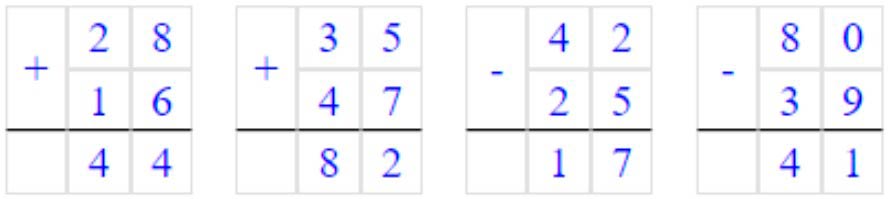
Вычисли, записывая решение столбиком.
Ответ:
Помним, что складывать можно только единицы с единицами, а десятки с десятками. Вычитать тоже можно только единицы из единиц и десятки из десятков.
Помни, что 1 дес. = 10 ед.
Устные рассуждения
28 + 16
Складываем единицы. 8 + 6 = 14 – получилось 1 дес. и 4 ед.
Записываем в разряде единиц число 4, а 1 дес. запоминаем.
Складываем десятки. 2 + 1 = 3 и ещё 1 дес., который запомнили 3 + 1 = 4 – получилось десяток.
Записываем в разряде десятков число 4.
Читаем ответ: 44.
35 + 47
Складываем единицы. 5 + 7 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. 3 + 4 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десяток.
Записываем в разряде десятков число 8.
Читаем ответ: 82.
42 – 25
Вычитаем единицы. От числа 2 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 + 2 = 12 ед., 12 – 5 = 7 – получилось единиц.
Записываем в разряде единиц число 7.
Вычитаем десятки. Было 4 дес., мы занимали 1 дес, осталось 4 – 1 = 3 дес.,
3 – 2 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 17.
80 – 39
Вычитаем единицы. От числа 0 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 + 0 = 10 ед., 10 – 9 = 1 – получилось единиц.
Записываем в разряде единиц число 1.
Вычитаем десятки. Было 8 дес., мы занимали 1 дес, осталось 8 – 1 = 7 дес.,
7 – 3 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 41.
Оформляем задание в тетрадь
Номер 1.
Вычисли.
Ответ:
65 + 9 + 5 = (65 + 5) + 9 = 79
76 + 8 + 4 = (76 + 4) + 8 = 88
36 + 8 + 12 = (8 + 12) + 36 = 20 + 36 = 56
47 + 6 + 24 = (6 + 24) + 47 = 30 + 47 = 77
20 + 27 + 3 + 30 = (27 + 3) + (20 + 30) = 30 + 50 = 80
50 + 19 + 1 + 20 = (19 + 1) + (50 + 20) = 20 + 70 = 90
Основные законы сложения:
1. Переместительный закон.
Сумма не меняется от перестановки её слагаемых: a + b = b + a.
2. Сочетательный закон.
Сумма не зависит от группировки её слагаемых: (a + b) + c = a + (b + c) = a + b + c.
3. Свойство нуля.
Сумма нуля и любого числа равна этому числу: 0 + a = a.
4. Свойство противоположных чисел.
Сумма противоположных чисел равна нулю: a + (-a) = 0.
Выполняем вычисления.
65 + 9 + 5 = (65 + 5) + 9 = 70 + 9 = 79
76 + 8 + 4 = (76 + 4) + 8 = 80 + 8 = 88
36 + 8 + 12 = (8 + 12) + 36 = 20 + 36 = 56
47 + 6 + 24 = (6 + 24) + 47 = 30 + 47 = 77
20 + 27 + 3 + 30 = (27 + 3) + (20 + 30) = 30 + 50 = 80
50 + 19 + 1 + 20 = (19 + 1) + (50 + 20) = 20 + 70 = 90
Оформляем задание в тетрадь.
65 + 9 + 5 = (65 + 5) + 9 = 79
76 + 8 + 4 = (76 + 4) + 8 = 88
36 + 8 + 12 = (8 + 12) + 36 = 20 + 36 = 56
47 + 6 + 24 = (6 + 24) + 47 = 30 + 47 = 77
20 + 27 + 3 + 30 = (27 + 3) + (20 + 30) = 30 + 50 = 80
50 + 19 + 1 + 20 = (19 + 1) + (50 + 20) = 20 + 70 = 90
Номер 2.
Реши с устным объяснением.
Ответ:
Повторим письменные приемы сложения и вычитания в столбик.
Выполняем вычисления с устным объяснением.
43 + 12
Пишем десятки под десятками, а единицы под единицами.
Складываем единицы: 3 + 2 = 5.
Пишем 5 под единицами.
Складываем десятки: 4 + 1 = 5.
Пишем 5 под десятками.
Читаем ответ: сумма равна 55.
57 + 23
Пишем десятки под десятками, а единицы под единицами.
Складываем единицы: 7 + 3 = 10.
Пишем 0 под единицами, а 1 десяток запоминаем (пишем сверху над десятками).
Складываем десятки: 5 + 2 = 7 и ещё 1 десяток, который запоминали, получается 8.
Пишем 8 под десятками.
Читаем ответ: сумма равна 80.
24 + 67
Пишем десятки под десятками, а единицы под единицами.
Складываем единицы: 4 + 7 + 11.
Пишем 1 под единицами, а 1 десяток запоминаем (пишем сверху над десятками).
Складываем десятки: 2 + 6 = 8 и ещё 1 десяток, который запоминали, получается 9.
Пишем 9 под десятками.
Читаем ответ: сумма равна 91.
35 − 21
Пишем десятки под десятками, а единицы под единицами.
Вычитаем единицы: 5 − 1 = 4.
Пишем 4 под единицами.
Вычитаем десятки: 3 − 2 = 1.
Пишем 1 под десятками.
Читаем ответ: разность равна 14.
95 − 65
Пишем десятки под десятками, а единицы под единицами.
Вычитаем единицы: 5 – 5 = 0.
Пишем 0 под единицами.
Вычитаем десятки: 9 − 6 = 3.
Пишем 3 под десятками.
Читаем ответ: разность равна 30.
83 − 26
Пишу десятки под десятками, а единицы под единицами.
Вычитаем единицы: из 3 не можем вычесть 6, поэтому занимаем 1 десяток (над десятками ставим точку, чтобы не забыть о том, что десятков стало на один меньше).
13 − 6 = 7
Пишем 7 под единицами.
Вычитаем десятки: из 8 вычитаем 1, который занимали, получилось 7, тогда 7 − 2 = 5.
Пишем 5 под десятками.
Читаем ответ: разность равна 57.
Оформляем задание в тетрадь.
.jpg)
Номер 3.
Из чисел 8, 5, 6, 2 составь и запиши две суммы так, чтобы значение одной суммы было в 2 раза меньше значения другой.
Ответ:( 8 + 6) : ( 5 + 2 ) = 14 : 7 = 2
Повторим случаи табличного деления, а также названия чисел при сложении.
Составим и запишем две суммы по заданному правилу.
8 + 6
5 + 2
Выполним вычисления и сравним суммы.
8 + 6 = 14
5 + 2 = 7
Чтобы узнать, правильно ли мы составили суммы, нужно результат первой суммы разделить на результат второй.
14 : 7 = 2
Суммы составлены правильно.
Оформляем задание в тетрадь.
(8 + 6) : (5 + 2) = 14 : 7 = 2
Номер 4.
Длина дорожки от дома до беседки 18 м, а от беседки до парника в 2 раза короче. Сколько метров от дома до парника?
Ответ:
Длина от дома до беседки – 18 м.
Длина от беседки до парника - ? В 2р. к
Длина от дома до парника - ?
1) 18 : 2 = 9 (м) – длина дорожки от беседки до парника.
2) 18 + 9 = 27 (м) – длина дорожки от дома до парника.
Ответ: 27 м от дома до парника.
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие задачи в виде краткой записи.
Длина от дома до беседки – 18 м.
Длина от беседки до парника – ? в 2 р. короче.
Длина от дома до парника – ?
Рассуждаем.
Чтобы узнать, чему равна длина дорожки от беседки до парника, нужно длину дорожки от дома до беседки разделить на 2, потому что известно, что длина от беседки до парника в два раза короче.
1) 18 : 2 = 9 (м) – длина дорожки от беседки до парника.
Продолжаем рассуждение.
Чтобы узнать, чему равна длина дорожки от дома до парника, нужно сложить длину дорожки от дома до беседки и длину дорожки от беседки до парника.
2) 18 + 9 = 27 (м) – длина дорожки от дома до парника.
Записываем ответ.
Ответ: 27 м от дома до парника.
Номер 5.
На каникулах Ваня был в спортивном лагере 3 недели, а в деревне у бабушки на 1 неделю больше, чем в лагере. Сколько всего недель Ваня был в спортивном лагере и в деревне?
Ответ:

1) 3 + 1 = 4 (н.) – Ваня был в деревне.
2) 3 + 4 = 7 (н.)
Ответ: 7 недель был в лагере и деревне.
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Оформляем условие задачи в виде краткой записи.
.jpg)
Рассуждаем.
Узнаем, сколько недель Ваня был в деревне, для этого к количеству недель, проведенных в спортивном лагере, прибавим 1 неделю.
1) 3 + 1 = 4 (н.) – Ваня был в деревне.
Продолжаем рассуждение.
Узнаем, сколько недель Ваня был в лагере и в деревне вместе.
2) 3 + 4 = 7 (н.)
Записываем ответ.
Ответ: 7 недель был в лагере и деревне.
Номер 6.
Составь верные равенства и неравенства, используя следующие выражения:
Ответ:
Равенство – это когда одно количество равно другому.
Неравенство – это когда одна сторона выражения не равна второй.
Если носик галочки смотрит направо – это знак больше (>).
Если носик галочки смотри налево – это знак меньше (<).
Знак равенства (=) в математике – символ, который пишется между двумя одинаковыми по своему значению выражениями.
Составляем равенства и неравенства и выполняем вычисления.
18 + 2 = 34 − 14
20 = 20
18 + 2 = 70 − 50
20 = 20
34 − 14 = 70 − 50
20 = 20
18 + 2 > 56 − 50
20 > 6
56 − 50 < 34 − 14
6 < 20
70 − 50 > 56 − 50
20 > 6
Оформляем задание в тетрадь.
.jpg)
Номер 7.
Ответ:
1 см 6 мм = 16мм
16 мм = 16 мм
3 дм 8 см < 40 см
38 см < 40 см
8 дм > 79 см
80 см > 79 см
2 м 1 дм > 1 м 2 дм
21 дм > 12 дм
Равенство – это когда одно количество равно другому.
Неравенство – это когда одна сторона выражения не равна второй.
Если носик галочки смотрит направо - это знак больше (>).
Если носик галочки смотри налево – это знак меньше (<).
Знак равенства (=) в математике- символ, который пишется между двумя одинаковыми по своему значению выражениями.
Выполняем вычисления с пояснениями.
1 см 6 мм = 16 мм, потому что 16 мм = 16 мм.
3 дм 8 см < 40 см, потому что 38 см < 40 см.
8 дм > 79 см, потому что 80 см > 79 см.
2 м 1 дм > 1 м 2 дм, потому что 21 дм > 12 дм.
Оформляем задание в тетрадь.
1 см 6 мм = 16 мм
16 мм = 16 мм
3 дм 8 см < 40 см
38 см < 40 см
8 дм > 79 см
80 см > 79 см
2 м 1 дм > 1 м 2 дм
21 дм > 12 дм
Номер 8.
Начерти ломаную из трех звеньев так, чтобы длина каждого звена была равна 6 см. Узнай длину ломаной.
Ответ:
6 + 6 + 6 = 18 (см) – длина ломаной. Ответ: 18 см общая длина ломаной.
Ломаная – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.
Звенья – отрезки, из которых состоит ломаная.
Отрезок – это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
Длина ломаной – это сумма длин всех её звеньев.
Начертим ломаную заданной длины.
.jpg)
Вычислим длину ломаной.
Чтобы узнать, чему равна длина ломаной, сложим длины каждого из звеньев вместе.
6 + 6 + 6 = 18 (см) – длина ломаной.
Запишем ответ.
Ответ: 18 см.
Номер 9.
Какие фигуры изображены на чертеже? На какие две группы их можно разбить? Сколько способов выполнить это задание тебе удалось найти?.

На чертеже изображены такие фигуры, как треугольники и четырёхугольники.
Фигуры можно разбить на следующие группы:
– розовые или синие фигуры (3,5,7,9 и 1,2,4,6,8);
– треугольники и четырехугольники (1,4,5,8 и 2,3,6,7,9);
– фигуры с прямым углом и без прямого угла (2,3,6,8 и 1,4,5,7,9).
Это здание можно выполнить тремя способами.
Повторим материал о многоугольниках.
Рассмотрим чертеж на полях страницы.
.jpg)
Определим, какие фигуры изображены на чертеже.
На чертеже изображены такие фигуры, как треугольники и четырёхугольники.
Разобьем фигуры на группы.
Фигуры можно разбить на следующие группы:
– розовые или синие фигуры (3,5,7,9 и 1,2,4,6,8);
– треугольники и четырехугольники (1,4,5,8 и 2,3,6,7,9);
– фигуры с прямым углом и без прямого угла (2,3,6,8 и 1,4,5,7,9).
Вывод: это здание можно выполнить тремя способами.
Номер 10.
Красная лента короче синей, а синяя лента короче белой. Какая лента самая длинная?
Ответ:1-й способ решения: Самая длинная лента – белая.
2-й способ решения: Красная лента короче синей ленты, и она не может быть самой длинной. Синяя лента короче белой, и она не может быть самой длинной. Значит, самая длинная лента – белая.
Вспомним, что такое длиннее – короче.
Составим схематический чертеж к задаче.
.jpg)
Рассуждаем.
По условию задачи красная лента короче синей, значит:
красная лента < синей ленты.
По условию задачи синяя лента короче белой, то есть:
синяя лента < белой ленты.
Теперь видно, что:
красная лента < синей ленты < белой ленты.
Следовательно, самая длинная лента – это белая лента, а самая короткая – красная лента.
Записываем ответ.
Ответ: самая длинная лента – белая лента.
Задание внизу страницы
Вычисли, записывая решение столбиком.
Ответ:
Повторим письменные приёмы сложения и вычитания в столбик.
Выполняем вычисления с пояснениями.
28 + 16
Пишем десятки под десятками, а единицы под единицами.
Складываем единицы: 8 + 6 = 14.
Пишем 4 под единицами, а 1 десяток запоминаем (пишем сверху над десятками).
Складываем десятки: 2 + 1 = 3 и ещё 1 десяток, который запоминали, получается 4.
Пишем 4 под десятками.
Читаем ответ: сумма равна 44.
42 − 25
Пишем десятки под десятками, а единицы под единицами.
Вычитаем единицы: из 2 не можем вычесть 5, поэтому занимаем 1 десяток (над десятками ставим точку, чтобы не забыть о том, что десятков стало на один меньше).
12 − 5 = 7
Пишем 7 под единицами.
Вычитаем десятки: из 4 вычитаем 1, которую занимали, получилось 3, тогда 3 − 2 = 1.
Пишем 1 под десятками.
Читаем ответ: разность равна 17.
Далее рассуждаем аналогично.
Оформляем задание в тетрадь.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.