Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 105

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 105

Номер 9.

Из двух листов цветной бумаги можно сделать для украшения елки 6 одинаковых фонариков. Сколько таких фонариков можно сделать из восьми таких же листов бумаги?

Ответ:

математика 3 класс Моро, Бантова - 1 часть страница 105, номер 9

1-й способ решения: 1) 6 : 2 = 3 (ф.) – можно сделать из одного листа бумаги. 2) 3 · 8 = 24 (ф.) – можно сделать Ответ: 24 фонарика можно сделать из восьми таких листов.
2-й способ решения: 6 : 2 · 8 = 3 · 8 = 24 (ф.) – из 8 листов Ответ: 24 фонарика.

Подсказка:

Данная задача: вида «расход 1 листа бумаги, количество бумаги, общее количество фонариков» характеризуется зависимостями между компонентами:

Расход 1 листа бумаги · кол-во бумаги = общее кол-во фонариков.
Общее кол-во фонариков : расход 1 листа бумаги = кол-во бумаги.
Общее кол-во фонариков : кол-во бумаги = расход 1 листа бумаги.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Из таблицы видно, что общее количество фонариков складывается из количества фонариков, которые можно сделать из каждого листа бумаги. Значит, чтобы узнать, каков расход 1 листа бумаги, нужно общее количество фонариков разделить на количество листов бумаги.

6 : 2 = 3 (ф.) – можно сделать из одного листа бумаги.

Шаг 3.
Продолжаем рассуждение.

Общее количество фонариков складывается из количества фонариков, которые можно сделать из каждого листа бумаги. Значит, чтобы узнать, сколько фонариков можно сделать, нужно сложить количество фонариков, сделанных из каждого листа.
Но расход 1 листа бумаги, то есть количество фонариков, которые из 1 листа можно сделать, одинаковый, поэтому сложение одинаковых слагаемых можно заменить умножением.

3 ∙ 8 = 24 (ф.) – можно сделать из 8 листов.

Шаг 4.
Записываем ответ.

Ответ: 24 фонарика.

Решение выражением:
6 : 2 · 8 = 24 (ф.), где 6 : 2 – расход 1 листа бумаги.

Номер 10.

1) 24 л фруктового сока разлили в 8 банок поровну. Сколько надо таких банок, чтобы разлить 18 л сока? 21 л сока?
2) Составь задачу по выражению 12 : (15 : 5).

Ответ:

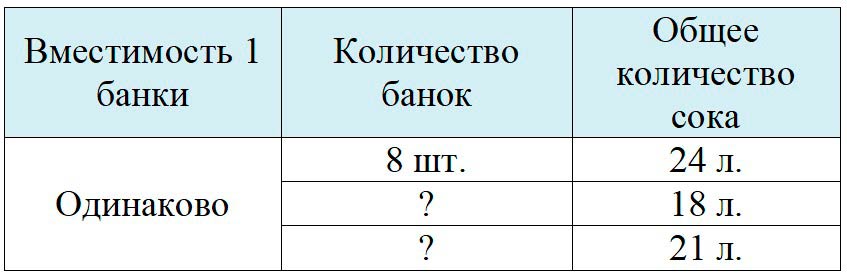
Задача 1: 24 л. – 8 б. 18 л. – ? б. 21 л. – ? б. 1) 24 : 8 = 3 (л) – сока в 1 банке. 2) 18 : 3 = 6 (б.) – для 18 л. сока. 3) 21 : 3 = 7 (б.) – для 21 л. сока. Ответ: 6 банок нужно для 18 литров сока и 7 банок необходимо для 21 литра cока.
Задача 2: 15 кг груш разложили в 5 ящиков. Сколько ящиков нужно, чтобы разложить 12 кг груш? 12 : (15 : 5) = 4 (ящ.) необходимо всего Ответ: нужно 4 ящика для того, чтобы разложить 12 кг груш.

Подсказка:

1) Задача 1. Данная задача: вида «вместимость 1 банки, количество банок, общее количество сока» характеризуется зависимостями между компонентами:

Вместимость банки · количество банок = общее количество сока.
Общее количество сока : вместимость банки = количество банок.
Общее количество сока : количество банок = вместимость банки.

2) Задача 2.
15 кг груш разложили в 5 ящиков. Сколько ящиков нужно, чтобы разложить 12 кг груш?

Задача 1.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Из таблицы видно, что общее количество сока складывается из количества сока в каждой банке. Значит, чтобы узнать, сколько сока вмещается в 1 банку, нужно общее количество сока разделить на количество банок.

24 : 8 = 3 (л) – сока в 1 банке.

Шаг 3.
Продолжаем рассуждение.

Мы узнали, что вместимость 1 банки – 3 литра. Количество сока – 18 литров. Значит, нам известна вместимость 1 банки, общее количество сока, но неизвестно количество банок.
Общее количество сока складывается из количества сока в каждой банке. Значит, чтобы узнать, сколько банок потребовалось для розлива сока, нужно общее количество сока разделить на вместимость 1 банки.

18 : 3 = 6 (б.) – нужно для 18 л. сока.

Шаг 4.
Продолжаем рассуждение.

Мы узнали, что вместимость 1 банки – 3 литра. Количество сока – 21 литр. Значит, нам известна вместимость 1 банки, общее количество сока, но неизвестно количество банок.
Общее количество сока складывается из количества сока в каждой банке. Значит, чтобы узнать, сколько банок потребовалось для розлива сока, нужно общее количество сока разделить на вместимость 1 банки.

21 : 3 = 7 (б.) – нужно для 21 литра.

Шаг 5.
Записываем ответ.

Ответ: 6 банок нужно для 18 л сока и 7 банок – для 21 литра.

Задача 2.

Шаг 1.
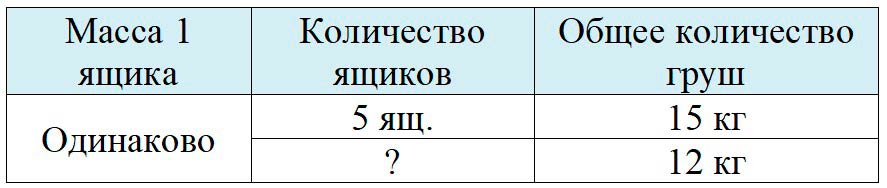
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Общее количество груш складывается из количества груш в каждом ящике. Значит, чтобы узнать, сколько весит один ящик, нужно общее количество груш разделить на количество ящиков.

15 : 5 = 3 (кг) – масса одного ящика.

Шаг 3.
Продолжаем рассуждение.

Мы узнали, что масса одного ящика – 3 кг. Общее количество груш – 12 кг. Значит, нам известна масса одного ящика, общее количество груш, но неизвестно количество ящиков.
Общее количество груш складывается из количества груш в каждом ящике. Значит, чтобы узнать, сколько ящиков потребовалось для всех груш, нужно общее количество груш разделить на массу 1 ящика.

12 : 3 = 4 (ящ.) – нужно для 12 кг груш.

Шаг 4.
Записываем ответ.

Ответ: нужно 4 ящика.

Решение выражением:
12 : (15 : 5) = 4 (ящ.), где 15 : 5 – масса 1 ящика с грушами.

Номер 11.

Ответ:

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.

Шаг 1.
Расставляем порядок действий.

1 2
45 : 5 · 9 = 81
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
56 : 7 · 3 = 24
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
32 : 4 · 8 = 64
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
54 : 9 · 4 = 24
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
8 · 3 : 6 = 4
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
6 · 6 : 9 = 4
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
2 · 9 : 3 = 18
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

1 2
9 · 4 : 6 = 6
В данном уравнении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.

2 1 3
70 − 6 · 7 − 6 = 22
В данном выражении присутствуют действия вычитания и умножение. Вначале выполняем действие умножение, а потом действие вычитание по порядку слева направо.

2 3 1
26 + 8 − 4 · 7 = 6
В данном выражении присутствуют действия сложение, вычитание и умножение. Вначале выполняем действие умножение, потом – сложение, а последним – вычитание.

1 3 2
35 : 5 + 2 · 7 = 21
В данном выражении присутствуют действия сложение, умножение и деление. Вначале выполняем действие деление, потом умножение, а последним – сложение.

1 3 2
8 · 9 − 8 · 5 = 32
В данном выражении присутствуют действия вычитание и умножения. Вначале выполняем действия умножения по порядку слева направо, а последним – вычитание.

1 2
(44 − 8) : 4 = 9
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – деление.

2 1
9 · (10 − 2) = 72
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.

1 2
(8 + 6) : 7 = 2
В данном выражении присутствуют действия сложение и деление, а также скобки. Вначале выполняем действие в скобках – сложение, а потом вне скобок – деление.

2 1
7 · (10 − 9) = 7
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом вне скобок – умножение.

Шаг 2.
Выполняем вычисления по действиям.

1 2
45 : 5 · 9 = 81
1) 45 : 5 = 9,так как 5 · 9 = 45
2) 9 ∙ 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

1 2
56 : 7 · 3 = 24
1) 56 : 7 = 8, так как 7 · 8 = 56
2) 8 ∙ 3 = 24,
где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.

1 2
32 : 4 · 8 = 64
1) 32 : 4 = 8, так как 4 · 8 = 32
2) 8 ∙ 8 = 64,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

1 2
54 : 9 · 4 = 24
1) 54 : 9 = 6, так как 9 · 6 = 54
2) 6 ∙ 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

1 2
8 · 3 : 6 = 4
1) 8 ∙ 3 = 24,
где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
2) 24 : 6 = 4, так как 6 · 4 = 24

1 2
6 · 6 : 9 = 4
1) 6 ∙ 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
2) 36 : 9 = 4, так как 9 · 4 = 36

1 2
2 · 9 : 3 = 18
1) 2 ∙ 9 = 18,
где 2 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
2) 18 : 3 = 6, так как 3 · 6 = 18

1 2
9 · 4 : 6 = 6
1) 9 ∙ 4 = 36,
где 9 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
2) 36 : 6 = 6, так как 6 · 6 = 36

2 1 3
70 − 6 · 7 − 6 = 22
1) 6 ∙ 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

2) 70 - 42 = (70 – 40) – 2 = 30 – 2 = 28

3) 28 - 6 = 20 + (8 – 6) = 20 + 2 = 22

2 3 1
26 + 8 − 4 · 7 = 6
1) 4 ∙ 7 = 28,
где 4 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

2) 26 + 8 = 26 + (4 + 4) = (26 + 4) + 4 = 30 + 4 = 34

3) 34 − 28 = 34 – (24 + 4) = (34 – 24) – 4 = 10 – 4 = 6

1 3 2
35 : 5 + 2 · 7 = 21
1) 35 : 5 = 7, так как 5 · 7 = 35
2) 2 ∙ 7 = 14,
где 2 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
3) 7 + 14 = 21

1 3 2
8 · 9 − 8 · 5 = 32
1) 8 ∙ 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

2) 8 ∙ 5 = 40,
где 8 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

3) 72 − 40 = 32

1 2
(44 − 8) : 4 = 9
1) 44 – 8 = 44 – (4 + 4) = (44 – 4) – 4 = 4 – 4 = 36

2) 36 : 4 = 9, так как 4 · 9 = 36

2 1
9 · (10 − 2) = 72
1) 10 – 2 = 8
2) 9 ∙ 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

1 2
(8 + 6) : 7 = 2
1) 8 + 6 = 14
2) 14 : 7 = 2, так как 7 · 2 = 14

2 1
7 · (10 − 9) = 7
1) 10 – 9 = 1
2) 7 ∙ 1 = 7
При умножении любого числа на 1, получается само число.

Шаг 3.
Оформляем задание в тетрадь.

45 : 5 · 9 = 9 · 9 = 81
56 : 7 · 3 = 8 · 3 = 24
32 : 4 · 8 = 8 · 8 = 64
54 : 9 · 4 = 6 · 4 = 24
8 · 3 : 6 = 24 : 6 = 4
6 · 6 : 9 = 36 : 9 = 4
2 · 9 : 3 = 18 : 3 = 6
9 *·4 : 6 = 36 : 6 = 6

70 – 6 · 7 – 6 = 70 – 6 · 6 = 70 – 36 = 34

26 + 8 – 4 · 7 = 26 + 8 – 28 = 34 – 28 = 6

35 : 5 + 2 · 7 = 7 + 14 = 21
8 · 9 – 8 · 5 = 72 – 40 = 32

(44 – 8) : 4 = 36 : 4 = 9
9 · (10 – 2) = 9 · 8 = 72
(8 + 6) : 7 = 14 : 7 = 2
7 · (10 – 9) = 7 · 1 = 7

Номер 12.

Отличается задание? Переключите год учебника.

2021 2023

1) Запиши все двузначные числа, которые меньше 20. Увеличь каждое из них на 10.
2) Запиши все однозначные числа, которые больше 6. Уменьши каждое из них на 7.

Ответ:

1) 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 10 + 10 = 20 11 + 10 = 21 12 + 10 = 22 13 + 10 = 23 14 + 10 = 24 15 + 10 = 25 16 + 10 = 26 17 + 10 = 27 18 + 10 = 28 19 + 10 = 29
2) 7, 8, 9 7 − 7 = 0 8 − 7 = 1 9 − 7 = 2

Подсказка:

1) Двузначное число – число, запись которого состоит из 2 знаков.

2) Однозначные числа – числа, в записи которого используется 1 знак.

3) Меньше 20, значит, расположенные на луче натуральных чисел левее числа 20.

4) Больше 6, значит расположены на луче натуральных чисел правее 6.

Задание 1.

Шаг 1.
Выпишим числа.

Выпишим все двухзначные числа, которые меньше 20.
Двухзначные числа меньше 20 – это значит, что числа записываются с помощью двух знаков и они расположены на луче натуральных чисел левее числа 20.

Это числа от 10 до 19: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.

Шаг 2.
Увеличить на 10, значит, прибавить 10 единиц.

10 + 10 = 20
11 + 10 = 21
12 + 10 = 22
13 + 10 = 23
14 + 10 = 24
15 + 10 = 25
16 + 10 = 26
17 + 10 = 27
18 + 10 = 28
19 + 10 = 29

Задание 2.

Шаг 1.
Выпишим числа.

Выпишим все однозначные числа, которые больше 6.
Однозначные числа больше 6 – это значит, что числа записываются с помощью одного знака и они расположены на луче натуральных чисел правее числа 6.
Это числа от 7 до 9: 7, 8, 9

Шаг 2.
Уменьшить на 7.

Необходимо вычесть 7 единиц.
7 − 7 = 0
8 − 7 = 1
9 − 7 = 2

1) Запиши все двузначные числа, которые меньше 20. Увеличь каждое из них на 10. 2) Запиши все однозначные числа, которые больше 5. Увеличь каждое из них в 7 раз.

Ответ:

1) 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 10 + 10 = 20 11 + 10 = 21 12 + 10 = 22 13 + 10 = 23 14 + 10 = 24 15 + 10 = 25 16 + 10 = 26 17 + 10 = 27 18 + 10 = 28 19 + 10 = 29
2) 6, 7, 8, 9 6 · 7 = 42 7 · 7 = 49 8 · 7 = 56 9 · 7 = 63

Подсказка:

1) Двузначное число – число, запись которого состоит из 2 знаков.

2) Однозначные числа – числа, в записи которого используется 1 знак.

3) Меньше 20, значит, расположенные на луче натуральных чисел левее числа 20.

4) Больше 5, значит расположены на луче натуральных чисел правее 5.

Задание 1.

Шаг 1.
Выпишем числа.

Шаг 2.
Увеличим на 10.

Значит, прибавим 10 единиц к каждому из заданных чисел.

10 + 10 = 20
11 + 10 = 21
12 + 10 = 22
13 + 10 = 23
14 + 10 = 24
15 + 10 = 25
16 + 10 = 26
17 + 10 = 27
18 + 10 = 28
19 + 10 = 29

Задание 2.

Шаг 1.
Выпишем числа.

Выпишим все однозначные числа, которые больше 5.
Однозначные числа больше 5 – это значит, что числа записываются с помощью одного знака и они расположены на луче натуральных чисел правее числа 5.

Это числа от 6 до 9: 6, 7, 8, 9

Шаг 2.
Увеличим в 7 раз.

Необходимо каждое из данных чисел умножить на 7.

6 · 7 = 42
7 · 7 = 49
8 · 7 = 56
9 · 7 = 63

Номер 13.

Используя каждую пару выражений, составь и запиши верное равенство или неравенство.

Ответ:

70 − (13 + 22) < 70 − 13 + 22 7 + 7 + 7 = 3 ∙ 7
48 + 7 = 63 − 8 12 ∙ 7 = 7 ∙ 12

Подсказка:

1) Равенство – выражение, состоящее из чисел, знаков арифметических действий, скобок и знака равно
2) Неравенство – выражение, состоящее из чисел, знаков арифметических действий, скобок и знаков больше или меньше

Шаг 1.
Рассуждаем.

Сравним 48 + 7 и 63 – 8

Вычислим:
48 + 7 = 48 + (2 + 5) = (48 + 2) + 5 = 50 + 5 = 55

63 – 8 = 63 – (3 + 5) = (63 – 3) – 5 = 60 – 5 = 55

55 = 55, значит, ставим знак равно.
48 + 7 = 63 – 8

Сравним 70 – (13 + 22) и 70 – 13 + 22

Вычислим:
70 – (13 + 22) = 70 – 35 = 70 – (30 + 5) = (70 – 30) – 5 = 40 – 5 = 35

70 – 13 + 22 = 57 + 22 = (50 + 20) + (7 + 2) = 70 + 9 = 79

35 < 79, значит, ставим знак меньше.
70 – (13 + 22) < 70 – 13 + 22

Сравним 3 · 7 и 7 + 7 + 7

3 · 7 = 21, где 3 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

7 + 7 + 7 = 7 · 3 = 21, сумму одинаковых слагаемых можно заменить умножением. 21 = 21, значит ставим знак равно.
3 · 7 = 7 + 7 + 7

Сравним 12 · 7 и 7 · 12
12 · 7 = 7 · 12
Применяем переместительное свойство умножения, значит, ставим знак равно. 12 · 7 = 7 · 12

Шаг 2.
Оформляем задание в тетрадь.

48 + 7 = 63 – 8, так как 55 = 55

70 − (13 + 22) < 70 − 13 + 22, так как 35 < 79

3 ∙ 7 = 7 + 7 + 7, так как сложение одинаковых слагаемых можно заменить умножением и 21 = 21

12 ∙ 7 = 7 ∙ 12
Применяем переместительное свойство умножения.

Номер 14.

Отличается задание? Переключите год учебника.

2021 2023

1) Увеличь на 8 числа: 9; 12; 18; 34; 50; 75; 83; 62.
2) Увеличь в 8 раз числа: 9; 5; 8; 4; 7; 6; 10; 1.

Ответ:

1) 9 + 8 = 17 50 + 8 = 58 12 + 8 = 20 75 + 8 = 83 18 + 8 = 26 83 + 8 = 91 34 + 8 = 42 62 + 8 = 70
2) 9 ∙ 8 = 72 7 ∙ 8 = 56 5 ∙ 8 = 40 6 ∙ 8 = 48 8 ∙ 8 = 64 10 ∙ 8 = 80 4 ∙ 8 = 32 1 ∙ 8 = 8

Подсказка:

1) Увеличь на 8, значит, прибавить 8 единиц.
2) Увеличь в 8 раз, значит, умножь на 8.

Шаг 1.
Увеличим числа на 8.

9 + 8 = 9 + (1 + 7) = (9 + 1) + 7 = 10 + 7 = 17

12 + 8 = (10 + 2) + 8 = 10 + (2 + 8) = 10 + 10 = 20

18 + 8 = 18 + (2 + 6) = (18 + 2) + 6 = 20 + 6 = 26

34 + 8 = 34 + (6 + 2) = (34 + 6) + 2 = 40 + 2 = 42

50 + 8 = 58

75 + 8 = 75 + (5 + 3) = (75 + 5) + 3 = 80 = 3 = 83

62 + 8 = (60 + 2) + 8 = 60 + (2 + 8) = 60 + 10 = 70

Шаг 2.
Увеличим числа в 8 раз.

9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

5 · 8 = 40,
где 5 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

4 · 8 = 32,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

10 · 8 = 80,
где 10 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

1 · 8 = 8,
так как если единицу умножить на любое число, то получится это же число.

1) Уменьши на 8 числа: 9; 12; 18; 34; 50; 75; 83; 62. 2) Уменьши в 8 раз числа: 8; 24; 16; 56; 72; 32.

Ответ:

1) 9 - 8 = 1 12 - 8 = 4 18 - 8 = 10 34 - 8 = 26 50 - 8 = 42 75 - 8 = 67 83 - 8 = 75 62 - 8 = 54
2) 8 : 8 = 1 24 : 8 = 3 16 : 8 = 2 56 : 8 = 7 72 : 8 = 9 32 : 8 = 4

Подсказка:

Повторим таблицу деления.

Шаг 1.
Рассуждаем.

1) Уменьшить на 8, значит, вычесть 8 единиц.
2) Уменьшить в 8 раз, значит, разделить на 8.

Шаг 2.
Выполняем вычисления и оформляем задание в тетрадь.

1)
9 − 8 = 1
12 − 8 = 4
18 − 8 = 10
34 − 8 = 26
50 − 8 = 42
75 − 8 = 67
83 − 8 = 75
62 − 8 = 54

2)
8 : 8 = 1
24 : 8 = 3
16 : 8 = 2
56 : 8 = 7
72 : 8 = 9
32 : 8 = 4

Номер 15.

1) Найди длину стороны квадрата ABCD, периметр которого 8 см. Начерти его и вычисли площадь.
2) Начерти прямоугольник, площадь которого равна площади квадрата ABCD, а длина одной из сторон прямоугольника 1 см.

Ответ:

1) Р = 8 см а = ? см Р = а ∙ 4 а = Р : 4 а = 8 : 4 а = 2 см

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 105, номер 15

S = а ∙ а S = 2 ∙ 2 S = 4 см² Ответ: сторона квадрата 2 см, площадь квадрата 4 см².
2) S = 4 см² а = 1 см b = ? см S = а ∙ b b = S : a b = 4 : 1 b = 4 см

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 105, номер 15-1

Ответ: вторая сторона прямоугольника равна 4 см.

Подсказка:

1) Площадь фигуры измеряется в квадратных единицах измерения.

2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Задание 1.

Шаг 1.
Рассуждаем.

Периметр квадрата равен сумме длин всех сторон. Значит, чтобы вычислить периметр квадрата нужно сложить длины всех сторон квадрата.
Но длина стороны квадрата одинаковы, поэтому, сложение одинаковых слагаемых нужно заменить умножением. Тогда, длину стороны умножаю на количество сторон.
И раз периметр квадрата равен 8 см, то длина стороны вычисляется так: нужно периметр квадрата разделить на количество сторон.

8 : 4 = 2 (см) – длина одной стороны.

Шаг 2.
Начертим.

Начертим квадрат, у которого сторона равна 2 см.

Шаг 3.
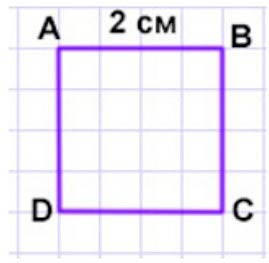
Продолжаем рассуждение.

Чтобы вычислить площадь квадрата, нужно длину стороны умножить на сторону.
2 ∙ 2 = 4 (см²) – площадь квадрата.

Задание 2.

Шаг 1.
Рассуждаем.

Площадь прямоугольника равна площади квадрата ABCD. Значит, площадь квадрата, который мы должны начертить – 4 см².
При это площадь квадрата равна произведению двух сторон. Одна из сторон прямоугольника – 1 см. Соответственно, чтобы узнать длину второй стороны, нужно площадь прямоугольника разделить на длину известной стороны.

4 : 1 см = 4 см – длина второй стороны прямоугольника.

Шаг 2.
Начертим.

Начертим прямоугольник со сторонами 4 см и 1 см.

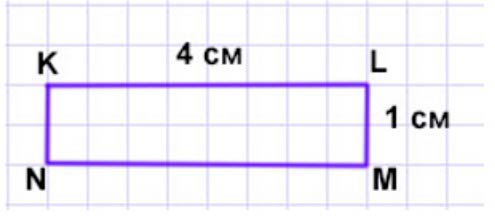
Номер 16.

Ответ:

72 ∙ 0 < 72 ∙ 1 18 : 18 < 18 : 1 64 : 1 > 63 ∙ 1 0 ∙ 32 = 32 ∙ 0

Подсказка:

1) Помни о том, что при умножении любого числа на 1, получается число, которое умножали.

2) Существует еще и другие: умножение числа на 0, и 0 на любое число.

3) Прежде, чем сравнивать значения выражений, вычисли значения выражений в левой и правой части.

Шаг 1.
Рассмотрим выражения.

Сравним 72 · 0 и 72 · 1
72 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
72 · 1 = 71,
так как если любое число умножить на единицу, то получится это же число.
0 < 1, значит, ставим знак меньше.
72 · 0 < 72 · 1

Сравним 64 : 1 и 63 · 1
64 : 1 = 64,
так как если любое число разделить на 1, то получится это же число.
63 · 1 = 63,
так как если любое число умножить на единицу, то получится это же число.
64 > 63, значит, ставим знак больше.
64 : 1 > 63 · 1

Сравним 18 : 18 и 18 : 1
18 : 18 = 1,
так как если любое число разделить на само себя, то получится единица.
18 : 1 = 18,
так как если любое число разделить на единицу, то получится это же число.
1 < 18, значит, ставим знак меньше.
18 : 18 < 18 : 1

Сравним 0 · 32 и 32 · 0
0 · 32 = 0,
так как если 0 умножить на любое число, то получится 0.
32 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
0 = 0, значит, ставим знак равно.
0 · 32 = 32 · 0

Шаг 2.
Оформляем задание в тетрадь.

72 ∙ 0 < 72 ∙ 1
64 : 1 > 63 ∙ 1
18 : 18 < 18 : 1
0 ∙ 32 = 32 ∙ 0

Задания на полях страницы

Начерти:

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 105, задание на полях страницы

Цепочка:

Ответ:

72 : 8 = 9 9 ∙ 4 = 36 36 + 64 = 100 100 − 45 = 55

Подсказка:

1) Выполни действия по порядку.
2) Первая оранжевая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.

Шаг 1.
Выполним устные рассуждения.

72 : 8 = 9, так как 8 · 9 = 72, где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

9 · 4 = 36,
где 9 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

36 + 64 = 100

Складываем единицы. 6 + 4 = 10 – получилось 1 дес. и 0 ед.
Записываем в разряде единиц число 0, а 1 дес. запоминаем.
Складываем десятки. 3 + 6 = 9 и ещё 1 дес., который запомнили 9 + 1 = 10 – получилось десяток. 10 дес. = 1 сот.
Записываем в разряде десятков число 0.
В разряде сотен записываем 1.
Читаем ответ: 100.

100 – 45 = 55

Вычитаем единицы. От числа 0 мы не можем отнять 1.
Занимаем 1 дес. = 10 ед., 10 – 5 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Вычитаем десятки. 1 сот. = 10 ед. Было 10 дес., мы занимали 1 дес, осталось 10 – 1 = 9 дес., 9 – 4 = 5 – получилось десятков.
Записываем в разряде десятков число 5.
Читаем ответ: 55.

Конец страницы