Математика 2 класс учебник Петерсон 2 часть ответы – страница 24

Учебник по математике 2 класс – Перерсон 2 часть.

Тип: ГДЗ, Решебник.
Авторы: Петерсон Л. Г.
Часть: 2.
Год: 2021-2022.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличается задание? Переключите год учебника.

2021 2022

математика 2 класс учебник Петерсон 2 часть страница 24

Номер 9.

Игра «Преобразование слов»
Когда-то в давние времена люди одного царства умели писать только кружки и треугольники. С помощью длинных слов из кружков и треугольников они общались между собой. Разгневался их царь и издал приказ — сократить слова по правилам:

Примени столько раз, сколько возможно, и перейди к 2. Примени столько раз, сколько возможно, и перейди к 3. Примени столько, сколько возможно.
При этом первое правило должно применяться подряд столько раз, сколько возможно, а затем таким же образом должны применяться второе и третье правила.
Рассмотри, правильно ли преобразованы слова:

Пользуясь данным алгоритмом, преобразуй слова:
Придумай свои слова из треугольников и кружков и преобразуй их

Ответ:

Здесь моделируется в игровом варианте так называемый «алгоритм Маркова». Словесное описание алгоритма, заданного картинками, можно дать так:
I. Если в данном слове треугольник находится левее кружка, поменять их местами; применить это правило столько раз, сколько возможно; затем перейти ко второму правилу.
II. Если в полученном слове два кружка стоят рядом, убрать их; применить это правило столько раз, сколько возможно; затем перейти к третьему правилу.
III. Если в полученном слове два треугольника стоят рядом, убрать их; применить это правило столько раз, сколько возможно.
Преобразование данного слова окончено. Полученное слово является результатом преобразования данного слова.

В первом примере в ответе получилось слово, состоящее из одного треугольника, в третьем примере — слово, состоящее из одного кружка, а во втором примере — «пустое слово», не содержащее ни одного кружка и ни одного треугольника. Возможен также вариант, когда в ответе остаются кружок и треугольник.
Подобные преобразования можно выполнять над любой последовательностью треугольников и кружков

математика 2 класс учебник Петерсон 2 часть страница 24, 2022 год

Номер 3.

Выполни вычисления по программам. Чем они похожи и чем различаются?

Составь для каждой схемы выражение. Что ты замечаешь?

Ответ:

а) (564 + 389) + 11 = 953 + 11 = 964

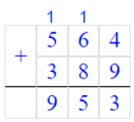
б) 564 + (389 + 11) = 564 + 400 = 964
Выражения состоят из одних и тех же чисел, но отличаются порядком выполнения действий.
Второе выражение вычислить легче.

Номер 4.

Вычисли удобным способом. Обоснуй свой ответ.

(14 + 67) + 3 1 + (99 + 452) (53 + 96) + 4 (25 + 136) + 75 592 + (85 + 108) (37 + 207) + 463 12 + 14 + 16 + 18 (290 + 53) + (47 + 10) 75 + (137 + 25 + 63)

Ответ:

(14 + 67) + 3 = 14 + (67 + 3) = 14 + 70 = 84 1 + (99 + 452) = (1 + 99) + 452 = 100 + 452 = 552 (53 + 96) + 4 = 53 + (96 + 4) = 53 + 100 = 153 (25 + 136) + 75 = (25 + 75) + 136 = 100 + 136 = 236 592 + (85 + 108) = (592 + 108) + 85 = 700 + 85 = 785 (37 + 207) + 463 = (37 + 463) + 207 = 500 + 207 = 707 12 + 14 + 16 + 18 = (12 + 18) + (14 + 16) = 30 + 30 = 60 (290 + 53) + (47 + 10) = (290 + 10) + (53 + 47) = 300 + 100 = 400 75 + (137 + 25 + 63) = (75 + 25) + (137 + 63) = 100 + 200 = 300
Применяем сочетательное свойство сложения.

Номер 5.

а) Покажи прямые углы в классе. Докажи с помощью угольника. б) Найди на рисунке пары перпендикулярных прямых. Сколько прямых углов образуется при их пересечении?

Ответ:

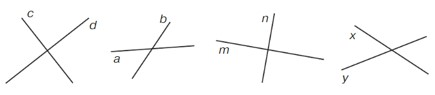
а) Прямые углы в классе есть у парты, стены, у доски и др. Проверь с помощью угольника.
б) Прямые c и d – перпендикулярны, они образуют 4 прямых угла. Прямые m и n – перпендикулярны, они образуют 4 прямых угла.

Номер 6.

У Пети было a книг. Он отдал b книг в школьную библиотеку. Сколько книг у него осталось? Составь выражение и найди его значение, если a = 56, b = 11.

Ответ:

a – b = 56 – 11 = 45 (книг) – осталось у Пети. Ответ: 45 книг.

Номер 7.

У Лены a книг, у Насти b книг, а у Саши c книг. Что означают выражения:

a + b b + c a + c a + b + c a – b b – c

Найди значения этих выражений, если a = 126, b = 82, c = 78.

Ответ:

a + b = 126 + 82 = 208 (книг) – у Лены и Насти вместе; b + c = 82 + 78 = 160 (книг) – у Насти и Саши вместе; a + c = 126 + 78 = 204 (книги) – у Лены и Саши вместе; a + b + c = 126 + 82 + 78 = 126 + 160 = 286 (книг) – всего; a – b = 126 – 82 = 44 (книги) – на сколько больше у Лены, чем у Насти; b – c = 82 – 78 = 82 – 72 – 6 = 10 – 6 = 4 (книги) – на сколько больше у Насти, чем у Саши.

Номер 8.

У Алеши 118 руб., что на 6 руб. меньше, чем у Миши. Хватит ли у них денег, чтобы купить машинку за 240 руб.?

Ответ:

1) 118 + 6 = 118 + 2 + 4 = 120 + 4 = 124 (рубля) – у Миши; 2) 118 + 124 = 242 (рубля) – у мальчиков вместе; 3) 242 > 240 – мальчикам хватит денег, чтобы купить машинку. Ответ: да, хватит.

Номер 9.

Составь слова. Какое из этих слов может быть «лишним»?

УАКЩ СЬЕДЛЬ РЕОХ УЛААК

Ответ:

УАКЩ → ЩУКА СЬЕДЛЬ → СЕЛЬДЬ РЕОХ → ОРЕХ УЛААК → АКУЛА
Лишнее слово ОРЕХ, так как это не рыба.

Конец страницы