Математика 2 класс учебник Моро, Волкова 2 часть ответы – страница 47

- Тип: ГДЗ, Решебник.
- Авторы: Моро М. И., Волкова С. И., Степанова С. В.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Числа от 1 до 100
Умножение и деление
Номер 1.
К каждому примеру на умножение составь два примера на деление.
4 ∙ 3 = 12 6 ∙ 5 = 30 10 ∙ 2 = 20
12 : 4 = ☐ 30 : 6 = ☐ 20 : 10 = ☐
12 : 3 = ☐ 30 : 5 = ☐ 20 : 2 = ☐
4 ∙ 3 = 12 6 ∙ 5 = 30 10 ∙ 2 = 20
12 : 4 = 3 30 : 6 = 5 20 : 10 = 2
12 : 3 = 4 30 : 5 = 6 20 : 2 = 10
Если произведение двух множителей разделить на один из них, то получится другой множитель.
Выполняем вычисления
4 ∙ 3 = 12
12 : 4 = 3
12 : 3 = 4
6 ∙ 5 = 30
30 : 6 = 5
30 : 5 = 6
10 ∙ 2 = 20
20 : 10 = 2
20 : 2 = 10
Оформляем задание в тетрадь
4 ∙ 3 = 12 6 ∙ 5 = 30 10 ∙ 2 = 20
12 : 4 = 3 30 : 6 = 5 20 : 10 = 2
12 : 3 = 4 30 : 5 = 6 20 : 2 = 10
Номер 2.
4 ∙ 7 〇 4 ∙ 9;
0 ∙ 5 〇 1 ∙ 4;
2 ∙ 7 〇 2 ∙ 6;
20 ∙ 3 〇 3 ∙ 20;
6 ∙ 2 〇 6 + 6;
12 + 0 〇 12 − 0.
4 ∙ 7 < 4 ∙ 9, потому что 28 < 36;
0 ∙ 5 < 1 ∙ 4, потому что 0 < 4;
2 ∙ 7 > 2 ∙ 6, потому что 14 > 12;
20 ∙ 3 = 3 ∙ 20, потому что 60 = 60;
6 ∙ 2 = 6 + 6, потому что 12 = 12;
12 + 0 = 12 − 0, потому что 12 = 12.
От перестановки множителей результат умножения не изменяется.
Если 1 умножить на число, получится то же самое число.
Если 0 умножить на число, получится 0.
Выполняем вычисления
4 ∙ 7 < 4 ∙ 9, потому что 28 < 36
0 ∙ 5 < 1 ∙ 4, потому что 0 < 4
2 ∙ 7 > 2 ∙ 6, потому что 14 > 12
20 ∙ 3 = 3 ∙ 20, потому что 60 = 60
6 ∙ 2 = 6 + 6, потому что 12 = 12
12 + 0 = 12 − 0, потому что 12 = 12
Оформляем задание в тетрадь
4 * 7 < 4 * 9
0 * 5 < 1 * 4
2 * 7 > 2 * 6
20 * 3 = 3 * 20
6 * 2 = 6 + 6
12 + 0 = 12 - 0
Номер 3.
1) Цена тетради 3 р. Сколько стоят 5 таких тетрадей?
Сделай схематический чертёж и реши задачу.
2) Составь и реши задачи, обратные данной.

3 ∙ 5 = 15 (р.) - стоят 5 тетрадей.
Ответ: общая стоимость 5 тетрадей составляет 15 рублей.
Обратная задача 1:
На 15 р. купили несколько тетрадей по 3 р. за тетрадь. Сколько тетрадей купили?
1) 15 : 3 = 5 (т.) - купили.
Ответ: 5 тетрадей.
Обратная задача 2:
За 5 тетрадей заплатили 15 рублей. Сколько стоит одна тетрадь?
1) 15 : 5 = 3 (р.) - стоит одна тетрадь.
Ответ: стоимость одной тетради составляет 3 рубля.
Сумму одинаковых слагаемых можно заменить умножением.
Оформляем условие в виде схематического чертежа
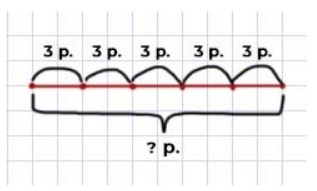
Рассуждаем
Чтобы узнать, сколько стоят 5 тетрадей, нужно стоимость одной тетради умножить на количество тетрадей.
3 * 5 = 15 (р.)
Записываем ответ
Ответ: 15 рублей стоят тетради.
Составляем условие первой задачи обратной данной
За 5 тетрадей заплатили 15 р. Сколько стоит одна такая тетрадь?
Оформляем условие в виде краткой записи
Всего тетрадей – 5 штук
Стоимость – 15 рублей
1 тетрадь - ?
Рассуждаем
Чтобы узнать, сколько стоит одна тетрадь, нужно стоимость всех тетрадей разделить на их количество.
15 : 5 = 3 (р.)
Записываем ответ
Ответ: тетрадь стоит 3 рубля.
Составляем условие второй задачи обратной данной
На 15 р. купили несколько тетрадей. Сколько тетрадей купили, если одна тетрадь стоит 3 рубля?
Оформляем условие в виде краткой записи
Всего тетрадей – ? штук
Стоимость – 15 рублей
1 тетрадь – 3 рубля
Рассуждаем
Чтобы узнать, сколько тетрадей купили, нужно стоимость всех тетрадей разделить на стоимость одной.
15 : 3 = 5 (т.)
Записываем ответ
Ответ: купили 5 тетрадей.
Номер 4.
В киоске за день продали 50 тетрадей, а осталось на 27 тетрадей меньше, чем продали. Сколько всего тетрадей было в киоске до продажи?
Ответ:
1) 50 − 27 = 23 (т.) – осталось.
2) 50 + 23 = 73 (т.) – было.
Ответ: 73 тетради всего было в киоске до продажи.
Повторим действия с двузначными числами.
Вспомним, как составить краткую запись задачи.
Оформляем условие в виде краткой записи

Рассуждаем
Узнаем, сколько тетрадей осталось в киоске после того как продали 50 тетрадей.
1) 50 - 27 = 23 (т.) - осталось в киоске.
Продолжаем рассуждение
Чтобы узнать, сколько всего тетрадей было в киоске до продажи, нужно сложить количество проданных и оставшихся тетрадей вместе.
2) 50 + 23 = 73 (т.)
Записываем ответ
Ответ: было 73 тетради.
Номер 5.
83 – 67;
36 + 29;
52 – 44;
72 + 28.

Повторим действия с двузначными числами.
Выполняем вычисления

Оформляем задание в тетрадь

Номер 6.
90 − (48 − 6);
60 − (52 − 2);
64 + (18 + 2);
70 − (9 + 9);
8 + 9 − 7;
6 + 7 − 8.
90 − (48 − 6) = 90 − 42 = 48;
60 − (52 − 2) = 60 − 50 = 10;
64 + (18 + 2) = 64 + 20 = 84;
70 − (9 + 9) = 70 − 18 = 52;
8 + 9 − 7 = 17 − 7 = 10;
6 + 7 − 8 = 13 − 8 = 5.
Вспомним порядок выполнения действий при нахождении значения числовых выражений со скобками и без них.
Выполняем вычисления
90 - (48 - 6) = 90 - 42 = 90 - 40 - 2 = 50 - 2 = 48
60 - (52 - 2) = 60 - 50 = 10
64 + (18 + 2) = 64 + 20 = 84
70 - (9 + 9) = 70 - 18 = 70 - 10 - 8 = 60 - 8 = 52
8 + 9 - 7 = 17 - 7 = 10
6 + 7 - 8 = 13 - 8 = 13 - 3 - 5 = 10 - 5 = 5
Оформляем задание в тетрадь
90 − (48 − 6) = 90 − 42 = 48
60 − (52 − 2) = 60 − 50 = 10
64 + (18 + 2) = 64 + 20 = 84
70 − (9 + 9) = 70 − 18 = 52
8 + 9 − 7 = 17 − 7 = 10
6 + 7 − 8 = 13 − 8 = 5
Номер 7.
1) Начерти в тетради такой квадрат.
2) Расскажи, что ты знаешь о квадрате, его сторонах, его углах, его осях симметрии.
3) Объясни, как по-разному ученики находили периметр этого квадрата.


1)

2) Прямоугольник, у которого все стороны равны и все углы прямые, называется квадратом, имеет 4 оси симметрии.
3) 1. В первом случае для нахождения периметра на прямой отметили 4 отрезка, длины которых равны длине стороне квадрата, а затем измерили длину получившегося отрезка.
2. Во втором случае для нахождения периметра сложили длины всех сторон квадрата.
3 + 3 + 3 + 3 = 12 (см)
Ответ: периметр квадрат равен 12 см.
3. В третьем случае для нахождения периметра умножили длину стороны квадрата на число сторон.
3 ∙ 4 = 12 (см)
Ответ: периметр квадрат равен 12 см.
Вспомним материал о многоугольниках, вспомни, как найти периметр разными способами.
Ось симметрии фигуры - это прямая, которая делит фигуру на две симметричные части (если по этой прямой перегнуть фигуру, то ее части наложатся друг на друга).
Начертим квадрат как на полях страницы
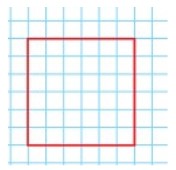
Расскажем, что знаем о квадрате
Прямоугольник, у которого все стороны равны и все углы прямые, называется квадратом. Квадрат имеет 4 оси симметрии.
Оси симметрии квадрата:
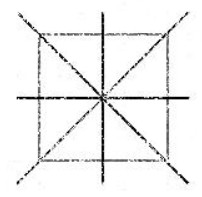
Объясним, как находили периметр данного квадрата первым способом
Нашли сумму всех сторон квадрата. Сложили длины всех сторон.
3 + 3 + 3 + 3 = 12 (см)
Объясним, как находили периметр данного квадрата вторым способом
Длину одной стороны умножили на 4.
По 3 см взяли 4 раза.
3 * 4 = 12 (см)
Оформим задание в тетрадь
1)
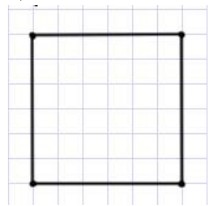
2) Прямоугольник, у которого все стороны равны и все углы прямые, называется квадратом, имеет 4 оси симметрии.
3)
1. В первом случае для нахождения периметра на прямой отметили 4 отрезка, длины которых равны длине стороне квадрата, а затем измерили длину получившегося отрезка.
2. Во втором случае для нахождения периметра сложили длины всех сторон квадрата.
3 + 3 + 3 + 3 = 12 (см)
Ответ: 12 см.
3. В третьем случае для нахождения периметра умножили длину стороны квадрата на число сторон.
3 ∙ 4 = 12 (см)
Ответ: 12 см.
Номер 8.
Вычисли и выполни проверку.
28 + 63;
75 – 49;
67 + 26;
94 – 48.

Повтори действия с двузначными числами.
Выполняем вычисления
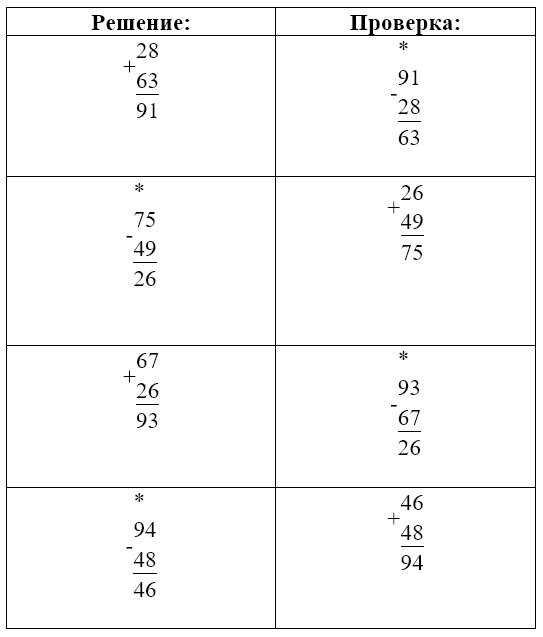
Оформляем задание в тетрадь
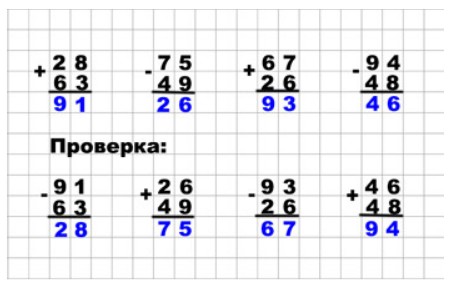
Задание внизу страницы.
5 · 4 = ☐
20 : ☐ = 5
☐ : 4 = 5
4 · 5 = ☐
5 ∙ 4 = 20;
20 : 4 = 5;
20 : 4 = 5;
4 ∙ 5 = 20.
Умножение - это сложение одинаковых слагаемых.
Деление - действие, обратное умножению.
Выполняем вычисления
5 * 4 = 5 + 5 + 5 + 5 = 20
20 : 4 = 5
20 : 4 = 5
4 * 5 = 20
Оформляем задание в тетрадь
5 * 4 = 20
20 : 4 = 5
20 : 4 = 5
4 * 5 = 20
Задание на полях страницы.
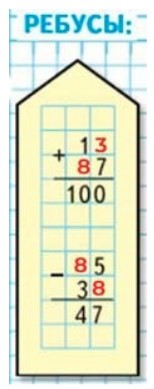
Ребусы:


Вспомни действия с двузначными числами.
Рассмотрим ребус
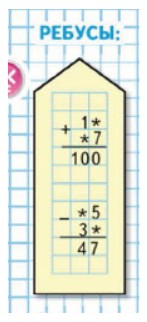
Выполним вычисления и оформим задание в тетрадь
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.