Математика 6 класс учебник Виленкин, Жохов 2 часть ответы – проверочная работа на 137-138 страницах

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 2.
- Год: 2023-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Проверьте себя
Проверочная работа (итоговая) № 1.
Номер 1.
Вычислите:
а) 6,8 + 2,6;
б) 8,4 – 3,7;
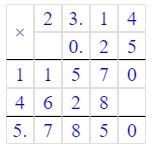
в) 7,7 · 0,53;
г) 67,2 : 0,48;
д) (3,72 + 4,56) + 6,28;
е) 4,33 · 7,92 + 4,33 · 2,18.
а) 6,8 + 2,6 = 9,4
б) 8,4 – 3,7 = 4,7
в) 7,7 · 0,53 = 4,081
г) 67,2 : 0,48 = 6720 : 48 = 140
д) (3,72 + 4,56) + 6,28 = (3,72 + 6,28) + 4,56 = 10 + 4,56 = 14,56
е) 4,33 · 7,92 + 4,33 · 2,18 = 4,33 ∙ (7,92 + 2,18) = 4,33 ∙ 10,1 = 43,733

Номер 2.
Найдите:
а) 10 % от 82,6;
б) 25 % от 23,14.
а) 82,6 ∙ 10% = 82,6 ∙ 0,1 = 8,26 – это 10 % от 82,6;
б) 23,14 ∙ 25% = 23,14 ∙ 0,25 = 5,785 – это 25 % от 23,14.
Номер 3.
Найдите число, если:
а) 40 % числа равно 59,5;
б) 16 % числа равно 47,4.
а) 40 % числа равно 59,5, то число равно:
59,5 : 40% = 59,5 : 0,4 = 595 : 4 = 148,75.
б) 16 % числа равно 47,4, то число равно:
47,4 : 16% = 47,4 : 0,16 = 4740 : 16 = 296,25

Номер 4.
Найдите наибольший общий делитель и наименьшее общее кратное чисел:
а) 16 и 12;
б) 18 и 24.
а) НОД (16; 12) = 2 ∙ 2 = 4; НОК (16; 12) = 16 ∙ 3 = 48.

НОД (18; 24) = 2 ∙ 3 = 6; НОК (18; 24) = 18 ∙ 2 ∙ 2 = 36 ∙ 2 = 72.
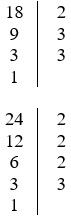
Номер 5.
Найдите значение выражения:
а) 7/15 + 3/10;
б) 7/15 – 3/10;
в) 5/12 ∙ 9/20;
г) 5/12 : 9/20;
д) (5/7 + 314/18) + 2/7;
е) 1619/40 – (13 + 119/40).
а) 7/15 + 3/10 = 14/30 + 9/30 = 23/30
б) 7/15 – 3/10 = 14/30 – 9/30 = 5/30 = 1/6
в) 5/12 ∙ 9/20 = (5 ∙ 3 ∙ 3)/(3 ∙ 4 ∙ 4 ∙ 5) = 3/16
г) 5/12 : 9/20 = 5/12 ∙ 20/9 = (5 ∙ 4 ∙ 5)/(3∙ 4∙ 9) = 25/27
д) (5/7 + 314/18) + 2/7 = (5/7 + 2/7) + 314/18 = 7/7 + 37/9 = 1 + 37/9 = 47/9
е) 1619/40 – (13 + 119/40) = (1619/40 – 119/40) – 13 = 15 – 13 = 2
Номер 6.
Представьте обыкновенные дроби в виде десятичных:
1/8, 1/20, 5/4, 15/30, 85/68, 17/625.
1/8 = 125/1000 = 0,125
1/20 = 5/100 = 0,05
5/4 = 11/4 = 125/100 = 1,25
15/30 = 1/2 = 50/100 = 0,5
85/68 = 117/68 = 11/4 = 125/100 = 1,25
17/625 = 0,0272

Номер 7.
Представьте обыкновенные дроби в виде десятичных:
Во сколько раз 1/4 ч меньше 1/8 сут?
1/8 сут. = 24 : 8 = 3 ч
3 ∶ 1/4 = 3 ∙ 4/1 = 12 (раз) – во сколько раз 1/4 ч меньше 1/8 сут.
Ответ: в 12 раз 1/4 ч меньше 1/8 сут.
Номер 8.
На сколько 1/5 км больше 1/10 м?
Ответ:1/5 км = 1000 : 5 = 200 м
200 – 1/10 = 1999/10 = 199,9 (м) – на сколько 1/5 км больше 1/10 м.
Ответ: на 199,9 м 1/5 км больше 1/10 м.
Номер 9.
Выполните действия:
а) –4 + 1,3;
б) –5,6 – (–8);
в) –63/4 – (–0,75);
г) –0,3 · (–0,3);
д) –5 · 20;
е) 23/4 ∙ (–3,7) ∙ 0;
ж) (–42) : 6;
з) –36 : (–0,6);
и) (–123/11) ∶ (–3).
а) –4 + 1,3 = –(4 – 1,3) = –2,7
б) –5,6 – (–8) = –5,6 + 8 = 8 – 5,6 = 2,4
в) –63/4 – (–0,75) = –6,75 + 0,75 = –6
г) –0,3 · (–0,3) = 0,3 ∙ 0,3 = 0,09
д) –5 · 20 = –100
е) 23/4 ∙ (–3,7) ∙ 0 = 0
ж) (–42) : 6 = –7
з) –36 : (–0,6) = 360 : 6 = 60
и) (–123/11) : (–3) = (12 + 3/11) : 3 = 12 ∶ 3 + 3/11 ∙ 1/3 = 4 + 1/11 = 41/11
Номер 10.
Вычислите.
а) |27,8| – |–27,8|;
б) |7/9|∙ |–21/4|;
в) 0,36 : |–0,18|.
а) |27,8| – |–27,8| = 27,8 – 27,8 = 0
б) |7/9|∙ |–21/4| = 7/9 ∙ 9/4 = 7/4 = 13/4 = 1,75
в) 0,36 : |–0,18| = 0,36 : 0,18 = 36 : 18 = 2
Номер 11.
а) Является ли диагональ квадрата его осью симметрии?
б) Является ли точка пересечения диагоналей квадрата его центром симметрии?
а) Да, диагональ квадрата является его осью симметрии.
б) Да, точка пересечения диагоналей квадрата является его центром симметрии.
Номер 12.
Найдите объём прямоугольного параллелепипеда с измерениями 12 см, 4,5 дм и 0,4 м.
Ответ:а = 12 см,
b = 4,5 дм = 45 cм
с = 0,4 м = 40 см
V – ?
12 ∙ 45 ∙ 40 = (12 ∙ 40) ∙ 45 = 480 ∙ 45 = 21 600 (см3) = 216 (дм3) – объём прямоугольного параллелепипеда.
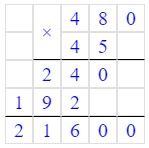
Ответ: объём прямоугольного параллелепипеда равен 216 дм3.
Проверочная работа (итоговая) № 2.
Номер 1.
Упростите выражение:
а) –с + с;
б) –с – с;
в) –с – (–с);
г) 0 – (–с);
д) 0 + (–с);
е) –с · (–1);
ж) –с · 0;
з) –с : (–с), c ≠ 0;
и) с : (–с), c ≠ 0.
а) –с + с = с – с = 0
б) –с – с = –(с + с) = –2с
в) –с – (–с) = –с + с = 0
г) 0 – (–с) = 0 + с = с
д) 0 + (–с) = 0 – с = –с
е) –с · (–1) = с
ж) –с · 0 = 0
з) –с : (–с) = 1, если c ≠ 0;
и) с : (–с) = –1, если c ≠ 0.
Номер 2.
В магазин поступило 600 учебников. В первый день продали 2/5, а на следующий день 3/8 всего количества учебников. Сколько учебников осталось?
Ответ:
Способ решения 1:
1) 2/5 + 3/8 = 16/40 + 15/40 = 31/40 (часть) – учебников продали за два дня;
2) 1 – 31/40 = 40/40 – 31/40 = 9/40 (часть) – учебников осталось;
3) 600 ∙ 9/40 = 15 ∙ 9 = 135 (уч.) – осталось.
Ответ: осталось 135 учебников.
Способ решения 2:
1) 600 ∙ 2/5 = 120 ∙ 2 = 240 (уч.) – продали в первый день;
2) 600 ∙ 3/8 = 75∙3 = 225 (уч.) – продали во второй день;
3) 240 + 225 = 465 (уч.) – продали за два дня;
4) 600 – 465 = 135 (уч.) – осталось.
Ответ: осталось 135 учебников.
Номер 3.
Разность двух чисел составляет 4/5 уменьшаемого. На сколько процентов уменьшаемое больше вычитаемого?
Ответ:
Способ решения 1:
Пусть уменьшаемое равно х, а вычитаемое – у. Тогда разность х и у равна 4/5х.
Составим уравнение:
x – y = 4/5x
x – 4/5x = y
1/5x = y
y = 0,2x
Значит вычитаемое составляет 20% от уменьшаемого.
100% – 20% = 80% – на сколько процентов уменьшаемое больше вычитаемого.
Ответ: на 80% уменьшаемое больше вычитаемого.
Способ решения 2:
По условию задачи знаем, что разность уменьшаемого и вычитаемого равна 4/5 от уменьшаемого или 80% от уменьшаемого, так же уменьшаемое больше вычитаемого на их разность. Следовательно, уменьшаемое больше вычитаемого на 80%.
4/5 ∙ 100% = 400/5% = 80%
Ответ: на 80% уменьшаемое больше вычитаемого.
Номер 4.
Сумма двух чисел равна 9,1 и одно из них составляет 2/5 другого. Найдите эти числа.
Ответ:Пусть первое число равно х, тогда второе – 2/5x. Известно, что их сумма равна 9,1.
Составим уравнение:
x + 2/5x = 9,1
12/5x = 9,1
7/5x = 91/10
x = 91/10 ∶ 7/5
x = 91/10 ∙ 5/7
x = 13/2
x = 61/2 = 6,5
6,5 – это первое число;
9,1 – 6,5 = 2,6 – это второе число.
Ответ: первое число – 6,5 и второе число – 2,6.
Номер 5.
За 6 ч студенты собрали 40 % клубники. За какое время они соберут остальную клубнику, если будут работать с той же производительностью?
Ответ:100% - 40% = 60% - клубники осталось собрать.
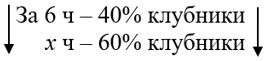
Составим пропорцию:
6/x = 40/60
6/x = 2/3
2x = 6 ∙ 3
2x = 18
x = 18 : 2
x = 9
9 ч – соберут студенты остальную клубнику.
Ответ: за 9 часов студенты соберут остальную клубнику.
Номер 6.
Резервуар водонапорной башни наполняется за 4 ч. На рисунке 3 приведён график наполнения резервуара. Какая часть резервуара наполнилась за первые 3 ч? Выберите ответ.
а) 80 %;
б) 90 %;
в) 87,5 %;
г) другой ответ.
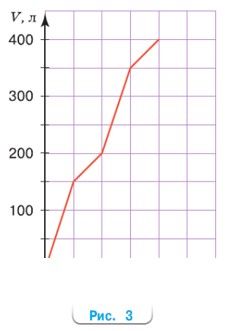
Объём резервуара – 400 л
Наполнилось за 3 ч – 350 л
Какая часть наполнилась за 3 ч – ?
350/400 ∙ 100% = 350/4% = 87,5% – часть резервуара наполнилась за первые 3 ч.
Верный ответ в) 87,5 %.
Ответ: в) 87,5 %.
Номер 7.
На рисунке 4 приведён график движения пешехода в течение трёх часов. Чему равна средняя скорость пешехода с 14.00 до 16.00? Выберите ответ.
а) 3,5 км/ч;
б) 4,5 км/ч;
в) 4 км/ч;
г) другой ответ.
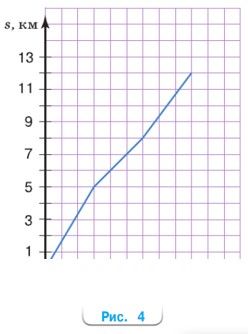
За 3 часа пешеход прошёл 12 км.
12 : 3 = 4 (км/ч) – средняя скорость пешехода за 3 часа.
Верный ответ: в) 4 км/ч.
Ответ: в) 4 км/ч.
Номер 8.
Решите пропорцию:
а) 25 : 75 = x : 27,3;
б) x ∶ 1/4 = 1 ∶ 0,25
а) 25 : 75 = x : 27,3
75х = 25 ∙ 27,3
х = (25 ∙ 27,3)/75
х = (1 ∙ 27,3)/3
х = 9,1
Ответ: х = 9,1.
б) x ∶ 1/4 = 1 ∶ 0,25
0,25x = 1/4 ∙ 1
0,25x = 0,25
x = 0,25 : 0,25
x = 1
Ответ: х = 1.
Номер 9.
Площадь круглого журнального столика равна 188,4 см2. Найдите площадь круглого обеденного стола, радиус которого в 2 раза больше радиуса журнального столика. Принять π равным 3,14.
Ответ:
Пусть радиус журнального столика равна х см, тогда радиус обеденного столика равна 2х см. Площадь журнального столика равна πх2, а площадь обеденного столика равна π ∙ (2x)2 = π ∙ 4 ∙ x2 = 4πx2. Известно, что площадь журнального столика равна 188,4 см2.
В буквенное выражение 4πx2 подставим значение πx2 = 188,4 см2.
4πx2 = 4 ∙ 188,4 = 753,6 (см2)

Значит, площадь обеденного стола равна 753,6 см2.
Ответ: площадь обеденного стола равна 753,6 см2.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.