Математика 6 класс учебник Виленкин, Жохов 2 часть ответы – применяем математику на 97 странице

Пусть собственная скорость теплохода х км/ч, тогда по течению – (х + 3) км/ч, а против течения (х – 3) км/ч. Известно, что за 5 ч ему надо проплыть путь по течению реки, а за 7 ч вернуться обратно.

Составим уравнение:
5(х + 3) = 7(х – 3)
5х + 15 = 7х – 21
7х – 5х = 15 + 21
2х = 36
х = 36 : 2
х = 18
18 км/ч – собственная скорость теплохода.
Ответ: собственная скорость экскурсионного теплохода равна 18 км/ч.

Пусть средняя скорость первого дирижабля равна х км/ч, тогда средняя скорость второго – (х + 20) км/ч. Известно, что расстояние между ними 770 км и должны они доставить груз одновременно через 5 ч на комбинат, выехав навстречу друг другу.
Составим уравнение:
х + х + 20 = 770 : 5
2х = 154 – 20
2х = 134
х = 134 : 2
х = 67
67 км/ч – средняя скорость первого дирижабля;
67 + 20 = 87 (км/ч) – средняя скорость второго дирижабля.
Ответ: средняя скорость первого дирижабля равна 67 км/ч и средняя скорость второго дирижабля равна 87 км/ч.

Пусть работники отработали х дней, тогда неотработанных дней было (30 – х). За все отработанные дни работники получили 48х франков, а за неотработанные вычли 12(30 – х) франков. Известно, что работникам ничего не выплатили.
Составим уравнение:
48х = 12(30 – х)
48х = 360 – 12х
48х + 12х = 360
60х = 360
х = 360 : 60
х = 6
6 дней – рабочие;
30 – 6 = 24 (дня) – нерабочие.
Ответ: 6 дней они отработали.

Пусть всего х кроликов, тогда фазанов – (1000 – х). У одного кролика 4 ноги, значит всего у кроликов 4х ног. У одного фазана 2 ноги, тогда у всех фазанов 2(1000 – х) ног. Известно, что всего 3150 ног.
Составим уравнение:
4х + 2(1000 – х) = 3150
4х + 2000 – 2х = 3150
2х = 3150 – 2000
2х = 1150
х = 1150 : 2
х = 575
575 кроликов;
1000 – 575 = 425 – фазанов.
Ответ: 575 кроликов и 425 фазанов.

М = 4000 р.
N = 25 дн.
S = 7,5% = 0,075
Р – ?
P = 1/300 ∙ 4000 · 25 · 0,075 = 40/3 ∙ 25 ∙ 0,075 = (1000 ∙ 0,075)/3 = 75/3 = 25 (р.)
Ответ: пени за 25 дней просрочки равно 25 рублей.

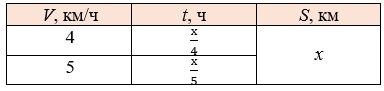
Пусть расстояние до станции х км. Если он будет идти со скоростью 4 км/ч, то затратит времени х/4 ч и опоздает на 30 мин = 1/2 ч, если будет идти со скоростью 5 км/ч то затратит - х/5 и придёт раньше на 6 мин = 1/10 ч.
Составим уравнение:
х/4 – 1/2 = х/5 + 1/10 | ∙ 20
5х – 10 = 4х + 2
5х – 4х = 2 + 10
х = 12
12 км расстояние, которое должен пройти турист.
Ответ: 12 км должен пройти турист.

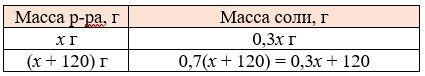
Пусть первоначальная масса раствора х г, тогда масса соли в растворе – 0,3х г. Если добавить 120 г соли, то масса раствора станет (х + 120) г, а соли в растворе станет (0,7(х + 120)) г или (0,3х + 120) г.
Составим уравнение:
0,7(х + 120) = 0,3х + 120
0,7х + 84 = 0,3х + 120
0,7х – 0,3х = 120 – 84
0,4х = 36
х = 36 : 0,4 = 360 : 4
х = 90
90 г – масса раствора;
0,3 ∙ 90 = 27 (г) – масса соли в растворе.
Ответ: 90 г первоначальная масса раствора и 27 г масса соли в растворе.

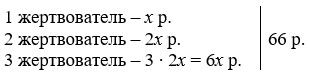
Пусть первый жертвователь дал х рупий, тогда второй – 2х рупий, а третий – 3 ∙ 2х = 6х рупий. Известно, что вместе они дали 66 рупий.
Составим уравнение:
х + 2х + 6х = 66
9х = 66
х = 66 : 9
х = 73/9=71/3
71/3 рупия – дал первый;
71/3 ∙ 2 = 22/3 ∙ 2 = 44/3 = 142/3 (рупий) – дал второй;
44/3 ∙ 3 = 44 (рупия) – дал третий.
Ответ: 71/3 рупий дал первый жертвователь, 142/3 рупий дал второй жертвователь и 44 рупия дал третий жертвователь.

Пусть в первом квартале было получено прибыли х млн. руб, тогда во второй квартал – (х + 0,1х = 1,1х) млн. руб. Известно, что всего за полугодие было получено 126 млн. руб.
Составим уравнение:
х + 1,1х = 126
2,1х = 126
х = 126 : 2,1
х = 1260 : 21
х = 60
60 млн. руб – прибыль в первом квартале;
1,1 ∙ 60 = 66 (руб.) – прибыль во втором квартале.
Ответ: 66 млн. рублей прибыли получила фирма во втором квартале.

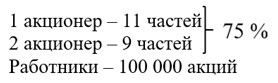
1) 100% – 75% = 25% – принадлежат работникам агрохолдинга или составляет 100 000 акций;
2) 100 000 : 25% = 100 000 : 0,25 = 10 000 000 : 25 = 400 000 (акций) – всего;
3) 400 000 – 100 000 = 300 000 (акций) – у двух акционеров;
4) 11 + 9 = 20 (частей) – составляют 300 000 акций;
5) 300 000 : 20 = 15 000 (акций) – 1 часть;
6) 15 000 ∙ 11 = 165 000 (акций) – у первого акционера;
7) 15 000 ∙ 9 = 135 000 (акций) – у второго акционера.
Ответ: 165 000 акций у первого акционера и 135 000 акций у второго акционера.