Математика 6 класс учебник Виленкин, Жохов 2 часть ответы – применяем математику на 120 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 2.
- Год: 2023-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Применяем математику
Номер 1.
Группа шестиклассников отправились на экскурсию в два заповедника на автобусе.
1) Используя график движения группы (рис. 6.39), определите:
а) время выезда группы на экскурсию;
б) время возвращения домой;
в) продолжительность экскурсии;
г) сколько длился переезд из первого заповедника во второй;
д) сколько часов длилось посещение второго заповедника;
е) сколько времени автобус находился на стоянке.
2) Рассчитайте среднюю скорость движения автобусов на каждом участке маршрута.
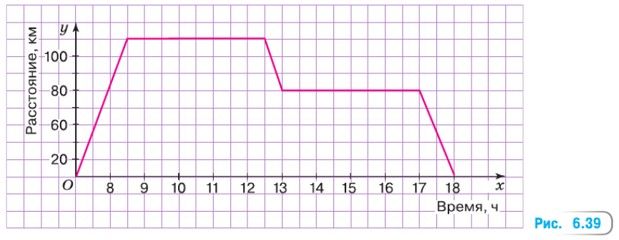
1) а) 7 ч – время выезда группы на экскурсию;
б) 18 ч – время возвращения домой;
в) 18 ч – 7 ч = 11 ч – продолжительность экскурсии;
г) 30 мин – сколько длился переезд из первого заповедника во второй;
д) 4 ч – длилось посещение второго заповедника;
е) 4 ч + 4 ч = 8 ч – автобус находился на стоянке.
2) 1) 120 : 1,5 = 1200 : 15 = 80 (км/ч) – средняя скорость с 7 ч до 8,5 ч;
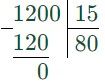
2) 60 : 0,5 = 600 : 5 = 120 (км/ч) – средняя скорость с 12,5 ч до 13 ч;
3) 80 : 1 = 80 (км/ч) – средняя скорость с 17 ч до 18 ч.
Пояснение: в графике ошибка – не верно расставлено расстояние.
Номер 2.
В выходные дни для поездки на водохранилище, которое расположено в 200 км от дома, папа хочет арендовать автомобиль на двое суток. В таблице приведены характеристики трёх автомобилей и стоимость их аренды.
Сколько рублей заплатит папа за аренду и топливо при выборе самого дешёвого варианта, если цена дизельного топлива за литр – 47,3 р., бензина АИ-92 – 42,5 р., бензина АИ-95 – 46,7 р.?
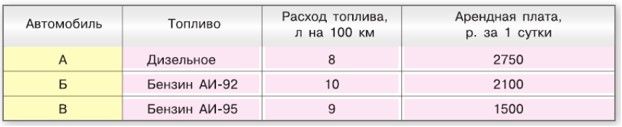
200 км ∙ 2 = 400 км – весь путь туда и обратно.
Автомобиль А:
1) 8 : 100 ∙ 400 = 8 ∙ 4 = 32 (л) – израсходуется бензина за 2 дня;
2) 47,3 ∙ 32 = 1513,6 (р.) – на топливо;
3) 2750 ∙ 2 = 5500 (р.) – аренда за 2 дня;
4) 1513,6 + 5500 = 7013,6 (р.) – общая сумма.
Автомобиль Б:
1) 10 : 100 ∙ 400 = 10 ∙ 4 = 40 (л) – израсходуется бензина за 2 дня;
2) 42,5 ∙ 40 = 1700 (р.) – на топливо;
3) 2100 ∙ 2 = 4200 (р.) – аренда за 2 дня;
4) 1700 + 4200 = 5900 (р.) – общая сумма.
Автомобиль В:
1) 9 : 100 ∙ 400 = 9 ∙ 4 = 36 (л) – израсходуется бензина за 2 дня;
2) 46,7 ∙ 36 = 1681,2 (р.) – на топливо;
3) 1500 ∙ 2 = 3000 (р.) – аренда за 2 дня;
4) 1681,2 + 3000 = 4681,2 (р.) – общая сумма.

Самый дешёвый вариант под В.
Ответ: 4681,2 рублей заплатит папа.
Номер 3.
Родители Миши решили застраховать свою дачу. Они оценили свой дом в 4 млн р. и имущество – в 1 млн р. Одна страховая компания предлагает страхование на год на следующих условиях: дом – 0,2 % стоимости и имущество – 0,7 % стоимости. Другая страховая компания предлагает страховой полис на 3 года за 36 900 р., который включает страхование дома и имущества. В какой компании им выгоднее застраховать дом и имущество на 5 лет?
Ответ:Первая страховая компания:
1) 4 000 000 ∙ 0,002 + 1 000 000 ∙ 0,007 = 8000 + 7000 = 15 000 (руб.) – страхование на год;
2) 15 000 ∙ 5 = 75 000 (р.) – страхование на 5 лет.
Вторая страховая компания:
36 900 ∙ 2 = 73 800 (р.) – страхование на 6 лет.
75 000 р. > 73 800 р. – во второй компании выгоднее застраховать дом и имущество на 6 лет.
Ответ: во второй компании выгоднее застраховать дом и имущество.
Номер 4.
Бабушка попросила Ярослава, Нику и Кирилла прополоть две квадратные клумбы. У первой клумбы сторона 0,9 м, а у другой - 1,8 м. Ярослав рассудил так: первая клумба в 2 раза меньше второй, поэтому я прополю её, а Ника и Кирилл пусть прополют вторую клумбу, и это будет справедливо, так как я старший брат. Прав ли Ярослав?
Ответ:1) 0,92 = 0,81 (м2) – площадь первой клумбы или сколько прополет Ярослав;
2) 1,82 = 3,24 (м2) – площадь второй клумбы;
3) 3,24 : 2 = 1,62 (м2) – прополют Ника и Кирилл по отдельности.
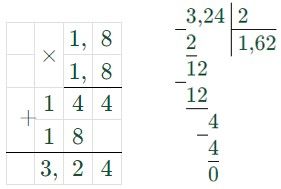
Ярослав не прав, так как он прополет в 2 раза меньше, чем Ника и Кирилл (1,62 : 0,81 = 162 : 81 = 2)
Ответ: Ярослав не прав.
Номер 5.
Спелеологи обследовали пещеру, вход и выход в которую совпадают и находятся на склоне горы на высоте 200 м над уровнем моря. График движения группы показан на рисунке 6.40, где на оси у отмечена высота в метрах над уровнем моря, а на оси x - время в часах. Используя график, ответьте на вопросы.
а) В какое время спелеологи вышли со стоянки? На какой высоте была стоянка спелеологов?
б) Сколько времени спелеологи поднимались ко входу в пещеру?
в) До какой глубины они обследовали пещеру?
г) Как долго осуществлялся спуск в пещере до нулевой высоты?
д) Как долго находились спелеологи на максимальной глубине?
е) В какое время спелеологи начали движение с максимальной глубины?
ж) На каком участке скорость передвижения спелеологов была больше? Сколько времени заняло это передвижение?
з) На какие ещё вопросы можно ответить по этому графику?
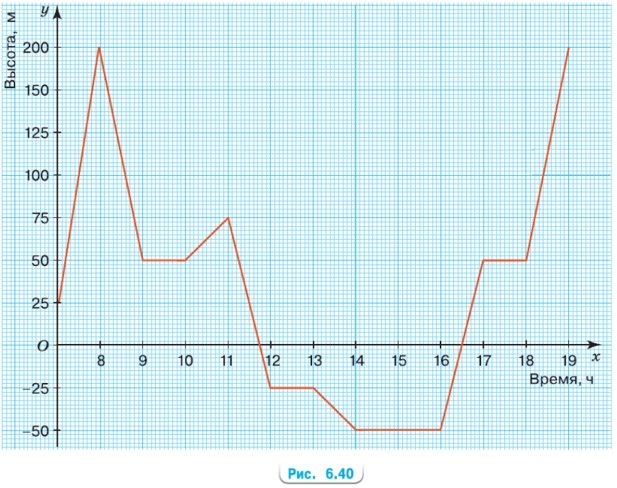
а) В 7 утра - спелеологи вышли со стоянки.
На высоте 25 м была стоянка спелеологов.
б) 1 час спелеологи поднимались ко входу в пещеру.
в) Они обследовали пещеру до глубины 50 м ниже уровня моря.
г) 3,7 часа или 3 часа 42 мин осуществлялся спуск в пещере до нулевой высоты.
д) 2 ч находились спелеологи на максимальной глубине.
е) В 16 ч спелеологи начали движение с максимальной глубины.
ж) При подъёме на входе в пещеру (с 7 – 8 ч) скорость передвижения спелеологов была больше. Оно заняло 1 час.
з) Дополнительные вопросы:
1) Как долго длился подъём к выходу? (3 часа)
2) Сколько по времени заняло всё обследование пещеры? (12 часов)
3) Сколько было остановок? (4 остановки) Общее время остановок? (5 ч)
Номер 6.
Альпинисты планируют подъём в горы на высоту 5860 м. Через каждый километр подъёма термометр показывает примерно на 6 °С меньше. Постройте график изменения температуры воздуха при подъёме на эту высоту, если у подножия горы 14 °С.
Ответ: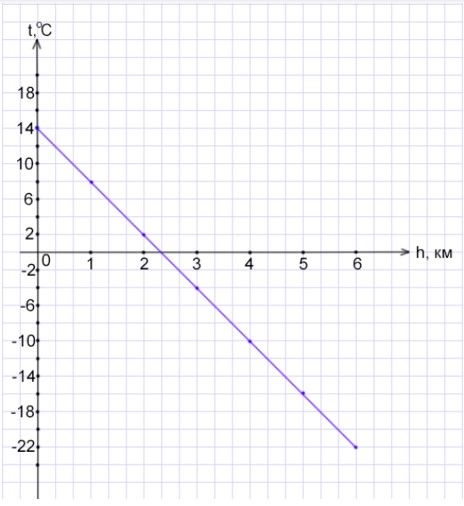
Номер 7.
Рассчитайте, сколько паркетной доски размером 1 м 60 см на 17 см надо купить, чтобы застелить пол в комнате размером 5,6 м на 3,6 м. Остатки доски меньше 40 см не использовать.
Ответ:1 м 60 см = 1,6 м
17 см = 0,17 м
1 вариант: по длине комнаты.
1) 5,6 : 1,6 = 56 : 16 = 3,5 (доски) – по длине;
0,5 доски – это 80 см (160 см ∙ 0,5 = 80 см) и она больше 40 см, значит её можно использовать.
2) 3,6 : 0,17 = 360 : 17 = 21 (ост. 3) ≈ 22 (доски) – по ширине;
3) 22 ∙ 3,5 = 77 (досок) – всего понадобиться.
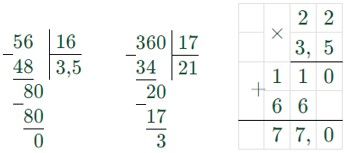
Второй вариант: по ширине комнате.
1) 3,6 : 1,6 = 36 : 16 = 2,25 (доски) – по ширине комнаты;
0,25 доски – это 40 см (160 см ∙ 0,25 = 40 см), значит её можно использовать.
2) 5,6 : 0,17 = 560 : 17 = 32 (ост. 16) ≈ 33 (доски) – по длине комнаты;
3) 33 ∙ 2,25 = 74,25 ≈ 75 (досок) – всего понадобится.
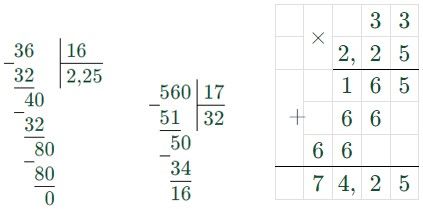
Второй вариант выгоднее.
Ответ: понадобится 75 досок.
Номер 8.
Экспертная лаборатория определяет рейтинг R фенов по показателям функциональности F, качеству Q и дизайну D на основе коэффициента ценности, равного 0,01 средней цены Р. Показатели оцениваются целым числом от 0 до 4. Рейтинг вычисляется по формуле: R = 4(2F + 2Q + D) – 0,01Р. Какая модель фенов, представленных в таблице, получит наивысший рейтинг?.

Рейтинг модели А:
R = 4 ∙ (2 ∙ 3 + 2 ∙ 1 + 3) - 0,01 ∙ 1580 = 4 ∙ (6 + 2 + 3) – 15,8 = 4 ∙ 11 – 15,8 = 44 – 15,8 = 28,2
Рейтинг модели Б:
R = 4 ∙ (2 ∙ 1 + 2 ∙ 2 + 2) - 0,01 ∙ 1610 = 4 ∙ 8 – 16,1 = 32 – 16,1 = 15,9
Рейтинг модели В:
R = 4 ∙ (2 ∙ 2 + 2 ∙ 3 + 1) - 0,01 ∙ 2150 = 4 ∙ 11 – 21,5 = 44 – 21,5 = 22,5
Рейтинг модели Г:
R = 4 ∙ (2 ∙ 0 + 2 ∙ 2 + 0) - 0,01 ∙ 1970 = 4 ∙ 4 – 19,7 = 16 – 19,7 = -3,7
Наивысший рейтинг у модели А.
Ответ: модель А.
Номер 9.
Длина рулона обоев равна 10 м, а его ширина – 0,5 м. Сколько нужно рулонов обоев под покраску для комнаты длиной 6,2 м, шириной 4,5 м и высотой 3 м, если площадь окон и дверей составляет 10 % общей площади?
Ответ:Обои – 10 м х 0,5 м - ? шт.
Длина – 6,2 м
Ширина – 4,5 м
Высота – 3 м
Площадь окон и дверей – 10% от общей площади
1) 2 ∙ (6,2 + 4,5) ∙ 3 = 2 ∙ 10,7 ∙ 3 = 21,4 ∙ 3 = 64,2 (м2) – общая площадь с окнами и дверьми;
2) 64,2 ∙ 0,1 = 6,42 (м2) – площадь окон и дверей;
3) 64,2 – 6,42 = 57,78 (м2) – площадь под обои;
4) 10 ∙ 0,5 = 5 (м2) – площадь 1 рулона;
5) 57,78 : 5 = 11,556 ≈ 12 (рулонов)
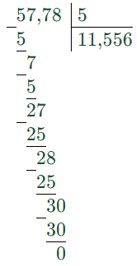
Ответ: 12 рулонов обоев нужно под покраску.
Номер 10.
Прочитайте внимательно текст и выполните задания 1−6.
Родители Юры и Светы решили на следующий год начать строительство нового дома в деревне, где живут их родители. Сначала они планируют залить ленточный фундамент из бетона для деревянного дома размером 8 х 12 м с одной внутренней перегородкой (рис. 6.41, а). Подземная часть фундамента планируется глубиной 0,9 м, а наземная часть высотой 0,40 м. Высота подушки гравия под фундамент должна составлять 15%, а песчаной 20 % от глубины подземной части фундамента (рис. 6.41, б). Стоимость кубометра гравия с доставкой 1900 р., а песка 7/20 от стоимости бетона.
Если траншею вырыть вручную, то залить бетон в траншею можно без опалубки. Для наземной части нужны опалубка из обрезной доски толщиной 25 мм и шириной 150 мм и крепёж для опалубки (рис. 6.41, в). Для столбиков крепежа в деревне есть арматура, а для крепежа сверху Юра распилит старые бруски.
Бетон можно заказать у трёх производителей.
Цена доставки бетона за кубометр у трёх поставщиков зависит от расстояния: до 10 км − 400 р., до 15 км − 450 р., до 20 км − 500 р. Цена кубометра бетона и дополнительные условия доставки бетона у трёх поставщиков приведены в таблице.
Осиновые доски длиной 6 м можно купить по цене от 10 тыс. р. за кубометр, а из хвои на 9 % дешевле, но осина хуже поддаётся гниению. Она практически не гниёт в воде и из неё делают лёгкие лодки. Бабушка планирует замену парников на следующий год, для них тоже потребуются доски. Доставка сосновых досок стоит 1400 р., а из осины − на 300 р. дешевле.
1. Определите объём фундамента.
2. Найдите, сколько кубометров песка потребуется для фундамента, и рассчитайте его стоимость.
3. Найдите, сколько кубометров гравия потребуется для фундамента, и рассчитайте его стоимость.
4. Найдите, сколько кубометров бетона потребуется для фундамента. Рассчитайте наиболее дешёвый вариант покупки бетона с доставкой на расстояние 15 км.
5. Найдите, сколько кубометров досок потребуется для фундамента. Определите стоимость покупки досок и решите, какие доски целесообразно приобрести.
6. Определите затраты на материалы для фундамента. Что можно исключить из затрат?
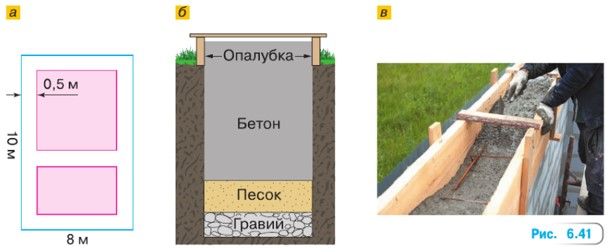
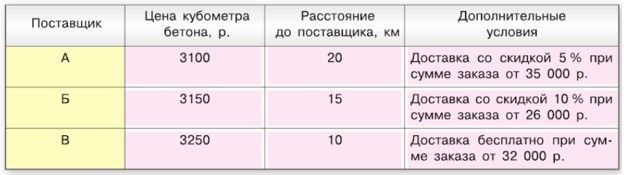
Пояснение: в условии задания говориться о доме с размером 8 х 12 м, а на рис. 6.41, а – с параметрами 8 х 10 м. Мы брали расчёты на дом 8 х 10 м, как на рисунке.
0,9 ∙ 15% = 0,9 ∙ 0,15 = 0,135 (м) – высота подушки гравия;
0,9 ∙ 20% = 0,9 ∙ 0,2 = 0,18 (м) – высота песчаной подложки;
(0,9 + 0,4) – (0,135 + 0,18) = 1,3 – 0,315 = 0,985 (м) – высота бетона.
1) 10 ∙ 0,5 ∙ 2 + 7 ∙ 0,5 ∙ 3 = 0,5 ∙ (20 + 21) = 0,5 ∙ 41 = 20,5 (м2) – площадь заливки бетона;
20,5 ∙ (0,9 + 0,4) = 20,5 ∙ 1,3 = 26,65 (м3) – объём фундамента.
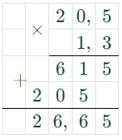
Ответ: 26,65 м3 объём фундамента.
2) 20,5 ∙ 0,18 = 3,69 (м3) – песка потребуется всего для фундамента;
Стоимость песка 7/20 от стоимости бетона.
Вариант А:
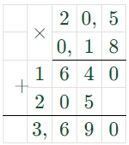
3100 ∙ 7/20 ∙ 3,69 = 3100 ∙ 0,35 ∙ 3,69 = 4003,65 (р.) – стоимость 3,69 м3 песка;
Вариант Б:
3150 ∙ 7/20 ∙ 3,69 = 3150 ∙ 0,35 ∙ 3,69 = 4068,225 ≈ 4068,23 (р.) – стоимость 3,69 м3 песка;
Вариант В:
3250 ∙ 7/20 ∙ 3,69 = 3250 ∙ 0,35 ∙ 3,69 = 4197,375 ≈ 4197,38 (р.) – стоимость 3,69 м3 песка.
Ответ: 3,69 м3 песка потребуется всего для фундамента; 4197,38 рубля стоимость песка.
3) 20,5 ∙ 0,135 = 2,7675 (м3) - гравия потребуется для фундамента;
Стоимость кубометра гравия с доставкой 1900 р.
2,7675 ∙ 1900 = 5258,25 (р.) – стоимость гравия.
Ответ: 2,7675 м3 гравия потребуется для фундамента; 5258,25 рубля стоимость гравия.
4) 20,5 ∙ 0,985 = 20,1925 (м3) – потребуется бетона;
На расстояние 15 км осуществляют доставку только поставщики А и Б.
Поставщик А: скидка на доставку 5%.
20,1925 ∙ (3100 + 450 ∙ (100% – 5%)) = 20,1925 ∙ (3100 + 450 ∙ 0,95) = 20,1925 ∙ (3100 + 427,5) = 20,1925 ∙ 3527,5 = 71 229,04375 ≈ 71 230 (р.) – стоимость бетона.
Поставщик Б: скидка на доставку 10%.
20,1925 ∙ (3150 + 450 ∙ (100% – 10%)) = 20,1925 ∙ (3150 + 450 ∙ 0,9) = 20,1925 ∙ (3150 + 405) = 20,1925 ∙ 3555 = 71 784,3375 ≈ 71 785 (р.) – стоимость бетона.
71 230 р. < 71 785 р.
Дешевле заказать у поставщика А.
Ответ: 20,1925 м3 потребуется бетона; 71 230 рублей – наиболее дешёвый вариант покупки бетона.
5) 2 ∙ (10 + 8 + 8,5 + 7 + 7) = 2 ∙ 40,5 = 81 (м) – периметр;
81 ∙ 3 = 243 (м) – длина досок.
Так как высота должна быть не менее 0,4 м, а ширина доски 0,15 м, то потребуется 3 доски в высоту (0,4 : 0,15 = 40 : 15 = 2 (ост. 10) ≈ 3).
243 : 6 = 40,5 ≈ 41 (доска) – необходимо для сооружения опалубки.
Так как длина одной доски 6 м.
6 ∙ 0,15 ∙ 0,025 = 0,9 ∙ 0,025 = 0,0225 (м3) – объём одной доски;
41 ∙ 0,0225 = 0,9225 (м3) – объём всех досок;
10 000 ∙ 0,9225 = 9225 (р.) - стоимость осиновых досок;
9225 + (1400 – 300) = 9225 + 1100 = 10 325 (р.) – стоимость осиновых досок с доставкой.
9225 ∙ (100% - 9%) = 9225 ∙ 0,91 = 8394,75 (р.) – стоимость хвойных досок;
8394,75 + 1400 = 9794,75 (р.) – стоимость хвойных досок с доставкой.
Целесообразно приобрести осиновые доски, так как они меньше гниют и если их заказать вместе с фундаментом, то можно сэкономить на доставке и тогда стоимость осиновых досок будет дешевле.
Ответ: 0,9225 м3 досок потребуется для фундамента; целесообразно приобрести осиновые доски по цене 10 325 рублей.
6) 4003,65 р. – стоимость песка;
5258,25 р. – стоимость гравия;
71 230 р. – стоимость бетона;
10 325 р. – стоимость осиновых досок с доставкой.
4003,65 + 5258,25 + 71 230 + 10 325 = 90 816,9 (р.) – затраты на материалы для фундамента.
Из затрат можно исключить доски на подземную часть фундамента.
Ответ: 90 816,9 рублей общие затраты на материал.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.