Математика 6 класс учебник Виленкин, Жохов 1 часть ответы – применяем математику на 116 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2023-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Применяем математику на странице 116
Номер 1.
Петя может покрасить забор за 8 ч, а Миша − за 10 ч. Успеют ли они покрасить весь забор до тренировки, которая начнётся через 5 ч?
Ответ:
Петя – за 8 ч
Миша – за 10 ч
Вместе за 5 ч – ? успеют
1) 1 ∶ 8 = 1/8 (часть) – забора покрасит Петя за 1 час;
2) 1 ∶ 10 = 1/10 (часть) – забора покрасит Миша за 1 час;
3) 1⁽⁵/8 + 1⁽⁴/10 = 5/40 + 4/40 = 9/40 (части) – забора покрасят мальчики вместе за 1 час;
4) 1 ∶ 9/40 = 1 · 40/9 = 40/9 = 4 4/9 (ч) – покрасят забор вместе;
4 4/9 ч < 5 ч – успеют покрасить.
Ответ: да, успеют они покрасить весь забор до тренировки.
Решение выражением:
1 ∶ (1⁽⁵/8 + 1⁽⁴/10) = 1 ∶ 9/40 = 40/9 = 4 4/9 (ч).
Номер 2.
1) Фарфор может состоять из 1 части полевого шпата, 3 частей кварца и 6 частей каолина (белая глина).
Найдите массу вазы, если в ней кварца на 0,24 кг больше, чем полевого шпата.
2) Сплавы магния используют в производстве ракет и авиационных турбин, корпусов приборов, дисков автомобильных колёс и др.
Их существует несколько видов. Часто сплав состоит из 1 части алюминия, 2 частей цинка и 18 частей магния.
Сколько получилось этого сплава, если в нём магния на 3,9 т больше, чем цинка?
Задача 1.
1-й способ решения:
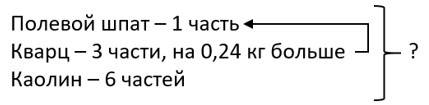
1) 3 − 1 = 2 (части) – на столько кварца больше, чем шпата или составляет 0,24 кг;
2) 0,24 : 2 = 0,12 (кг) – приходится на 1 часть;
3) 1 + 3 + 6 = 10 (частей) – приходится на вазу;
4) 0,12 · 10 = 1,2 (кг) – масса вазы.
Ответ: масса вазы 1,2 кг.
Решение выражением:
0,24 : (3 − 1) ∙ (1 + 3 + 6) = 0,24 : 2 ∙ 10 = 0,12 ∙ 10 = 1,2 (кг).
2-й способ решения:
Пусть в вазе х кг полевого шпата, тогда 3х кг – кварца и 6х кг – каолина.
Известно, что кварца на 0,24 кг больше, чем полевого шпата.
Составим уравнение:
3х − х = 0,24;
2х = 0,24;
х = 0,24 : 2;
х = 0,12.
0,12 кг – масса полевого шпата;
3х = 3 · 0,12 = 0,36 (кг) – масса кварца;
6х = 6 · 0,12 = 0,72 (кг) – масса каолина;
0,12 + 0,36 + 0,72 = 1,2 (кг) – масса вазы.
Ответ: масса вазы 1,2 кг.
Задача 2.
1-й способ решения:
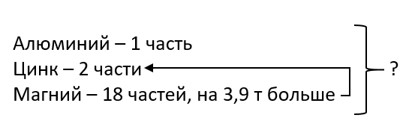
1) 18 − 2 = 16 (частей) – на столько магния больше, чем цинка или составляет 3,9 т; 2) 3,9 : 16 = 0,24375 (т) – приходится на 1 часть;

3) 1 + 2 + 18 = 21 (часть) – приходится на сплав; 4) 0,24375 · 21 = 5,11875 (т) – масса сплава.
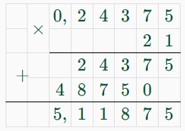
Ответ: получилось 5,11875 т сплава.
2-й способ решения:
Пусть в сплаве х т алюминия, тогда цинка – 2х т, а магния – 18х т.
Известно, что магния на 3,9 т больше, чем цинка.
Составим уравнение:
18х − 2х = 3,9;
16х = 3,9;
х = 3,9 : 16;
х = 0,24375.
0,24375 т – масса алюминия;
2х = 2 · 0,24375 = 0,4875 (т) – масса цинка;
18х = 18 · 0,24375 = 4,3875 (т) – масса магния;
0,24375 + 0,4875 + 4,3875 = 0,73125 + 4,3875 = 5,11875 (т) – масса сплава.
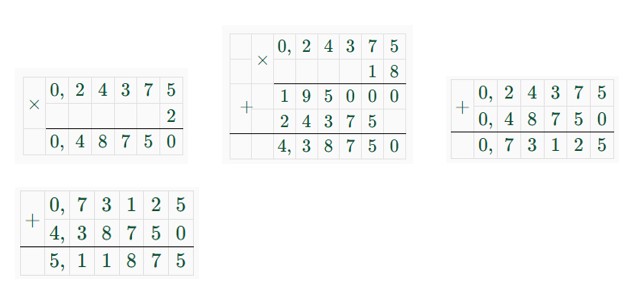
Ответ: получилось 5,11875 т сплава.
Номер 3.
Как разделить поровну семь дынь между 12 гостями, если каждую дыню можно разрезать только на равные части и частей должно быть не больше 5?
Ответ:
Четыре дыни нужно разделить на 3 равные части каждую и дать каждому по одной такой части.
Каждый получит по 1/3 части дыни.
Оставшиеся три дыни нужно разделить на 4 равные части каждую и каждому дать по одной части.
Каждый получит по 1/4 части дыни.
Каждый получит 1/3 дыни и 1/4 дыни.
Номер 4.
Который сейчас час, если оставшаяся часть суток в 1 2/5 раза больше прошедшей?
Ответ:
Пусть х ч – прошедшая часть суток, тогда 1 2/5 x ч – оставшаяся часть суток.
В сутках 24 часа.
Составим уравнение:
x + 1 2/5x = 24;
(1 + 1 2/5)x = 24;
2 2/5x = 24;
12/5x = 24;
x = 24 ∶ 12/5;
x = 24 · 5/12;
x = ²̶2̶4̶ · 5/̶1̶2̶ ₁;
x = 2 · 5;
x = 10.
10 ч – прошедшая часть суток.
Сейчас 10 часов утра.
Ответ: 10 часов утра.
Номер 5.
В небольшом городке 10 памятников архитектуры (рис. 2.14). Туристу хочется посетить их все, не проходя дважды по одной и той же улице. Может ли он это сделать?
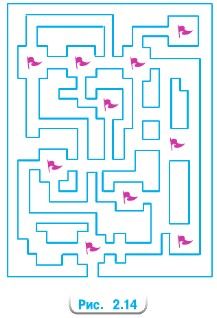
Турист может это сделать.
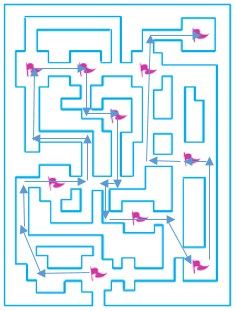
Номер 6.
В магазине продают два сорта конфет по цене 200 р. и 300 р. Стоимость конфет каждого сорта для приготовления ассорти одинакова. По какой цене надо продавать ассорти этих конфет, чтобы не обмануть покупателя и магазину не иметь убытка?
Ответ:
1 сорт – 200 р.
2 сорт – 300 р.
Ассорти – ? р.
1) НОК (200; 300) = 600
600 р. – стоимость конфет каждого вида;
2) 600 : 200 = 3 (кг) – конфет по цене 200 р.;
3) 600 : 300 = 2 (кг) – конфет по цене 300 р.;
4) 3 + 2 = 5 (кг) – всего конфет;
5) 200 · 3 + 300 · 2 = 600 + 600 = 1200 (р.) – стоимость всех конфет;
6) 1200 : 5 = 240 (р.) – стоимость ассорти.
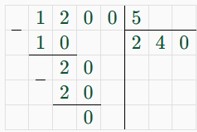
Ответ: смесь конфет нужно продавать по 240 рублей.
Номер 7.
По рецепту для приготовления трёх порций молочного коктейля требуется: 250 г молока, 8 столовых ложек мороженого и по 2 ложки или варенья, или мёда, или сиропа. Нужно приготовить коктейль для 8 гостей. Найдите массу каждого продукта для приготовления коктейля. Одна столовая ложка мороженого, варенья, мёда или сиропа содержит 15 г данного продукта.
Ответ: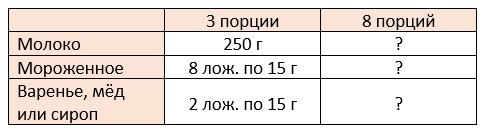
1) 250 ∶ 3 · 8 = 250 · 8/3 = 2000/3 = 666 2/3 (г) – молока нужно для 8 порций коктейля;
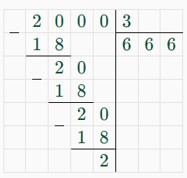
2) 8 · 15 : 3 · 8 = 120 : 3 · 8 = 40 · 8 = 320 (г) – мороженного нужно для 8 порций коктейля;
3) 2 · 15 : 3 · 8 = 30 : 3 · 8 = 10 · 8 = 80 (г) – варенья, мёда или сиропа нужно для 8 порций коктейля.
Ответ: 666 2/3 г молока; 320 г мороженного, 80 г варенья, мёда или сиропа.
Номер 8.
Участники благотворительного концерта передали 5,7 млн р. городу, пострадавшему после наводнения. На ремонт школ и детских садов было использовано 5/16 этой суммы, на отправку детей на отдых в другие регионы − 3/16 этой суммы, на ремонт больниц − в 2 раза больше, чем на отдых детей, оставшуюся сумму направили на ремонт стадиона. Сколько денег было направлено на ремонт стадиона и на отдых детей?
Ответ: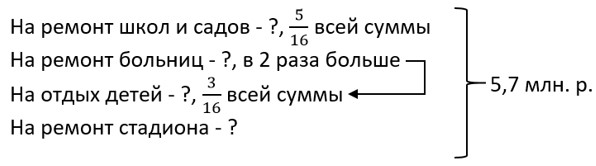
1) 3/16 · 2 = 6/16 = 3/8 (всей суммы) – на ремонт больниц; 2) 5/16 + 3/16 +3/8 = 8/16 + 3/8 = 4/8 + 3/8 = 7/8 (всей суммы) – на ремонт школ и садов, на ремонт больниц и на отдых детей вместе; 3) 1 − 7/8 = 8/8 − 7/8 = 1/8 (всей суммы) – на ремонт стадиона; 4) 5,7 · 3/16 = 57/10 · 3/16 = 171/160 = 1,06875 (млн. руб.) = 1 068 750 руб. – на отдых детей; 5) 5,7 · 1/8 = 57/10 · 1/8 = 57/80 = 0,7125 (млн. руб.) = 712 500 руб. – на ремонт стадиона.

Ответ: на ремонт стадиона было направлено 712 500 рублей и на отдых детей 1 068 750 рублей.
Номер 9.
Бандероли отправляются массой от 100 г до 2 кг. Какую наименьшую сумму потребуется заплатить за отправку в лагерь наборов карандашей и наборов красок для рисования 17 детям? Масса набора красок для рисования равна 2/5 кг, а масса набора карандашей — 1/40 кг. Тарифы на отправку бандероли приведены в таблице справа.
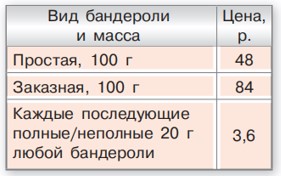
Масса красок – 2/5 кг
Масса карандашей – 1/40 кг
Количество наборов – 17 шт.
1) 2⁽⁸/5 + 1/40 = 16/40 + 1/40 = 17/40 (кг) – масса одного набора;
2) 17/40 · 17 = 289/40 = 7,225 (кг) = 7225 г – масса 17 наборов;
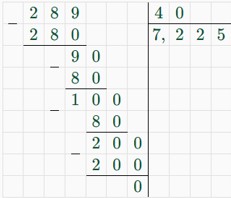
3) 7225 : 100 = 72,25 – в посылке содержится 72 раза по 100 г и еще 25 г; 4) 48 · 72 + 3,6 · 2 = 3456 + 7,2 = 3463,2 (р.) – наименьшая сумма.
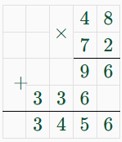
Ответ: 3463,2 рублей потребуется заплатить за отправку в лагерь наборов карандашей и наборов красок для рисования.
Номер 10.
Чтобы рассчитать расстояние до телевизора, нужно умножить диагональ телевизора на коэффициент 1,6. Измерьте диагональ вашего телевизора и найдите оптимальное расстояние для просмотра телепередач.
Ответ:
Возьмём диагональ телевизора – 1 м.
1 ∙ 1,6 = 1,6 (м) – расстояние для просмотра телепередач.
Ответ: 1,6 м оптимальное расстояние для просмотра телепередач.
Номер 11.
Задача Эйлера. Решив все свои сбережения поделить поровну между всеми сыновьями, некто составил завещание: "Старший из моих сыновей должен получить 1000 рублей и восьмую часть остатка; следующий − 2000 рублей и восьмую часть нового остатка; третий сын − 3000 рублей и восьмую часть следующего остатка и т.д." Определите число сыновей и размер завещанных сбережений.
Ответ:
Пусть х – размер завещанных сбережений, тогда первый сын получил 1000 р. и восьмую часть от остатка – это
1000 + 1/8 · (x − 1000) = 1000 + 1/8x − 1000/8 = 1000 − 125 + 1/8x = 875 + 1/8x.
Второй получит 2000 р. и восьмую часть нового остатка – это
2000 + 1/8 · (x − (875 + 1/8x) − 2000) = 2000 + 1⁽⁸/8x − 875/8 − 1/64x − 2000/8 = 2000 − 109 3/8 − 250 + 8/64x − 1/64x = 1640 5/8 + 7/64x
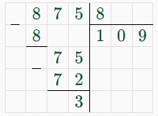
Известно, что между всеми сыновьями сбережения поделили поровну.
Составим уравнение:
875 + 1/8x = 1640 5/8 + 7/64x
1⁽⁸/8x − 7/64x = 1640 5/8 − 875
8/64x − 7/64x = 765 5/8
1/64x = 6125/8
x = 6125/8 : 1/64
x = 6125/8 · 64/1
x = 6125 · ̶6̶4̶⁸/̶8̶ ₁
x = 6125 · 8
x = 49 000
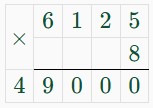
49 000 р. – размер завещанных сбережений. 875 + 1/8x = 875 + 1/8 · 49 000 = 875 + 49 000/8 = 875 + 6125 = 7000 (р.) – получит каждый сын. 49 000 : 7000 = 7 (сыновей) – число сыновей.

Ответ: 7 сыновей, 49 000р размер завещанных сбережений.
Номер 12.
Надпись на гробнице знаменитого древнего математика Диофанта составлена в виде математической задачи.
Путник! Здесь прах погребён Диофанта.
И числа поведать могут, о чудо, сколь долог был век его жизни.
Часть шестую его представляло прекрасное детство.
Двенадцатая часть протекла ещё жизни − покрылся пухом тогда подбородок.
Седьмую в бездетном браке провёл Диофант.
Прошло пятилетие; он был осчастливлен рожденьем прекрасного первенца сына.
Коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец восприял, переживши года четыре с тех пор, как сына лишился.
Скажи, сколько лет жизни достигнув, смерть восприял Диофант?
Пусть Диофант прожил х лет, тогда 1/6 x лет – детство, 1/12 x лет – юность, 1/7 x лет – в браке, 1/2 x лет – прожил сын, ещё 5 лет без детей и 4 года после смерти сына.
Составим уравнение:
1/6x + 1/12x + 1/7x + 1/2x + 5 + 4 = x
(1⁽¹⁴/6 + 1⁽⁷/12 + 1⁽¹²/7 + 1⁽⁴²/2) · x + 9 = x
(14/84 + 7/84 + 12/84 + 42/84) · x + 9 = x
75/84x + 9 = x
x − 75/84x = 9
(84/84 − 75/84) · x = 9
9/84x = 9
x = 9 ∶ 9/84
x = 9 · 84/9
x = ̶9̶ · 84/̶9̶
x = 84
84 года – прожил Диофант.
Ответ: Диофант прожил 84 года.
Номер 13.
Известному писателю Л. Н. Толстому очень нравилась следующая задача. Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще остался участок, скошенный на другой день косцом за один день работы. Сколько косцов было в артели?
Ответ:
1-й способ решения:
В первый день скосили большое поле и часть малого с остатком которго справился один на второй день.
3х/(х + 4) = 2
3х = 2(х + 4)
3х = 2х + 8
3х − 2х = 8
х = 8 (косцы)
Ответ: 8 косцов было в артели.
2-й способ решения:
По условию большой луг полдня косила вся артель и полдня пол-артели, значит все косцы за первые полдня скосили 2/3 большого участка, а за вторые полдня пол-артели 1/3 этого же участка.
На втором участке, равном половине первого, за вторую половину дня также скосили 1/3.
И к вечеру на малом лугу остался нескошенным участок в 1/2 − 1/3 = 1/6, который скосил один косец.
Получается, что один косец в день скашивает 1/6 луга, а скошено было 6/6 + 2/6 = 8/6, значит косцов было 8.
Ответ: 8 косцов.
Номер 14.
Задача Л. Ф. Магницкого. Некий человек нанял работника на год, обещал ему дати 12 рублёв и кафтан. Но тот, работав 7 месяцев, восхотел уйти, и просил достойной платы с кафтаном. Хозяин дал ему по достоинству расчёт 5 рублей и кафтан, и ведательно есть, а коликие цены оный кафтан был.
Ответ:
1-й способ решения:
Пусть х р. стоит кафтан, тогда (12 + х) р. - это зарплата за год.
Следовательно ((12 + х) : 12) р. – зарплата за месяц, а за 7 месяцев – ((12 + х) : 12 · 7) (р.) и это по условию равно 5 рублей и кафтан или (5 + х) р.
Составим уравнение:
(12 + x) ∶ 12 · 7 = 5 + x
(12/12 + x/12) · 7 = 5 + x
1 · 7 + x/12 · 7 = 5 + x
7 + 7/12x = 5 + x
x − 7/12x = 7 − 5
(12/12 − 7/12)x = 2
5/12x = 2
x = 2 ∶ 5/12
x = 2 · 12/5
x = 24/5
x = 4,8
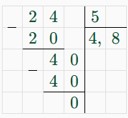
4,8 р. – стоимость кафтана.
Ответ: 4,8 рублёв цена кафтана.
2-й способ решения:
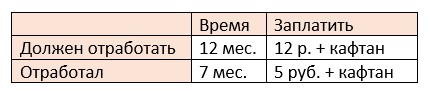
1) 12 − 7 = 5 (мес.) – не доработал работник до года;
2) 12 − 5 = 7 (р.) – не дополучил работник за 5 месяцев;
3) 7 : 5 = 1,4 (р.) – оплата за месяц;
4) 1,4 · 7 = 9,8 (р.) – должен получить работник за 7 месяцев;
5) 9,8 − 5 = 4,8 (р.) – цена кафтана.
Ответ: 4,8 рублёв цена кафтана.
Номер 15.
К табунщику пришли три казака покупать лошадей. "Хорошо, я вам продам лошадей, − сказал табунщик, − первому продам я полтабуна и ещё половину лошади, второму − половину оставшихся лошадей и ещё пол-лошади, третий также получит половину оставшихся лошадей с полулошадью. Себе же оставлю только 5 лошадей". Удивились казаки, как это табунщик будет делить на части. Но после некоторых размышлений они успокоились, и сделка состоялась. Сколько лошадей продал табунщик каждому из казаков?
Ответ:
Казак 1 – ?, 1/2 табуна + 1/2 лошади
Казак 2 – ?, 1/2 остатка + 1/2 лошади
Казак 3 – ?, 1/2 остатка + 1/2 лошади
Осталось – 5 лошадей
1) 5 + 1/2 = 5 1/2 (лошади) – половина остатка после продажи второму казаку;
2) 5 1/2 · 2 = 5,5 · 2 = 11 (лошадей) – остаток после продажи второму казаку;
3) 11 − 5 = 6 (лошадей) – продали третьему казаку;
4) 11 + 1/2 = 11 1/2 (лошадей) – половина остатка после продажи первому казаку;
5) 11 1/2 · 2 = 11,5 · 2 = 23 (лошади) – остаток после продажи первому казаку;
6) 23 − 11 = 12 (лошадей) – продали второму казаку;
7) 23 + 1/2 = 23 1/2 (лошадей) – половина табуна;
8) 23 1/2 · 2 = 23,5 · 2 = 47 (лошадей) – табун;
9) 47 − 23 = 24 (лошади) – продали первому казаку.
Ответ: табунщик продал первому казаку 24 лошади, второму − 12 лошадей и третьему − 6 лошадей.
Номер 16.
Длина маршрутной тропы на гору Малое Седло в Кисловодске равна 5,4 км. Подняться на гору можно разными способами:
1) пройти по тропе пешком;
2) подняться в вагончике канатной дороги, который едет 1/16 ч. Затем пройти оставшиеся 2 км.
Рассчитайте время различных вариантов похода, если обычно средняя скорость восхождения на гору составляет 1,5 км/ч, а спуска − в два с половиной раза больше.
При этом не забудьте добавить время на то, чтобы поесть, полюбоваться чудесными видами природы и отдохнуть.
1-й вариант похода (пешком)

1) 5,4 : 1,5 = 54 : 15 = 3,6 (ч) – время подъёма на гору пешком; 2) 1,5 · 2,5 = 3,75 (км/ч) – скорость спуска с горы пешком; 3) 5,4 : 3,75 = 540 : 375 = 1,44 (ч) – время спуска с горы пешком;

4) 3,6 + 1,44 = 5,04 (ч) – время на поход пешком без отдыха.
5) Время на поесть – 1 час;
Время на полюбоваться природой – 1 час;
5,04 + 1 + 1 = 7,04 ≈ 7 (ч) – время на поход пешком с учётом отдыха.
Ответ: примерно 7 часов.
2-й вариант похода (в вагончике)

1) 1/16 + 1/16 = 2/16 = 1/8 (ч) – время движения по канатной дороге;
2) 2 ∶ 1,5 = 20 ∶ 15 = 20/15 = 4/3 = 1 1/3 (ч) – время подъёма 2 км пешком;
3) 2 ∶ 3,75 = 200 ∶ 375 = 200/375 = 8/15 (ч) – время спуска 2 км пешком;
4) 1⁽¹⁵/8 + 1 1⁽⁴⁰/3 + 8⁽⁸/15 = 15/120 + 1 40/120 + 64/120 = 1 119/120 (ч) ≈ 2 (ч) – время похода на гору в вагончике канатной дороги без отдыха;
5) Время на поесть – 1 час;
Время на полюбоваться природой – 1 час;
2 + 1 + 1 = 4 (ч) – время похода на гору в вагончике канатной дороги с отдыхом.
Ответ: примерно 4 часа.
Вывод: подняться в вагончике канатной дороге на гору быстрее, чем идти пешком.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.