Математика 6 класс учебник Виленкин, Жохов 1 часть ответы – номер 2.118

Тип: ГДЗ, Решебник.
Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
Часть: 1.
Год: 2023-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Еремина

Номер 2.118.

Развивай мышление.

а) Найдите в таблице простых чисел пары чисел-близнецов среди первых 500 натуральных чисел. Сколько таких пар получилось? б) Все пары чисел-близнецов, кроме 3 и 5, имеют вид 6n – 1 или 6n + 1. Найдите по этим выражениям пары чисел для n, равного 87, 135 и 165. в) Не все пары чисел вида 6k – 1 и 6k + 1 являются числами-близнецами. Найдите все пары двузначных чисел вида 6k – 1 и 6k + 1, которые не являются числами-близнецами.

Ответ:

а) (3, 5); (5, 7); (11, 13); (17, 19); (29, 31); (41, 43); (59, 61); (71, 73); (101, 103); (107, 109); (137, 139); (149, 151); (179, 181); (191, 193); (197, 199); (227, 229); (239, 241); (269, 271); (281, 283); (311, 313); (347, 349); (419, 421); (431, 433); (461, 463) – 24 пары.
б) Если n = 87, то 6n – 1 = 6 · 87 – 1 = 522 – 1 = 521 – простое число. 6n + 1 = 6 · 87 + 1 = 522 + 1 = 523 – простое число.

математика 6 класс Виленкин, Жохов - 1 часть Номер 2.118

Ответ: числа 521 и 523 взаимно простые.
Если n = 135, то 6n – 1 = 6 · 135 – 1 = 810 – 1 = 809 – простое число. 6n + 1 = 6 · 135 + 1 = 810 + 1 = 811 – простое число.

математика 6 класс Виленкин, Жохов - 1 часть Номер 2.118-1

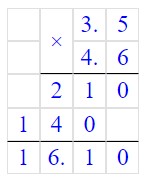
Ответ: числа 809 и 811 взаимно простые.
Если n = 165, то 6n – 1 = 6 · 165 – 1 = 990 – 1 = 989 – составное число. 6n + 1 = 6 · 165 + 1 = 990 + 1 = 991 – простое число.

математика 6 класс Виленкин, Жохов - 1 часть Номер 2.118-2

    НОД (989, 991) = 1.
Ответ: числа 989 и 991 взаимно простые.
в) При n = 4,     6n – 1 = 6 · 4 – 1 = 24 – 1 = 23 – простое число;     6n + 1 = 6 · 4 + 1 = 24 + 1 = 25 – составное число.     Числа 23 и 25 не являются числами-близнецами.
    При n = 6,     6n – 1 = 6 · 6 – 1 = 36 – 1 = 35 – составное число;     6n + 1 = 6 · 6 + 1 = 36 + 1 = 37 – простое число.     Числа 35 и 37 не являются числами-близнецами.
    При n = 8,     6n – 1 = 6 · 8 – 1 = 48 – 1 = 47 – простое число;     6n + 1 = 6 · 8 + 1 = 48 + 1 = 49 – составное число.     Числа 47 и 49 не являются числами-близнецами.
    При n = 9,     6n – 1 = 6 · 9 – 1 = 54 – 1 = 53 – простое число;     6n + 1 = 6 · 9 + 1 = 54 + 1 = 55 – составное число.     Числа 53 и 55 не являются числами-близнецами.
    При n = 11,     6n – 1 = 6 · 11 – 1 = 66 – 1 = 65 – составное число.     6n + 1 = 6 · 11 + 1 = 66 + 1 = 67 – простое число.     Числа 65 и 67 не являются числами-близнецами.
    При n = 13,     6n – 1 = 6 · 13 – 1 = 78 – 1 = 77 – составное число;     6n + 1 = 6 · 13 + 1 = 78 + 1 = 79 – простое число.     Числа 77 и 79 не являются числами-близнецами.
    При n = 14,     6n – 1 = 6 · 14 – 1 = 84 – 1 = 83 – простое число;     6n + 1 = 6 · 14 + 1 = 84 + 1 = 85 – составное число.     Числа 83 и 85 не являются числами-близнецами.
    При n = 15,     6n – 1 = 6 · 15 – 1 = 90 – 1 = 89 – простое число.     6n + 1 = 6 · 15 + 1 = 90 + 1 = 91 – составное число.     Числа 89 и 91 не являются числами-близнецами.
    При n = 16,     6n – 1 = 6 · 16 – 1 = 96 – 1 = 95 – составное число.     6n + 1 = 6 · 16 + 1 = 96 + 1 = 97 – простое число.     Числа 95 и 97 не являются числами-близнецами.
Ответ: (23, 25); (35, 37); (47, 49); (53, 55); (65, 67); (77, 79); (83, 85); (89, 91); (95, 97) – не являются числами-близнецами.