Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 85-86 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Проверьте себя
Проверочная работа "Действие умножения. Свойство умножения"
Проверочная работа № 1.
1. Увеличьте число пятнадцать в четыре раза.
2. Увеличьте число шестнадцать на четыре.
3. Найдите произведение двадцати и шести.
4. Чему равно произведение, если множители равны четырём и двадцати пяти?
5. Замените сумму 50 + 50 + 50 + 50 произведением и вычислите его значение.
Запишите выражение:
6. Произведение «игрек» и тридцати восьми.
7. Какое число больше «эм» на пятнадцать?
8. Какое число больше «икс» в шестнадцать раз?
1. 15 · 4 = 60
2. 16 + 4 = 20
3. 20 · 6 = 120
4. 4 · 25 = 100
5. 50 + 50 + 50 + 50 = 50 · 4 = 200
6. 38у
7. m + 15
8. 16х
Проверочная работа № 2.
Запишите выражение для решения задачи:
1. В домашней библиотеке у Марины двести пятьдесят книг, а в школьной библиотеке в тридцать пять раз больше книг. Сколько книг в школьной библиотеке?
2. За один час поезд проходит шестьдесят пять километров. Какое расстояние пройдёт поезд за восемь часов?
3. В одной коробке «икс» электрических лампочек. Сколько лампочек в двадцати трёх таких коробках?
4. Разложите на два равных множителя число шестьдесят четыре.
5. Найдите произведение, если множители равны четырём и двумстам пятидесяти.
Верно ли высказывание (ответьте да или нет)?
6. В произведении 54 · m второе слагаемое — «эм».
7. Выражение 19 · (х – 74) читают так: «произведение девятнадцати и разности «икс» и семидесяти четырёх».
8. Произведение трёхсот восьмидесяти девяти и нуля равно трёмстам восьмидесяти девяти.
1. 250 · 35
2. 65 · 8
3. 23х
4. 64 = 8 · 8
5. 4 · 250 = 1 000
6. Нет.
7. Да.
8. Нет.
Словарный диктант.
Запишите математические термины:
1. Ра...н...сть
2. Сл...жен...
3. Множ...т...ль
4. Выч...тан...
5. Зн...чен... выр...жен...
6. Ур...внен...
7. Выч...та...м...е
8. Ед...ница
1. Разность.
2. Сложение.
3. Множитель.
4. Вычитание.
5. Значение выражения.
6. Уравнение.
7. Вычитаемое.
8. Единица.
Проверьте себя
Проверочная работа № 1.
1. Найдите произведение 18 и 9.
2. Найдите произведение суммы 18 и 9 и разности 18 и 9.
3. Разложите на множители число 162 двумя способами.
4. Сравните произведения:
а) 14 ∙ 15 и 15 ∙ 14;
б) 2 ∙ 3 ∙ 4 ∙ 5 и 6 ∙ 21;
в) 3 ∙ (4 + 12) и (4 + 8) ∙ 4;
г) 7х и 0 ∙ х .
5. Не вычисляя, сравните значения выражений:
а) 23 ∙ 46 и 38 ∙ 23;
б) 438 ∙ 198 и 605 ∙ 198.
1. 18 ∙ 9 = 162.
2. (18 + 9) ∙ (18 – 9) = 27 ∙ 9 = 243.
3. 162 = 2 ∙ 81 и 162 = 3 ∙ 54.
4. а) 14 ∙ 15 = 15 ∙ 14.
б) 2 ∙ 3 ∙ 4 ∙ 5 < 6 ∙ 21, так как 2 ∙ 3 ∙ 4 ∙ 5 = 6 ∙ 20.
в) 3 ∙ (4 + 12) = (4 + 8) ∙ 4, так как
3 ∙ (4 + 12) = 3 ∙ 16 = 48;
(4 + 8) ∙ 4 = 12 ∙ 4 = 48.
г) 7х > 0 ∙ х.
5. а) 23 ∙ 46 > 38 ∙ 23;
б) 438 ∙ 198 < 605 ∙ 198.
Номер 1.
Чтобы найти произведение двух чисел нужно первый множитель умножить на второй множитель.18 ∙ 9 = (20 – 2) · 9 = 20 · 9 – 2 · 9 = 180 – 18 = 162.
Ответ: проведение чисел 18 и 9 равно 162.
Номер 2.
1) Найдём сумму чисел 18 и 9, для этого к числу 18 прибавим число 9.18 + 9 = 27 – сумма чисел 18 и 9.
2) Найдём разность чисел 18 и 9, для этого из числа 18 вычтем число 9.
18 – 9 = 9 – разность чисел 18 и 9.
3) Найдём произведение суммы и разности чисел 18 и 9, для этого результат, который получился в пункте 1 умножим на результат пункта 2.
27 · 9 = 27 · (10 – 1) = 270 – 27 = 243 – произведение суммы и разности чисел 18 и 9.
Оформим это в виде выражения:
(18 + 9) ∙ (18 – 9) = 27 ∙ 9 = (20 + 7) · 9 = 20 · 9 + 7 · 9 = 180 + 63 = 243.
Ответ: произведение суммы 18 и 9 и разности 18 и 9 равна 243.
Номер 3.
Разложим число 162 на простые множители: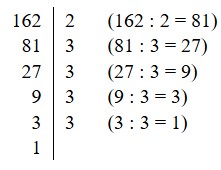
Число 162 можно разложить на множители несколькими способами.
Выберите 2 способа из данных:
162 = 2 ∙ 81;
162 = 3 ∙ 54;
162 = 6 · 27;
162 = 9 · 18.
Номер 4.
а) 14 ∙ 15 = 15 ∙ 14.Вспомним переместительное свойство умножения: от перемены мест множителей проведение не меняется.
б) 1) Рассмотрим первое выражение: 2 · 3 · 4 · 5 = 6 · 20.
2) Сравним первое выражение со вторым выражением:
6 · 20 < 6 · 21, так как 20 < 21 и 6 = 6.
Вспомним, что произведение тем больше, чем больше множители в нём.
Значит, 2 ∙ 3 ∙ 4 ∙ 5 < 6 ∙ 21.
в) 1) Найдём значение первого выражения: 3 · (4 + 12) = 12 + 36 = 48.
2) Найдём значение второго выражения: (4 + 8) ∙ 4 = 12 ∙ 4 = 48.
3) Сравним полученные значения: 48 = 48.
Значит, 3 · (4 + 12) = (4 + 8) · 4.
г) Рассмотрим два случая:
Первый случай: Если х = 0, то 7х = 0 · х
Проверим, подставив х = 0 в выражения:
7х = 7 · 0 = 0 и 0 · х = 0 · 0 = 0, тогда 0 = 0.
Второй случай: Если х ≠ 0, то 7х > 0 ∙ х, так как 0 · х = 0, а 7х > 0.
Номер 5.
Вспомним, что произведение тем больше, чем больше множители в нём.а) 23 ∙ 46 > 38 ∙ 23, так как 23 = 23, а 46 > 38.
б) 438 ∙ 198 < 605 ∙ 198, так как 198 = 198, а 438 < 605.
Проверочная работа № 2.
1. На детском дне рождения было заказано 6 корзиночек с клубникой по 120 р., 12 безе по 82 р., 8 шоколадных пирожных по 105 р., 6 чашей чая по 54 р. и 6 стаканов сока по 70 р.
а) Сколько заплатили за корзиночки с клубникой?
б) Сколько заплатили за безе?
в) Сколько заплатили за пирожные?
г) Сколько заплатили за напитки?
д) На сколько больше заплатили за пирожные, чем за напитки?
е) Сколько стоил весь заказ?
2. Вычислите удобным способом:
а) 8 ∙ 125 ∙ 34;
б) 25 ∙ 760 ∙ 4;
в) 20 ∙ 53 ∙ 50;
г) 800 ∙ 25 ∙ 8.
3. Найдите произведение:
а) 40 ∙ 81;
б) 12 ∙ 90;
в) 106 ∙ 410;
г) 210 ∙ 301.
4. Найдите корень уравнения:
а) 34 – (х – 7) = 18;
б) (х + 24) – 15 = 12;
в) (56 – х) + 34 = 72;
г) 62 + (15 + х) = 148.
5. Составьте выражение по условию задачи:
Водитель легкового автомобиля заехал заправиться на бензоколонку. Объём бака его машины равен 50 л. Сколько будет стоить водителю заправить полный бак своего автомобиля, если 1 л бензина стоит:
а) х = 47 р.;
б) х = 52 р.?
1. а) 120 ∙ 6 = 720 (р.) – за корзиночки с клубникой;
б) 82 ∙ 12 = 984 (р.) – за безе;
в) 105 ∙ 8 = 840 (р.) – за пирожные;
г) 54 ∙ 6 + 70 ∙ 6 = 324 + 420 = 744 (р.) – за напитки;
д) 840 – 744 = 96 (р.) – на сколько больше заплатили за пирожные, чем за напитки;
е) 720 + 984 + 840 + 744 = 3288 (р.) – весь заказ.
2. а) 8 ∙ 125 ∙ 34 = 1000 ∙ 34 = 34 000;
б) 25 ∙ 760 ∙ 4 = (25 ∙ 4) ∙ 760 = 100 ∙ 760 = 76 000;
в) 20 ∙ 53 ∙ 50 = (20 ∙ 50) ∙ 53 = 1000 ∙ 53 = 53 000;
г) 800 ∙ 25 ∙ 8 = 800 ∙ 200 = 160 000.
3. а) 40 ∙ 81 = 3240;
б) 12 ∙ 90 = 1080;
в) 106 ∙ 410 = 43 460;
г) 210 ∙ 301 = 63 210.

4. а) 34 – (х – 7) = 18
х – 7 = 34 – 18
х – 7 = 16
х = 16 + 7
х = 23
Ответ: 23.
б) (х + 24) – 15 = 12
х + 24 = 12 + 15
х + 24 = 27
х = 27 – 24
х = 3
Ответ: 3.
в) (56 – х) + 34 = 72
56 – х = 72 – 34
56 – х = 38
х = 56 – 38
х = 18
Ответ: 18.
г) 62 + (15 + х) = 148
15 + х = 148 – 62
15 + х = 86
х = 86 – 15
х = 71
Ответ: 71.
5. 50 ∙ х
а) Если х = 47р., то 50 ∙ х = 50 ∙ 47 = 2350 (р.)
б) Если х = 52 р., то 50 ∙ х = 50 ∙ 52 = 2600 (р.)
Номер 1.
Составим краткую запись задачи:Корзинки с клубникой – 6 шт. по 120 р.
Безе – 12 шт. по 82 р.
Шок. пирожных – 8 шт. по 105 р.
Чая – 6 ч. по 54 р.
Сок – 6 ст. по 70 р.
Вспомним, чтобы найти стоимость, нужно цену умножить на количество.
а) Корзинки с клубникой стоят 120 рублей и таких купили 6 корзинок.
120 · 6 = (100 + 20) · 6 = 600 + 120 = 720 (р.) – заплатили за корзиночки с клубникой.
б) Купили 12 безе по 82 рубля каждая, значит:
82 · 12 = 82 · (10 + 2) = 820 + 164 = 984 (р.) – заплатили за безе.
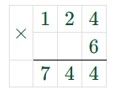
в) Шоколадных пирожных купили 8 штук по 105 рублей каждое, значит:
105 · 8 = 800 + 40 = 840 (р.) – заплатили за пирожные.
г) 1) Чая купили 6 чашек по 54 рубля, значит:
54 · 6 = (50 + 4) · 6 = 300 + 24 = 324 (р.) – заплатили за 6 чашек чая;
2) Стакан сока стоит 70 рублей и таких купили 6 стаканов.
70 · 6 = 420 (р.) – заплатили за 6 стаканов сока;
3) Сложим общую стоимость чая и сока и узнаем сколько заплатили за напитки.
324 + 420 = 744 (р.) – всего заплатили за напитки.
Стоимость всех напитков можно вычислить выражением:
54 · 6 + 70 · 6 = (54 + 70) · 6 = 124 · 6 = 744 (р.) – заплатили за напитки.
д) За пирожные заплатили 840 рублей, а за напитки – 744 рубля.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
840 - 744 = 96 (р.) – на столько больше заплатили за пирожные, чем за напитки.
е) Сложим стоимость вех покупок и узнаем общую стоимость заказа.
720 + 984 + 840 + 744 = 1560 + 1728 = 3288 (р.) – заплатили за весь заказ.
Номер 2.
Чтобы вычислить наиболее удобным способом, будем применять переместительное и сочетательное свойства умножения.а) 8 ∙ 125 ∙ 34 = (8 · 125) · 34 = 1000 ∙ 34 = 34 000;
б) 25 ∙ 760 ∙ 4 = (25 ∙ 4) ∙ 760 = 100 ∙ 760 = 76 000;
в) 20 ∙ 53 ∙ 50 = (20 ∙ 50) ∙ 53 = 1000 ∙ 53 = 53 000;
г) 800 ∙ 25 ∙ 8 = 800 · 25 · (4 · 2) = (800 · 2) · (25 · 4) = 1600 · 100 = 160 000.
Номер 3.
Для удобства вычисления будем применять распределительное свойство умножения.а) 40 ∙ 81 = 40 · (80 + 1) = 40 · 80 + 40 · 1 = 3200 + 40 = 3240.
Разложим число 80 на сумму чисел 80 и 1. Каждое слагаемое умножим на число 40, а потом полученные произведения сложим.
б) 12 ∙ 90 = (10 + 2) · 90 = 10 · 90 + 2 · 90 = 900 + 180 = 1080.
Разложим число 12 на сумму чисел 10 и 2. Каждое слагаемое умножим на число 90, а потом полученные произведения сложим.
в) 106 ∙ 410 = (100 + 6) · 410 = 100 · 410 + 6 · 410 = 41 000 + 2460 = 43 460.
Разложим число 106 на сумму чисел 100 и 6. Каждое слагаемое умножим на число 410, а потом полученные произведения сложим.
г) 210 ∙ 301 = 210 · (300 + 1) = 210 · 300 + 210 · 1 = 63 000 + 210 = 63 210.
Разложим число 301 на сумму чисел 300 и 1. Каждое слагаемое умножим на число 210, а потом полученные произведения сложим.
Номер 4.
При решении уравнений вначале находим значение выражения в скобках, а затем находим неизвестную переменную, которая была в скобках.а) 34 – (х – 7) = 18;
Найдём неизвестное вычитаемое (х – 7):
х – 7 = 34 – 18;
х – 7 = 16;
Теперь найдём неизвестное уменьшаемое х:
х = 16 + 7;
х = 23.
Ответ: х = 23.
Сделаем проверку:
34 – (23 – 7) = 34 – 23 + 7 = 11 + 7 = 18;
18 = 18 – верно.
б) (х + 24) – 15 = 12;
Найдём неизвестное уменьшаемое (х + 24):
х + 24 = 12 + 15;
х + 24 = 27;
Теперь найдём неизвестное слагаемое х:
х = 27 – 24;
х = 3.
Ответ: х = 3.
Сделаем проверку:
(3 + 24) – 15 = 27 – 15 = 12;
12 = 12 – верно.
в) (56 – х) + 34 = 72;
Найдём неизвестное слагаемое (56 – х):
56 – х = 72 – 34;
56 – х = 38;
Теперь найдём неизвестное вычитаемое х:
х = 56 – 38;
х = 18.
Ответ: х = 18.
Сделаем проверку:
(56 – 18) + 34 = 38 + 34 = 72;
72 = 72 – верно.
г) 62 + (15 + х) = 148;
Найдём неизвестное слагаемое (15 + х):
15 + х = 148 – 62;
15 + х = 86;
Теперь найдём неизвестное слагаемое х:
х = 86 – 15;
х = 71.
Ответ: х = 71.
Сделаем проверку:
62 + (15 + 71) = 62 + 86 = 148;
148 = 148 – верно.
Номер 5.
Пусть х – стоимость 1 литра бензина. Объём бака машины равен 50 литров.Чтобы узнать стоимость бензина, для заполнения полного бака, нужно объём бака машины умножить на стоимость 1 литра бензина, значит:
(50 ∙ х) р. – стоимость заправки полного бака.
Чтобы найти значение буквенного выражения, нужно вместо переменной буквы подставить соответствующее ей число и выполнить вычисления.
а) Если х = 47 р., то
50 ∙ х = 50 ∙ 47 = 50 · (40 + 7) = 50 · 40 + 50 · 7 = 2000 + 350 = 2350 (р.) – стоимость заправки полного бака, если литр бензина стоит 47 рублей.
б) Если х = 52 р., то
50 ∙ х = 50 ∙ 52 = 50 · (50 + 2) = 2500 + 100 = 2600 (р.) – стоимость заправки полного бака, если литр бензина стоит 52 рубля.
Ответ: заправить полный бак стоит а) 2350 рублей; б) 2600 рублей.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.