Запишите выражение:
1. Сумма пятнадцати и двадцати пяти.
2. Разность восьмидесяти девяти и тридцати.
3. Сумма сорока и «икс».
4. Разность «эм» и ста трёх.
5. Сумма «икс» и «игрек».
6*. Разность «эн» и выражения «икс» плюс восемь».
Верно ли высказывание (ответьте да или нет)?
7. Выражение 9 + (d – 5) называется суммой.
8. Выражение (m + 4) – 7 называется разностью.
1. 15 + 25
2. 89 – 30
3. 40 + х
4. m – 103
5. x + y
6. n – (x + 8)
7. Да.
9. Да.
Запишите выражение:
1. Разность «ка» и выражения «эм» плюс одиннадцать».
2. Сумма выражения «пять минус «игрек» и «икс».
3*. Разность выражения «восемь минус «эн» и выражения «икс» плюс двадцать».
Запишите выражение для решения задачи:
4. У Пети «икс» тетрадей, а у Иры шесть тетрадей. Сколько тетрадей у них вместе?
5. Серёжа съел «эм» конфет, а Витя — на «эн» конфет меньше. Сколько конфет съел Витя?
6*. Брату «икс» лет, и он на три года старше сестры. Сколько лет сестре?
Верно ли высказывание (ответьте да или нет)?
7. В выражении 18 + (y – 9) разность «игрек» и девяти является слагаемым.
8. В выражении (x + 7) – 15 сумма «икс» и семи является вычитаемым.
1. k – (m + 11)
2. (5 – y) + x
3. (8 – n) – (x + 20)
4. x + 6
5. m – n
6. x – 3
7. Да.
8. Нет.
Запишите выражение и упростите его:
1. Разность пятидесяти и выражения «эм» плюс пятнадцать».
2. Разность выражения «тридцать шесть плюс «икс» и двадцати.
3. Сумма двадцати восьми и выражения «эн» плюс сорок».
4. Сумма шестидесяти, «икс» и пятидесяти.
5. Разность семидесяти и выражения «тридцать плюс «икс».
Верно ли высказывание (ответьте да или нет)?
6. После упрощения выражения a – 20 + 45 получится сумма «а» и пятнадцати.
7. В выражении (16 – k) + 14 разность шестнадцати и «ка» является уменьшаемым.
8. Разность двух чисел не изменится, если из уменьшаемого и из вычитаемого вычесть одно и то же число.
1. 50 – (m + 15) = 50 – 15 – m = 35 – m
2. (36 + x) – 20 = 36 – 20 + x = 16 + x
3. 28 + (n + 40) = (28 + 40) + n = 68 + n
4. 60 + x + 50 = x + 60 + 50 = x + 110
5. 70 – (30 + x) = 70 – 30 – x = 40 – x
6. Нет.
7. Да.
8. Да.
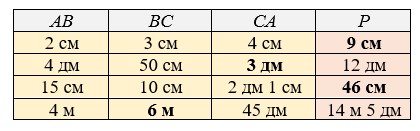
1. Составьте выражение для вычисления периметра P треугольника ABC. Найдите недостающие значения в таблице:
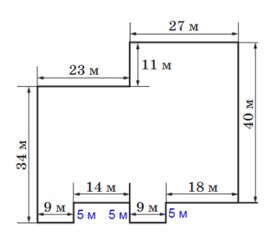
2* На рисунке 2.17 изображён план пруда.
Составьте числовое выражение для вычисления периметра пруда. Найдите значение этого выражения.
1. Р = АВ + ВС + СА.
2. 23 м + 11 м + 27 м + 40 м + 18 м + 5 м + 9 м + 5 м + 14 м + 5 м + 9 м + 34 м = 200 м – периметр.
1. Запишите сумму:
а) 100 – 45 и 200 + 30;
б) а + 10 и 100;
в) x + 15 и y – 8;
г) p – 25 и s + 30.
2. Запишите выражение: сумма t и 326 уменьшена на 309.
а) Какой задаче соответствует составленное выражение?
1. Купили две книги. Цена одной книги меньше цены другой книги на 326 р. Сколько заплатили за покупку, если была скидка 309 р.?
2. Две книги вместе стоили (t – 326) р. Сколько стоит первая книга, если вторая книга стоит 309 р.?
б) Упростите составленное выражение и найдите его значение при t = 390; 1798.
3. Запишите разность:
а) 200 + 30 и 100 – 45;
б) 100 и а +10;
в) x + 15 и y – 8;
г) s + 30 и p – 25.
4. Найдите значение выражения:
а) а + b – 1023 при a = 210, b = 4032;
б) 6230 – (x + y) при x = 195, y = 3457;
в) 4500 – 2с при с = 56.
1. а) (100 – 45) + (200 + 30);
б) (а + 10) + 100;
в) (x + 15) + (y – 8);
г) (p – 25) + (s + 30).
2. (t + 326) – 309
а) 1. (t + (t – 326)) – 309 – не соответствует;
2. (t – 326) – 309 – не соответствует.
б) (t + 326) – 309 = t + (326 – 309) = t + 17;
Если t = 390, то 390 + 17 = 407;
Если t = 1798, то 1798 + 17 = 1815.
3. а) (200 + 30) – (100 – 45);
б) 100 – (а +10);
в) (x + 15) – (y – 8);
г) (s + 30) – (p – 25).
4. а) а + b – 1023;
Если a = 210, b = 4032, то 210 + 4032 – 1023 = 4242 – 1023 = 3219.
б) 6230 – (x + y);
Если x = 195, y = 3457, то 6230 – (195 + 3457) = 6230 – 3652 = 2578.
в) 4500 – 2с;
Если с = 56, то 4500 – 2 ∙ 56 = 4500 – 112 = 4388.
Напишите свой комментарий внизу страницы.