Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 154-155 странице

Учебник 1 часть. Математика 5 класс. Учебник Виленкин.

Тип: ГДЗ, Решебник.
Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
Часть: 1.
Год: 2020-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Еремина

Отличается задание? Переключите год учебника.

2021 2023

Проверьте себя

Проверочная работа "Объёмы. Объёмы прямоугольного параллелепипеда"

Проверочная работа № 1.

1. Фигура составлена из ста семидесяти кубиков с ребром один сантиметр. Чему равен объём этой фигуры?
Выразите в кубических сантиметрах:
2. Пятнадцать кубических дециметров.
3. Тридцать тысяч кубических миллиметров.
Выразите в литрах:
4. Двенадцать кубических метров.
5. Четыре тысячи кубических сантиметров.
Верно ли высказывание (ответьте да или нет)?
6* Объём фигуры в двести тысяч кубических миллиметров больше одного кубического дециметра.
7. Литр — это объём куба с ребром один дециметр.
8. В бочку объёмом один кубический метр можно налить одну тысячу сто литров воды.

Ответ:

1. V = 170 см³
2. 15 дм³ = 15 000 см³
3. 30 000 мм³ = 30 см³
4. 12 м³ = 12 000 дм³ = 12 000 л
5. 4 000 см³ = 4 дм³ = 4 л

6. Нет.
200 000 мм³ = 200 см³ и 1 дм³ = 1 000 см³
200 см³ < 1 000 см³

7. Да.

8. Нет.
1 м³ = 1 000 дм³ = 1000 л 1000 л < 1100 л

Проверочная работа № 2.

1. Измерения прямоугольного параллелепипеда равны двум, пяти и шести дециметрам. Найдите его объём.
2. Измерения прямоугольного параллелепипед равны пятнадцати сантиметрам, одному дециметру и двум дециметрам. Найдите его объём.
3. Ребро куба равно двум дециметрам. Найдите его объём.
4. Ребро куба равно трём сантиметрам. Найдите его объём.
5. Объём комнаты равен шестидесяти кубическим метрам, а площадь пола — двадцати квадратным метрам. Найдите высоту комнаты.
6* Чему равно ребро куба, объём которого равен ста двадцати пяти литрам?
Верно ли высказывание (ответьте да или нет)?
7. Объём куба, площадь поверхности которого шесть квадратных дециметров, равен одному литру.
8. В бак, размеры которого пятьдесят сантиметров, двадцать сантиметров и двадцать пять сантиметров, можно налить сорок литров воды.

Ответ:

1. V = 2 · 5 · 6 = 10 · 6 = 60 дм³

2. 1 дм = 10 см, 2 дм = 20 см
V = 15 · 10 · 20 = 10 · 300 = 3000 см³ = 3 дм³

3. V = 2 · 2 · 2 = 2³ = 8 дм³
4. V = 3 · 3 · 3 = 3³ = 27 см³

5. c = V : S
c = 60 : 20 = 3 м

6. 125 л = 125 дм³ = 5 дм · 5 дм · 5 дм
Ребро куба равно 5 дм.

7. Да.
6 дм² = 600 см²
S = 6а²
а² = 600 : 6 = 100 = 10 · 10
a = 10 см – ребро куба
V = 10 · 10 · 10 = 1000 см³ = 1 дм³ = 1 л

8. Нет.
V = 50 · 20 · 25 = 1000 · 25 = 25 000 см³ = 25 дм³ = 25 л
25 л < 40 л

Словарный диктант.

Запишите математические термины:
1. П...рим...т...
2. Об...ём
3. Пр...м...угол...ный
4. Д...ц...мет...
5. Ку...ич...ский
6. Пло...д...
7. Ку...
8. П...р...л...л...п...п...

Ответ:

1. Периметр.
2. Объём.
3. Прямоугольный.
4. Дециметр.
5. Кубический.
6. Площадь.
7. Куб.
8. Параллелепипед.

Проверьте себя

Проверочная работа № 1.

1. Выразите:
а) 20 дм³ в литрах, в кубических сантиметрах.
б) 5 л в кубических дециметрах, в кубических сантиметрах.
в) 25 000 см³ в кубических дециметрах, в литрах.

2. Найдите объем прямоугольного параллелепипеда с измерениями 10 см, 2 дм и 1 м.

3. Найдите высоту прямоугольного параллелепипеда объемом 3960 мм³ и площадью основания 120 мм².

4. Найдите площадь основания прямоугольного параллелепипеда объемом 1716 л и высотой 110 см.

5. Площадь поверхности куба равна 96 см². Найдите, чему равен объем.

Ответ:

1. а) 20 дм³ = 20 л = 20 000 см³
б) 5 л = 5 дм³ = 5000 см³
в) 25 000 см³ = 25 дм³ = 25 л

2. 2 дм = 20 см;
1 м = 100 см;
10 ∙ 20 ∙ 100 = 20 000 (см³) = 20 (дм³) – объём.

3. 3960 : 120 = 33 (мм) – высота.

4. 1716 л = 1716 дм³ = 1 716 000 см³
1 716 000 : 110 = 15 600 (см²) – площадь основания.

5. 1) 96 : 6 = 16 (см) – площадь одной грани куба;
2) 16 = 4 * 4, значит, сторона куба равна 4 см;
3) 4 ∙ 4 ∙ 4 = 16 ∙ 4 = 64 (см³) – объём куба.

Номер 1.

Вспомним, что 1 дм³ = 1 л и 1 дм³ = 1000 см³.

а) 20 дм³ = 20 л;
20 дм³ = (20 · 1000) = 20 000 см³.

б) 5 л = 5 дм³;
5 л = (5 · 1000) = 5000 см³.

в) 25 000 см³ = (25 000 : 1000) = 25 дм³;
25 000 см³ = 25 л.

Номер 2.

Объём прямоугольного параллелепипеда равен произведению трёх его измерений – длины, ширины и высоты.
При вычислении объёма все измерения сторон должны быть представлены в одинаковых единицах измерениях.

Выразим все измерения прямоугольного параллелепипеда в см:
а = 10 см
b = 2 дм = 20 см
c = 1 м = 100 см
V – ?

Найдём объём прямоугольного параллелепипеда, учитывая, что 1000 см³ = 1 дм³.
10 ∙ 20 ∙ 100 = 20 000 (см³) = (20 000 : 1000) = 20 (дм³) – объём прямоугольного параллелепипеда.

Ответ: объём равен 20 дм³.

Номер 3.

Составим краткую запись:
V = 3960 мм³
S = 120 мм²
c – ?

Объём прямоугольного параллелепипеда можно найти если площадь основания умножить на высоту.
Значит, чтобы найти высоту можно площадь основания разделить на объём прямоугольного параллелепипеда.
3960 : 120 = 33 (мм) = 3 см 3 мм – высота.

Пояснение к проверочной работе страница 154-155

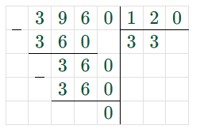
Ответ: высота равна 33 мм или 3 см 3 мм.

Номер 4.

Составим краткую запись:

V = 1716
c = 110 см
S_осн – ?

1) Выразим объём прямоугольного параллелепипеда в см³.
Будем учитывать, что 1 л = 1 дм³ и 1 дм³ = 1000 см³.
1716 л = 1716 дм³ = (1716 · 1000) = 1 716 000 см³ – объём прямоугольного параллелепипеда.

2) Объём прямоугольного параллелепипеда можно найти если площадь основания умножить на высоту.
Значит, чтобы найти площадь основания можно объём прямоугольного параллелепипеда разделить на его высоту.
Будем учитывать, что 1 дм² = 100 см².
1 716 000 : 110 = 15 600 (см²) = (15 600 : 100) = 156 см² – площадь основания.

Ответ: площадь основания равна 156 дм².

Номер 5.

Составим краткую запись:

S_{пов. куба} = 96 см²
V_куба – ?

1) Куб состоит из 6 равных граней. Площадь поверхности куба равна сумме площадей всех его граней.
Значит, чтобы найти площадь одно грани куба нужно площадь поверхности куба разделить на 6 (количество граней).
96 : 6 = (60 + 36) : 6 = 10 + 6 = 16 (см²) – площадь одной грани куба;

2) Каждая грань куба имеет форму квадрата и её площадь равна 16 см².
Площадь квадрата равна квадрату его стороны. Следовательно, если площадь квадрата равна 16 см2, то есть сторона равна 4 см, так как 4² = 4 · 4 = 16.
4 см – ребро (сторона) куба.

3) У куба все рёбра равны, значит, чтобы найти объём куба нужно его сторону возвести в куб.
4³ = 4 ∙ 4 ∙ 4 = 16 ∙ 4 = 64 (см³) – объём куба.

Ответ: объём куба равен 64 см³.

Проверочная работа № 2.

1. Используя таблицу:
а) найдите объем первого прямоугольного параллелепипеда;
б) выразите высоту второго прямоугольного параллелепипеда в дециметрах;
в) найдите площади каждой грани третьего параллелепипеда;
г) выясните, может ли поместиться: первый прямоугольный параллелепипед внутри второго; второй прямоугольный параллелепипед внутри третьего.

2. Во сколько раз объем куба с ребром 2 дм меньше объема куба с ребром 2 м?

3. Выразите в кубических метрах и дециметрах:
а) 4 265 000 см³;
б) 1200 дм³.

Математика 5 класс учебник Виленкин 1 часть. Страница 154-155, проверочная работа, номер 1. Год 2023.

Ответ:

1. а) 5 дм = 50 см
20 ∙ 8 ∙ 50 = 8000 (см³) = 8 (дм³) – объём первого параллелепипеда;

б) 60 : (5 ∙ 2) = 60 : 10 = 6 (м) = 60 (дм) – высота второго прямоугольного параллелепипеда;

в) 18 м³ = 18 000 дм³;
50 см = 5 дм;
20 м = 200 дм.
1) 18 000 : (200 ∙ 5) = 18 000 : 1000 = 18 (дм) – длина третьего параллелепипеда;
2) 18 ∙ 200 = 3600 (дм²);
3) 18 ∙ 5 = 90 (дм²);
4) 200 ∙ 5 = 1000 (дм²).

Ответ: 3600 дм²; 90 дм²; 1000 дм².

г) Первый прямоугольный параллелепипед может поместиться внутри второго.
Второй прямоугольный параллелепипед не может поместиться внутри третьего.

2.
1) 2 дм ∙ 2 дм ∙ 2 дм = 8 (дм³) – объём куба с ребром 2 дм;
2) 2 м ∙ 2 м ∙ 2 м = 8 (м³) = 8000 (дм³) – объём куба с ребром 2 м;
3) 8000 : 8 = 1000 (раз) - во сколько раз объем куба с ребром 2 дм меньше объема куба с ребром 2 м.

Ответ: в 1000 раз.

3. а) 4 265 000 см³ = 4 м³ 265 дм³
б) 1200 дм³ = 1 м³ 200 дм³

Номер 1.

а) Объём прямоугольного параллелепипеда равен произведению трёх его измерений – длины, ширины и высоты.
Найдём объём первого прямоугольного параллелепипеда с измерениями 20 см, 8 см и 5 дм = 50 см.
Учитываем, что 1 дм³ = 1000 см³.
20 ∙ 8 ∙ 50 = 8000 (см³) = (8000 : 1000) = 8 (дм³) – объём первого прямоугольного параллелепипеда.

Ответ: объём первого параллелепипеда равен 8 дм³.

б) Чтобы найти высоту прямоугольного параллелепипеда можно его объём разделить на произведение длины и ширины.
Найдём высоту второго прямоугольного параллелепипеда, если его объём равен 60 м³, длина – 5 м, а ширина – 2 м.
Учитываем, что 1 м = 10 дм.
60 : (5 ∙ 2) = 60 : 10 = 6 (м) = 60 (дм) – высота второго прямоугольного параллелепипеда.

Ответ: высота второго параллелепипеда равна 60 дм.

в) Вначале найдём длину третьего прямоугольного параллелепипеда.
Чтобы найти длину прямоугольного параллелепипеда можно его объём разделить на произведение ширины и высоты.
Для удобства вычисления выразим все измерения в дм:
Объём – 18 м³ = 18 000 дм³
Ширина – 20 м = 200 дм
Высота – 50 см = 5 дм

1) 18 000 : (200 ∙ 5) = 18 000 : 1000 = 18 (дм) – длина третьего параллелепипеда.

Третий параллелепипед состоит из сторон 18 дм, 200 дм и 5 дм. Площади противоположных граней равны.
Грани – это прямоугольники, в котором противоположные стороны равны.
Чтобы найти площадь прямоугольника нужно умножить его две различные стороны.
2) 18 ∙ 200 = 3600 (дм²) – площадь каждой из двух граней с размерами 18 х 200 дм;
3) 18 ∙ 5 = 90 (дм²) – площадь каждой из двух граней с размерами 18 х 5 дм;
4) 200 ∙ 5 = 1000 (дм²) – площадь каждой из двух граней с размерами 200 х 5 дм.

Ответ: площади граней равны 3600 дм²; 90 дм²; 1000 дм².

г) Сравним измерения первого и второго прямоугольного параллелепипеда:
20 см < 5 м, так как 20 см = 2 дм;
8 см < 2 м, так как 2 м = 20 см;
5 дм < 60 дм.
Длина, ширина и высота первого параллелепипеда меньше, чем измерения у второго.
Значит, первый прямоугольный параллелепипед может поместиться внутри второго.

Сравним объёмы второго и третьего прямоугольного параллелепипеда:
60 м³ > 18 м³
Объём второго параллелепипеда больше объёма третьего параллелепипеда, значит второй прямоугольный параллелепипед не может поместиться внутри третьего.

Ответ: первый параллелепипед может поместиться внутри второго; второй параллелепипед не может поместиться внутри третьего.

Заполним таблицу найденными значениями:

Номер 2.

Составим краткую запись в виде таблицы: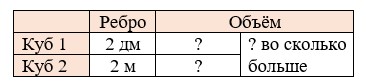

Найдём объём каждого куба. У куба все рёбра равны, значит, чтобы найти объём куба нужно его сторону возвести в куб.
Также вспомним, что 1 м³ = 1000 дм³.
1) 2³ = 2 ∙ 2 ∙ 2 = 8 (дм³) – объём куба с ребром 2 дм;
2) 2³ = 2 ∙ 2 ∙ 2 = 8 (м³) = (8 · 1000) = 8000 (дм³) – объём куба с ребром 2 м.

3) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее:
8000 : 8 = 1000 (раз) – объём куба с ребром 2 дм меньше, чем объём куба с ребром 2 м.

Ответ: объём куба с ребром 2 дм меньше, чем объём куба с ребром 2 м в 1000 раз.

Номер 3.

Вспомним, что 1 дм = 10 см, значит 1 дм³ = 1000 см³;
1 м = 10 дм, значит 1 м³ = 1000 дм³.

а) 4 265 000 см³ = (4 265 000 : 1000) дм³ = 4265 дм³ = 4000 дм³ + 265 дм³ = (4000 : 1000) м³ + 265 дм³ = 4 м³ 265 дм³;
б) 1200 дм³ = 1000 дм³ + 200 дм³ = 1 м³ 200 дм³.

Конец страницы