Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 146 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Проверьте себя
Проверочная работа "Единицы измерения площадей"
Выразите в квадратных метрах:
1. Восемнадцать аров.
2.Двадцать тысяч квадратных дециметров.
Выразите в гектарах:
3. Двенадцать квадратных километров.
4. Три тысячи аров.
Верно ли высказывание (ответьте да или нет)?
5. Шесть тысяч квадратных метров равны шестидесяти соткам.
6*. Площадь прямоугольного участка со сторонами сто тридцать метров и девяносто метров больше одного гектара.
7. На участке площадью сорок аров один гектар отвели под огород.
8. Площадь квадратного участка со стороной девять метров меньше одного ара.
1. 18 а = 1800 м2
2. 20 000 дм2 = 200 м2
3. 12 км2 = 120 000 га
4. 3 000 а = 30 га
5. Да, верно.
6000 м2 = 60 соток
6. Да, верно.
130 · 90 = 11 700 м2 = 1 га 1700 м2
7. Нет.
Так как 1 га = 100 а
8. Да, верно.
9 · 9 = 81 м2
1 а = 100 м2
Словарный диктант.
Запишите математические термины:
1. П...рим...т...
2. М...л...мет...
3. Пр...м...угол...ник
4. Пло...д...
5. Г...ктар
6. Тр...угол...ник
7. Кв...дра...
8. Д...ц...мет...
1. Периметр.
2. Миллиметр.
3. Прямоугольник.
4. Площадь.
5. Гектар.
6. Треугольник.
7. Квадрат.
8. Дециметр.
Проверьте себя
Проверочная работа.
1. Выпишите номера верных утверждений:
1) 1 га = 10 000 м2;
2) 400 а = 4 га;
3) 5 а < 500 дм2;
4) 20 м2 > 10 000 см2.
2. Выпишите номера неверных утверждений:
1) площадь участка со сторонами 30 м и 50 м равна 15 а;
2) площадь участка со сторонами 300 м и 50 м равна 15 а;
3) площадь участка со сторонами 300 м и 500 м равна 15 га.
3. Длина прямоугольника 25 м. При какой ширине прямоугольника его площадь:
а) будет равна 1 а;
б) будет больше 1 а;
в) будет меньше 1 а?
4. Найдите значение выражения:
а) 2 ∙ 33 + 4 ∙ 24;
б) (33 — 24)2.
1. 1; 2; 4.
2. 2.
3. а) 1 а : 25 м = 100 м2 : 25 м = 4 м;
б) больше 4 м;
в) меньше 4 м.
4. а) 2 ∙ 33 + 4 ∙ 24 = 2 ∙ 27 + 4 ∙ 16 = 54 + 64 = 118;
б) (33 — 24)2 = (27 – 16)2 = 112 = 121.
Номер 1.
1) Вспомним, что 1 га = 100 а, а 1а = 100 м2, значит1 га = (100 · 100) = 10 000 м2 – верно.
2) Вспомним, что 1 га = 100 а, значит
400 а = (400 : 100) = 4 га – верно.
3) Вспомним, что 1 а = 100 м2, а 1 м2 = 100 дм2, тогда
5 а = (5 · 100 · 100) = 50 000 дм2.
Сравним: 50 000 дм2 > 500 дм2.
Значит, 5 а < 500 дм2 – неверно.
4) Вспомним, что 1 м2 = 10 000 см2.
Сравним: 20 000 см2 > 10 000 см2.
Значит, 20 м2 > 10 000 см2 – верно.
Верные утверждения: 1, 2, 4.
Номер 2.
Вспомним, что площадь прямоугольника равна произведению длины и ширины.Также учитываем, что 1 а = 100 м2 и 1 га = 10 000 м2.
1) Вычислим площадь участка со сторонами 30 м и 50 м.
30 м · 50 м = 1500 м2 = (1500 : 100) = 15 а.
Значит, площадь участка со сторонами 30 м и 50 м равна 15 а – верно.
2) Вычислим площадь участка со сторонами 300 м и 50 м.
300 м · 50 м = 15 000 м2 = (15 000 : 100) = 150 а.
Значит, площадь участка со сторонами 300 м и 50 м равна 15 а – неверно.
3) Вычислим площадь участка со сторонами 300 м и 500 м.
300 м · 500 м = 150 000 м2 = (150 000 : 10 000) = 15 га.
Значит, площадь участка со сторонами 300 м и 500 м равна 15 га – верно.
Неверные утверждения: 2.
Номер 3.
Оформим краткую запись в виде таблицы: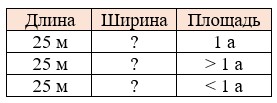
Площадь прямоугольника равна произведению длины и ширины.
Тогда, чтобы найти ширину нужно площадь разделить на длину.
Вспомним, что 1 а = 100 м2.
100 м2 : 25 м = 4 м – ширина прямоугольника.
а) площадь прямоугольника равна 1 а, если его ширина равна 4 м.
б) площадь прямоугольника больше 1 а, если его ширина больше 4 м.
в) площадь прямоугольника меньше 1 а, если его ширина больше 0 м, но меньше 4 м.
Номер 4.
Выполним вычисления по действиям:Разберём пример под а): 2 ∙ 33 + 4 ∙ 24 = 118.
1) Вначале возведём числа в степени:
33 = 3 · 3 · 3 = 9 · 3 = 27;
24 = 2 · 2 · 2 · 2 = 4 · 4 = 16.
2) Теперь выполним умножения:
2 · 27 = 2 · (20 + 7) = 40 + 14 = 54;
4 · 16 = 4 · (10 + 6) = 40 + 24 = 64.
3) Сложим полученные произведения:
54 + 64 = 118.
Разберём пример под б): (33 - 24)2 = 121.
1) Вначале возведём числа, находящиеся в скобках, в степени:
33 = 3 · 3 · 3 = 9 · 3 = 27;
24 = 2 · 2 · 2 · 2 = 4 · 4 = 16.
2) Найдём разность полученных чисел:
27 – 16 = 11.
3) Возведём полученное число в квадрат:
112 = 11 · 11 = 11 · (10 + 1) = 110 + 11 = 121.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.