Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 129 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Проверьте себя
Проверочная работа "Признаки делимости на 10, на 5 и на 2 / на 9 и на 3"
Проверочная работа № 1.
1. Запишите число, кратное пяти, которое на координатном луче расположено между семьюдесятью шестью и восемьюдесятью двумя.
2. Какой цифрой оканчивается чётное число, кратное пяти?
3. Какие цифры можно подставить вместо звёздочки в запись числа 5627*, чтобы это число делилось на пять?
4. Запишите нечётные числа, которые больше трёхсот пятидесяти и меньше трёхсот пятидесяти семи.
Верно ли высказывание (ответьте да или нет)?
5. Если число делится без остатка на десять, то оно не кратно двум.
6. Натуральное число «бэ» делится без остатка на пятнадцать. Значит, число «бэ» — делитель пятнадцати.
7. На координатном луче наименьшее кратное натурального числа «эн», не равное самому числу «эн», расположено правее этого числа на расстоянии «эн» единичных отрезков.
8. Если число кратно десяти, то оно делится и на два, и на пять.
1. 80
2. На 0
3. 0 или 5
4. 351, 353, 355
5. Нет.
6. Да.
7. Да.
8. Да.
Проверочная работа № 2.
1. Используя только цифру два, запишите наименьшее число, кратное трём.
2. Какую цифру можно подставить вместо звёздочки в запись числа 641*2, чтобы это число делилось на девять?
3. Запишите общий делитель двадцати одного и пятидесяти одного.
4. Какую цифру можно подставить вместо звёздочки в запись числа 973*, чтобы это число не было кратно трём?
Верно ли высказывание (ответьте да или нет)?
5. Если число кратно девяти, то оно делится без остатка на три.
6. Если девять — последняя цифра в записи натурального числа, то это число делится без остатка на девять.
7. Разность двух нечётных чисел — число нечётное.
8. Натуральное число, записанное двенадцатью одинаковыми цифрами, кратно трём.
1. 222
2. 5
3. Общий делитель – 3
4. 0, 1, 3, 4, 6, 7 или 9
5. Да.
6. Нет.
7. Нет.
8. Да.
Проверьте себя
Проверочная работа № 1.
1. Выберите из чисел 2, 5, 6, 10, 18, 180, 291, 2323, 3450, 15 555, 20 605, 33 333, 333 333 числа, которые:
а) делятся на 2;
б) делятся на 10;
в) не делятся на 2;
г) делятся на 5, но не делятся на 10;
д) кратны 9;
е) делятся на 3, но не делятся на 9;
ж) делятся на 2 и на 3.
2. Можно ли найти число, которое делится на 10, но не делится на 2?
3. На столе лежат рисунки, которых больше 60, но меньше 80. Эти рисунки можно сложить в папки по 6 либо по 8 рисунков. Сколько рисунков на столе?
4. Вычислите: (26 ∙ 652 – 16 ∙ 652) : 5 + 504 ∙ 4 : 9.
1. а) 2, 6, 10, 18, 180, 3450 – делятся на 2;
б) 10, 180, 3450 – делятся на 10;
в) 5, 291, 2323, 15 555, 20 605, 33 333, 333 333 – не делятся на 2;
г) 5, 15 555, 20 605 – делятся на 5, но не на 10;
д) 18, 180, 333 333 – кратны 9;
е) 6, 291, 3450, 15 555, 33 333 – делятся на 3, но не на 9;
ж) 6, 18, 180, 3450 – делятся на 2 и на 3.
2. Нет.
3. 72 рисунка на столе, так как число 72 делится и на 6 и на 8.
4. (26 ∙ 652 – 16 ∙ 652) : 5 + 504 ∙ 4 : 9 = 1528.
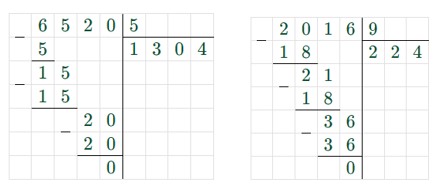
1) 26 ∙ 652 – 16 ∙ 652 = 652 ∙ (26 – 16) = 652 ∙ 10 = 6520;
2) 6520 : 5 = 1304;
3) 504 ∙ 4 = 2016;
4) 2016 : 9 = 224;
5) 1304 + 224 = 1528.
Номер 1.
Даны числа: 2, 5, 6, 10, 18, 180, 291, 2323, 3450, 15 555, 20 605, 33 333, 333 333.а) Числа, которые делятся на 2, называют чётными. Если число оканчивается чётной цифрой (0, 2, 4, 6, 8), то оно делится на 2.
Числа, которые делятся на 2:
2, 6, 10, 18, 180, 3450.
б) Число делится на 10, если оно оканчивается цифрой 0.
Числа, которые делятся на 10:
10, 180, 3450.
в) Числа, которые не делятся на 2, называют нечётными. Число, которое оканчивается нечетной цифрой (1, 3, 5, 7, 9), не делится на 2.
Числа, которые не делятся на 2:
5, 291, 2323, 15 555, 20 605, 33 333, 333 333.
г) Число, которое делится на 5, но не делятся на 10 должно оканчиваться цифрой 5.
Числа, которые делятся на 5, но не на 10:
5, 15 555, 20 605.
д) Число делится на 9 или кратно 9, если сумма цифр этого числа делится на 9.
Числа кратны 9:
18, 180, 333 333.
1 + 8 = 9 – кратно 9;
1 + 8 + 0 = 9 – кратно 9;
3 + 3 + 3 + 3 + 3 + 3 = 18 – кратно 9.
е) Числа, которые делятся на 3, но не на 9, это числа, у которых сумма цифр числа делится на 3, но не на 9.
Числа, которые делятся на 3, но не на 9:
6, 291, 3450, 15 555, 33 333.
ж) Числа, которые делятся на 2 и на 3 – это чётные числа, у которых сумма цифр числа делятся на 3.
Числа, которые делятся на 2 и на 3:
6, 18, 180, 3450.
Номер 2.
Не существует такого числа, которое бы делилось на 10 и не делилось бы на 2, так как на 10 делится любое число, которое оканчивается цифрой 0, а 0 – это чётная цифра, соответственно такое число будет чётное и оно будет делиться на 2.Ответ: такого числа найти нельзя.
Номер 3.
По условию рисунки можно сложить в папки по 6 либо по 8 рисунков, значит количество рисунков должно быть кратным 6 и 8 (то есть делиться на 6 и на 8). Также рисунков больше 60, но меньше 80.Значит это число 72, так как 60 < 72 < 80 и 72 – кратно 6 и 8.
72 : 6 = 12 и 72 : 8 = 9.
Ответ: число 72.
Номер 4.
(26 ∙ 652 – 16 ∙ 652) : 5 + 504 ∙ 4 : 9 = 1528.1) Вначале выполним вычисления в скобках: применяем распределительное свойство умножения. Общий множитель 652 вынесем за скобку.
В скобках останется разность чисел 26 и 16, выполни её.
Теперь умножим множитель 652 на полученную разность и получим 6520.
26 ∙ 652 – 16 ∙ 652 = 652 ∙ (26 – 16) = 652 ∙ 10 = 6520.
Дальше выполним по действиям:
2) 6520 : 5 = 1304;
3) 504 ∙ 4 = (500 + 4) · 4 = 2000 + 16 = 2016;
4) 2016 : 9 = 224;
5) 1304 + 224 = 1528.
Проверочная работа № 2.
1. Можно ли 234 человека рассадить в 5 автобусов поровну?
2. Запишите все делители числа 60.
3. Известно, что двухзначное число делится на 9 и состоит из одинаковых цифр. Выпишите все такие числа.
4. Известно, что нечётное трёхзначное число делится на 5 и состоит из цифр 0, 5, 7. Что это за число?
5. Катя купила 9 тетрадей и потратила на покупку 357 р. Могло ли такое быть, если цена тетради выражается натуральным числом рублей?
6. Не вычисляя суммы, установите, делиться ли на 3 каждое из слагаемых и будет ли делиться нацело на 3 их сумма:
а) 321 + 459;
б) 323 + 4571.
7. В числе 345* вместо звёздочки поставьте цифру так, чтобы полученное число:
а) делилось на 5;
б) делилось на 3 и на 9;
в) делилось на 2, на 3, на 5 и на 10.
1. Нет, так как число 234 не делится на 5 нацело.
2. 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
3. 99.
4. 705.
5. Нет, так как 357 не делится на 9 нацело.
6. а) 321 и 459 делятся на 3, значит и сумма делится на 3;
б) 323 и 4571 не делятся на 3, их сумма тоже не делится на 3.
7. а) 3455 или 3450;
б) 3456;
в) 3450.
Номер 1.
234 : 5 = 46 (ост. 4)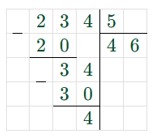
234 человека нельзя рассадить поровну в 5 автобусов, так как число 234 не делится на 5 нацело.
Ответ: нельзя.
Номер 2.
Вспомним, что число называется делителем другого числа, если при делении на него получается целый результат без остатка.Разложим число 60 на простые множители:
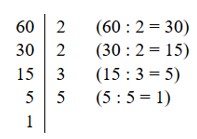
Делители числа 60:
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Номер 3.
Число делится на 9 если сумма цифр этого числа делится на 9.Двухзначное число состоит из десятков и единиц, по условию они равны.
Значит, двухзначное число, которое делится на 9 и состоит из одинаковых цифр – это число 99.
99 → 9 + 9 = 18 – делится на 9.
Ответ: число 99.
Номер 4.
Трёхзначное число состоит из сотен, десятков и единиц.По условию данное число нечётное и делится на 5, значит в разряде единиц стоит цифра 5.
Так как число не может начинаться с цифры 0, значит в сотнях стоит цифра 7, а в десятках – 0.
В итоге получается число 705.
Ответ: число 705.
Номер 5.
Вспомним, что число делится на 9, если сумма цифр этого числа делится на 9.Чтобы проверить могла ли Катя купить 9 одинаковых тетрадей за 357 рублей, нужно общую стоимость покупки разделить на количество тетрадей и если стоимость одной тетради будет целым числом, то могла.
Проверим делится ли число 357 на 9 нацело:
3 + 5 + 7 = 8 + 7 = 15 – не делится на 9.
Значит, Катя не могла купить 9 одинаковых тетрадей за 357 рублей.
Ответ: нет, не могла.
Номер 6.
Вспомним, что число делится на 3, если сумма цифр этого числа делится на 3.а) Рассмотрим сумму 321 + 459.
Проверим каждое слагаемое на делимость числа 3:
312 → 3 + 2 + 1 = 6 - делится на 3, значит число 312 делится на 3;
459 → 4 + 5 + 9 =18 - делится на 3, значит число 459 делится на 3.
Если каждое слагаемое делится на 3, то и сумма чисел тоже делится на 3.
Значит сумма 321 + 459 делится на 3.
Сделаем проверку:
(321 + 459) : 3 = 780 : 3 = 260.
Ответ: сумма 321 + 459 делится на 3.
б) Рассмотрим сумму 323 + 4571.
1) Проверим каждое слагаемое на делимость числа 3:
323 → 3 + 2 + 3 = 8 - не делится на 3, значит и число 323 не делится на 3;
4571 → 4 + 5 + 7 + 1 = 17 - не делится на 3, значит и число 4571 не делится на 3.
2) Проверим делится сумма чисел на 3, узнав сумму цифр двух слагаемых:
8 + 17 = 25 – не делится на 3, значит и сумма 323 + 4571 не делится на 3.
Сделаем проверку:
(323 + 4571) : 3 = 4894 : 3 = 1631 (ост. 1)
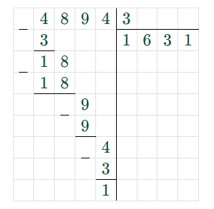
Ответ: сумма 323 + 4571 не делится на 3.
Номер 7.
а) Вспомним, если число оканчивается цифрой 0 или 5, то оно делится 5.Значит в число 345* вместо звёздочки можно подставить числа 0 или 5.
Получаются числа: 3450 и 3455.
б) Вспомним, что число делится на 9, если сумма цифр этого числа делится на 9. Любое число, которое делится на 9, делится и на 3.
Узнаем сумму цифр числа 345*:
345* → 3 + 4 + 5 + * = 12 + *
Ближайшее число, которое делится на 9 – это число 18, значит, чтобы число делилось на 9 нужно подставить цифру 6, тогда получится число 3456.
в) Если число делится на 10, то оно будет делиться и на 2 и на 5.
Чтобы число 345* делилось на 10, оно должно оканчиваться на 0.
Получиться число 3450.
Проверим делится ли число на 3.
3450 → 3 + 4 + 5 + 0 = 12 – делится на 3.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.