Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 106-107 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Проверьте себя
Проверочная работа "Упрощение выражений"
Проверочная работа № 1.
Запишите выражение и упростите его:
1. Сумма шести «икс» и двенадцати «икс».
2. Разность двадцати трёх «игрек» и «игрек».
3. Произведение четырёх «зэт» и пяти.
4. Произведение семи и суммы трёх «икс» и пяти.
Запишите уравнение и решите его:
5. Разность десяти «икс» и двух «икс» равна шестнадцати.
6. Сумма четырёх «игрек» и трёх «игрек» равна семи.
Верно ли высказывание (ответьте да или нет)?
7. Выражение (3а + 9) · 2 равно сумме трёх «а» и девяти.
8. Корень уравнения 5х – х = 20 — число четыре.
1. 6х + 12х = (6 + 12) · х = 18х
2. 23у – у = (23 – 1) · у = 22у
3. 4z · 5 = 20z
4. 7 · (3x + 5) = 7 · 3x + 7 · 5 = 21х + 35
5. 10х - 2х = 16
8х = 16
х = 16 : 8
х = 2
6. 4у + 3у = 7
7у = 7
у = 7 : 7
у = 1
7. (3а + 9) · 2 = 3а · 2 + 9 · 2 = 6а + 18 ≠ 3а + 9
Нет.
8. 5х – х = 20
4х = 20
х = 20 : 4
х = 5 ≠ 4
Нет.
Проверочная работа № 2.
Запишите выражение и упростите его:
1. Сумма двенадцати «игрек», шести «игрек» и «игрек».
2. К разности двадцати одного «эм» и девяти прибавить семь «эм».
3. Из суммы восьми «икс» и трёх «икс» вычесть одиннадцать.
Запишите уравнение и решите его:
4. Девять «икс» больше шести «икс» на шесть.
5. Пять «эм» меньше семи «эм» на восемь.
6. Четыре «бэ» впятеро меньше ста.
Верно ли высказывание (ответьте да или нет)?
7. Выражение 2а + 8 + 3а + 7 равно сумме пятнадцати и пяти «а».
8. Корень уравнения 4у · 15 = 120 — число два.
1. 12у + 6у + у = (12 + 6 + 1) · у = 19у
2. 21m - 9 + 7m = (21 + 7) · m – 9 = 28m – 9
3. 8х + 3х – 11 = (8 + 3) · х – 11 = 11х – 11
4. 9х – 6х = 6
3х = 6
х = 6 : 3
х = 2
5. 7m – 5m = 8
2m = 8
m = 8 : 2
m = 4
6. 4b · 5 = 100
20b = 100
b = 100 : 20
b = 5
7. 2а + 8 + 3а + 7 = (2а + 3а) + (8 + 7) = 5а + 15
Да.
8. 4у · 15 = 120
60у = 120
у = 120 : 60
у = 2
Да.
Проверочная работа № 3.
Запишите выражение и упростите его:
1. Разность четырёхсот трёх «игрек» и «игрек».
2. Сумма тридцати четырёх «эм» и шести, увеличенная на девять «эм».
Запишите уравнение и решите его:
3. Произведение трёх и разности двух «дэ» и пяти равно трём.
4. Восемь «икс» минус одиннадцать больше семи «икс» на единицу.
Запишите уравнение для решения задачи:
5. В справочнике помещены статьи о двух тысячах восьмистах сорока писателях и поэтах. Статей о поэтах помещено в нём «эм», а статей о писателях — вчетверо больше. Сколько в справочнике статей о поэтах?
6. Для приготовления фруктового напитка на восемь частей воды берут три части сиропа. Сколько сиропа потребуется для приготовления двадцати двух литров напитка? (Обозначьте объём одной части напитка х л.)
Верно ли высказывание (ответьте да или нет)?
7. Если упростить выражение k + 9 + 7k + 12 – 2k, то получится сумма семнадцати «ка» и десяти.
8. Корень уравнения 9у – у + 4у = 120 — число десять.
1. 403у – у = (403 – 1) · у = 402у
2. 34m + 6 + 9m = (34m + 9m) + 6 = 43m + 6
3. 3 · (2d – 5) = 3
2d – 5 = 3 : 3
2d – 5 = 1
2d = 1 + 5
2d = 6
d = 6 : 2
d = 3
4. (8x – 11) – 7x = 1
8х – 7х = 1 + 11
х = 12
5. m + 4m = 2840
5m = 2840
m = 568
6. 8x + 3x = 22
11x = 22
x = 2
7. k + 9 + 7k + 12 – 2k = (k + 7k – 2k) + (9 + 12) = 6k + 21
Нет.
8. 9у – у + 4у = 120
12у = 120
у = 120 : 12
у = 10
Да.
Проверьте себя
Проверочная работа № 1.
1. В магазине было 12 упаковок тетрадей в линейку, по 50 штук в каждой. За день продали 9 упаковок тетрадей. Сколько тетрадей осталось продать?
Решая эту задачу, ученики составили числовые выражения:
а) 12 ∙ 50 – 9 ∙ 50
б) 50 ∙ (12 – 9)
в) 12 ∙ 50 – 9
г) (12 – 9) ∙ 50.
Какое выражение не является решением задачи?
2. Упростите выражение:
а) а + 2а;
б) 25х – 19х
в) 18b ∙ 2 ∙ 5;
г) 5 ∙ (3t – t);
д) (21s + 79) ∙ 3.
3. Вычислите значение выражения, выбирая удобный способ:
а) 23 ∙ 21 + 23 ∙ 79;
б) 8 ∙ (25 + 7);
в) 74 ∙ 238 – 38 ∙ 74;
г) 208 ∙ 1001;
д) 99 ∙ 134.
4. Решите уравнение:
а) 8х + 7х = 1515;
б) 8 ∙ (2х – 6) = 128.
1. Выражение в) 12 ∙ 50 – 9 не является решением задачи.
2. а) а + 2а = 3а;
б) 25х – 19х = 6х;
в) 18b ∙ 2 ∙ 5 = 18b ∙ 10 = 180b;
г) 5 ∙ (3t – t) = 5 ∙ 2t = 10t;
д) (21s + 79) ∙ 3 = 3 ∙ 21s + 3 ∙ 79 = 63s + 237.
3. а) 23 ∙ 21 + 23 ∙ 79 = 23 ∙ (21 + 79) = 23 ∙ 100 = 2300;
б) 8 ∙ (25 + 7) = 8 ∙ 25 + 8 ∙ 7 = 200 + 56 = 256;
в) 74 ∙ 238 – 38 ∙ 74 = 74 ∙ (238 – 38) = 74 ∙ 200 = 14 800;
г) 208 ∙ 1001 = 208 ∙ (1000 + 1) = 208 ∙ 1000 + 208 ∙ 1 = 208 000 + 208 = 208 208;
д) 99 ∙ 134 = (100 – 1) ∙ 134 = 100 ∙ 134 – 134 ∙ 1 = 13 400 – 134 = 13 266.
4. а) 8х + 7х = 1515
15х = 1515
х = 1515 : 15
х = 101
Ответ: 101.
б) 8 ∙ (2х – 6) = 128
2х – 6 = 128 : 8
2х – 6 = 16
2х = 16 + 6
2х = 22
х = 22 : 2
х = 11
Ответ: 11.
Номер 1.
Рассмотрим задачу.Составим краткую запись задачи.
Было – 12 уп. по 50 тетр.
Продали – 9 уп.
Осталось – ?
Способ решения 1.
1) Узнаем сколько всего тетрадей в линейку изначально было в магазине.
Для этого количество упаковок (12 уп.) умножим на количество тетрадей в одной упаковке (50 тетр.).
12 · 50 = (10 + 2) · 50 = 500 + 100 = 600 (тетр.) – было изначально.
2) Умножим количество проданных упаковок (9 уп.) на количество тетрадей в одной упаковке (50 тетр.) и узнаем сколько тетрадей продали.
9 · 50 = 450 (тетр.) – продали.
3) Из всех тетрадей вычтем те тетради, которые продали и узнаем сколько тетрадей осталось продать.
600 – 450 = 150 (тетр.) – осталось продать.
Данное решение можно оформить выражением:
12 · 50 – 9 · 50 = 150 (тетр.).
Ответ: осталось продать 150 тетрадей.
Способ решения 2.
1) Узнаем сколько пачек тетрадей осталось продать.
12 – 9 = 3 (п.) – тетрадей осталось продать.
2) Умножим количество непроданных пачек тетрадей (3 п.) на количество тетрадей в одной упаковке (50 тетр.) и узнаем:
3 · 50 = 150 (тетрд.) – осталось продать.
Данное решение можно оформить выражением:
(12 – 9) · 50 = 50 · (12 – 9) = 150 (тетр.)
Ответ: 150 тетрадей осталось продать.
Получается, чтобы найти, сколько тетрадей в линейку осталось продать, можно составить следующие выражение:
1) 12 · 50 - 9 · 50;
2) 50 · (12 - 9);
3) (12 - 9) · 50.
Значит, решением задачи являются выражения под буквами а), б) и г), а выражение под буквой в) не является решением данной задачи.
Ответ: выражение в) 12 ∙ 50 – 9 не является решением задачи.
Номер 2.
Для упрощения выражения будем использовать переместительное, сочетательное и распределительное свойство умножения.а) а + 2а = (1 + 2) · а = 3а;
б) 25х – 19х = (25 – 19) · х = 6х;
в) 18b ∙ 2 ∙ 5 = (18 · 2 · 5) · b = 180b;
г) 5 ∙ (3t – t) = 5 · (3 – 1) · t = 5 ∙ 2t = (5 · 2) · t = 10t;
д) (21s + 79) ∙ 3 = (3 ∙ 21) · s + 3 ∙ 79 = 63s + 237.
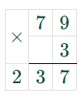
Номер 3.
При вычислении будем использовать распределительное свойство умножения.а) 23 ∙ 21 + 23 ∙ 79 = 23 ∙ (21 + 79) = 23 ∙ 100 = 2300.
Вынесем общий множитель 23 за скобку, в скобках останется сумма чисел 21 и 79. Вначале выполним сложение в скобках, а потом полученную сумму умножим на 23.
б) 8 ∙ (25 + 7) = 8 ∙ 25 + 8 ∙ 7 = 200 + 56 = 256.
Умножим общий множитель 8 на каждое слагаемое в скобках, получим 8 · 25 = 200 и 8 · 7 = 56, полученные произведения сложим.
в) 74 ∙ 238 – 38 ∙ 74 = 74 ∙ (238 – 38) = 74 ∙ 200 = 14 800.
Вынесем общий множитель 74 за скобку, в скобках останется разность чисел 228 и 38. Вначале выполним вычитание в скобках, а потом полученную разность умножим на 74.
г) 208 ∙ 1001 = 208 ∙ (1000 + 1) = 208 ∙ 1000 + 208 ∙ 1 = 208 000 + 208 = 208 208.
Разложим второй множитель на сумму чисел 1000 и 1, каждое слагаемое поочерёдно умножим на число 208, получим 208 · 1000 = 208 000 и 208 · 1 = 208. В итоге полученные результаты сложим.
д) 99 ∙ 134 = (100 – 1) ∙ 134 = 100 ∙ 134 – 134 ∙ 1 = 13 400 – 134 = 13 266.
Представим число 99 в виде разности (100 – 1). Уменьшаемое 100 и вычитаемое 1 поочерёдно умножим на 134, получим 100 · 134 = 13 400 и 134 · 1 = 134. Потом выполним вычитание и в результате получится 13 266.
Номер 4.
Вспомним, что чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.а) 8х + 7х = 1515;
Упростим левую часть уравнения применив распределительное свойство умножения:
(8 + 7) · х = 1515;
15х = 1515;
Найдём неизвестный множитель х:
х = 1515 : 15;
х = 101.
Ответ: х = 101.
Сделаем проверку:
8 · 101 + 7 · 101 = (8 + 7) · 101 = 15 · 101 = 15 · (100 + 1) = 15 · 100 + 15 · 1 = 1500 + 15 = 1515;
1515 = 1515 – верно.
б) 8 ∙ (2х – 6) = 128;
Найдём неизвестный множитель (2х – 6):
2х – 6 = 128 : 8;
2х – 6 = 16;
Теперь найдём неизвестное уменьшаемое 2х:
2х = 16 + 6;
2х = 22;
Найдём неизвестный множитель х:
х = 22 : 2;
х = 11.
Ответ: х = 11.
Сделаем проверку:
8 · (2 · 11 – 6) = 8 · (22 – 6) = 8 · 16 = 8 · (10 + 6) = 80 + 48 = 128;
128 = 128 – верно.
Проверочная работа № 2.
1. Запишите равенство и найдите, при каких значениях буквы оно будет верным:
а) сумма 3х и 8х равна 121;
б) разность 46у и 15у равна 186;
в) выражение 3а меньше 7а на 224;
г) выражение 9с больше 2с на 84;
д) 37b на 58 меньше, чем 280;
е) 6k втрое больше, чем 24.
2. Найдите значение выражения:
а) 13 ∙ 23 + 23 ∙ 10;
б) 200 ∙ 17 + 100 ∙ 17;
в) 154 ∙ 30 – 124 ∙ 30;
г) 687 ∙ 25 – 487 ∙ 25.
1.
а) 3х + 8х = 121
11х = 121
х = 121 : 11
х = 11
Ответ: 11.
б) 46у – 15у = 186
31у = 186
у = 186 : 31
у = 6
Ответ: 6.
в) 7а – 3а = 224
4а = 224
а = 224 : 4
а = 56
Ответ: 56.
г) 9с – 2с = 84
7с = 84
с = 84 : 7
с = 12
Ответ: 12.
д) 280 – 37b = 58
37b = 280 – 58
37b = 222
b = 222 : 37
b = 6
Ответ: 6.
е) 6k : 3 = 24
6k = 24 ∙ 3
6k = 72
k = 72 : 6
k = 12
Ответ: 12.
2. а) 13 ∙ 23 + 23 ∙ 10 = 23 ∙ (13 + 10) = 23 ∙ 23 = 529;
б) 200 ∙ 17 + 100 ∙ 17 = 17 ∙ (200 + 100) = 17 ∙ 300 = 5100;
в) 154 ∙ 30 – 124 ∙ 30 = 30 ∙ (154 – 124) = 30 ∙ 30 = 900;
г) 687 ∙ 25 – 487 ∙ 25 = 25 ∙ (687 – 487) = 25 ∙ 200 = 5000.
Номер 1.
Вспомним, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.а) Дано сумма 3х и 8х – это (3х + 8х) и по условию это равно 121.
Составим уравнение и решим его:
3х + 8х = 121;
Упростим левую часть уравнения применив распределительное свойство умножения:
(3 + 8) · х = 121;
11х = 121;
Найдём неизвестный множитель х:
х = 121 : 11;
х = 11.
Ответ: х = 11.
Сделаем проверку:
3 · 11 + 8 · 11 = 33 + 88 = 121;
121 = 121 – верно.
б) Дано разность 46у и 15у – это (46у – 15у) и по условию это равно 186.
Составим уравнение и решим его:
46у – 15у = 186;
Упростим левую часть уравнения применив распределительное свойство умножения:
(46 – 15) · у = 186;
31у = 186;
Найдём неизвестный множитель у:
у = 186 : 31;
у = 6.
Ответ: у = 6.
Сделаем проверку:
46 · 6 – 15 · 6 = (46 – 15) · 6 = 31 · 6 = 180 + 6 = 186;
186 = 186 – верно.
в) Вспомним, чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Известно, что выражение 3а меньше 7а на 224, значит уравнение будет выглядеть так:
7а – 3а = 224;
Упростим левую часть уравнения применив распределительное свойство умножения:
(7 – 3) · а = 224;
4а = 224;
Найдём неизвестный множитель а:
а = 224 : 4;
а = 56.
Ответ: а = 56.
Сделаем проверку:
7 · 56 – 3 · 56 = (7 – 3) · 56 = 4 · 56 = 4 · (50 + 6) = 200 + 24 = 224;
224 = 224 – верно.
г) Вспомним, чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Известно, что выражение 9с больше 2с на 84, значит уравнение будет выглядеть так:
9с – 2с = 84;
Упростим левую часть уравнения применив распределительное свойство умножения:
(9 – 2) · с = 84;
7с = 84;
Найдём неизвестный множитель с:
с = 84 : 7;
с = 12.
Ответ: с = 12.
Сделаем проверку:
9 · 12 – 2 · 12 = (9 – 2) · 12 = 7 · 12 = 7 · (10 + 2) = 70 + 14 = 84;
84 = 84.
д) Вспомним, чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Известно, что 37b на 58 меньше, чем 280, значит уравнение будет выглядеть так:
280 – 37b = 58;
Найдём неизвестное вычитаемое 37b (чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность):
37b = 280 – 58;
37b = 222;
Найдём неизвестный множитель b:
b = 222 : 37;
b = 6.
Ответ: b = 6.
Сделаем проверку:
280 – 37 · 6 = 280 - (30 + 7) · 6 = 280 – (180 + 42) = 280 – 180 – 42 = 100 – 42 = 58;
58 = 58 – верно.
е) Известно, что 6k втрое больше, чем 24, значит (6k : 3) равно 24.
Составим уравнение и решим его:
6k : 3 = 24;
Найдём неизвестное делимое 6k (чтобы найти неизвестное делимое, нужно частное умножить на делитель):
6k = 24 ∙ 3;
6k = 72;
Найдём неизвестный множитель k:
k = 72 : 6;
k = 12.
Ответ: k = 12.
Сделаем проверку:
6 · 12 : 24 = 72 : 24 = 3 (раза) – число 6k больше 24 в 3 раза.
Верно.
Номер 2.
При вычислении будем использовать распределительное свойство умножения.а) 13 ∙ 23 + 23 ∙ 10 = 23 ∙ (13 + 10) = 23 ∙ 23 = 23 · (20 + 3) = 460 + 69 = 529.
Вынесем общий множитель 23 за скобку, в скобках останется сумма чисел 13 и 10. Вначале выполним сложение в скобках, а потом полученную сумму умножим на 23.
б) 200 ∙ 17 + 100 ∙ 17 = 17 ∙ (200 + 100) = 17 ∙ 300 = 5100.
Вынесем общий множитель 17 за скобку, в скобках останется сумма чисел 200 и 100. Вначале выполним сложение в скобках, а потом полученную сумму умножим на 17.
в) 154 ∙ 30 – 124 ∙ 30 = 30 ∙ (154 – 124) = 30 ∙ 30 = 900.
Вынесем общий множитель 30 за скобку, в скобках останется разность чисел 154 и 124. Вначале выполним вычитание в скобках, а потом полученную разность умножим на 30.
г) 687 ∙ 25 – 487 ∙ 25 = 25 ∙ (687 – 487) = 25 ∙ 200 = 5000.
Вынесем общий множитель 25 за скобку, в скобках останется разность чисел 687 и 487. Вначале выполним вычитание в скобках, а потом полученную разность умножим на 25.
Проверочная работа № 3.
1. В саду стояла бочка для полива растений в бочке было х л воды. Составьте выражение для нахождения количества воды в бочке для каждого случая:
а) в бочку долили 5 л воды;
б) количество воды в бочке увеличили в 3 раза;
в) в бочку долили 3 л, а затем получившееся количество воды увеличили в 2 раза;
г) увеличили количество воды в бочке в 4 раза, а затем вылили из неё 8 л.
Найдите значение получившихся выражений, если в бочке было 30 л воды.
2. Чему равно значение выражения:
а) 32х + 12х + 10х + 54х при х = 11;
б) 432а – 321а – 100а – 10 при а = 7645;
в) 400 + 101n + 500 – 51n при n = 43?
3. Найдите корень уравнения:
а) 42х + 11х + 2х = 330;
б) 167х – 45х – 34х – 80х = 112.
1.
а) х + 5 при х = 30, то х + 5 = 30 + 5 = 35 (л)
б) 3х при х = 30, то 3х = 3 ∙ 30 = 90 (л)
в) (х + 3) ∙ 2 при х = 30, то (30 + 3) ∙ 2 = 33 ∙ 2 = 66 (л)
г) 4х – 8 при х = 30, то 4 ∙ 30 – 8 = 120 – 8 = 112 (л)
2. а) 32х + 12х + 10х + 54х = 108х
При х = 11, то 108х = 108 ∙ 11 = 1188.
б) 432а – 321а – 100а – 10 = 11а – 10
При а = 7645, то 11а – 10 = 11 ∙ 7645 – 10 = 84 095 – 10 = 84 085.
в) 400 + 101n + 500 – 51n = 900 + 50n
При n = 43, то 900 + 50n = 900 + 50 ∙ 43 = 900 + 2150 = 3050.
3. а) 42х + 11х + 2х = 330
55х = 330
х = 330 : 55
х = 6
Ответ: 6.
б) 167х – 45х – 34х – 80х = 112
8х = 112
х = 112 : 8
х = 14
Ответ: 14.
Номер 1.
а) В бочке было х литров воды, в неё долили 5 л воды и стало (х + 5) литров воды.б) В бочке было х литров воды, потом количество воды в бочке увеличили в 3 раза, значит стало 3х литров воды.
в) В бочке было х литров воды, в неё долили 3 л и стало (х + 3) литра воды.
Затем получившееся количество воды увеличили в 2 раза и получилось:
(х + 3) · 2 литров воды.
г) В бочке было х литров воды, увеличили количество воды в бочке в 4 раза и стало 4х литров воды.
Затем вылили из неё 8 литров и в итоге стало:
(4х – 8) литров воды.
Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число и выполнить вычисления.
Вместо неизвестного х подставим число 30.
а) х + 5;
Если х = 30, то х + 5 = 30 + 5 = 35 (л).
б) 3х;
Если х = 30, то 3х = 3 ∙ 30 = 90 (л).
в) (х + 3) ∙ 2;
Если х = 30, то (30 + 3) ∙ 2 = 33 ∙ 2 = 66 (л).
г) 4х – 8;
Если х = 30, то 4 ∙ 30 – 8 = 120 – 8 = 112 (л).
Номер 2.
Сначала упростим выражение, используя распределительное свойство умножения.А затем найдём значение буквенного выражения, подставив данное число вместо неизвестной переменной и выполним вычисления.
а) 32х + 12х + 10х + 54х = (32 + 12 + 10 + 54) · х = (44 + 64) · х = 108х.
Подставим в выражение вместо х число 11 и вычислим:
108х = 108 ∙ 11 = (100 + 8) · 11 = 1100 + 88 = 1188.
Ответ: выражение равно 1188 при х = 11.
б) 432а – 321а – 100а – 10 = (432 – 321 - 100) · а – 10 = 11а – 10.
Подставим в выражение вместо а число 7645 и вычислим:
11а – 10 = 11 ∙ 7645 – 10 = 84 095 – 10 = 84 085.
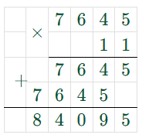
Ответ: выражение равно 84 085 при а = 7645.
в) 400 + 101n + 500 – 51n = (400 + 500) + (101 – 51) · n = 900 + 50n.
Подставим в выражение вместо n число 43 и вычислим:
900 + 50n = 900 + 50 ∙ 43 = 900 + 2150 = 3050.
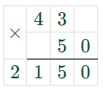
Ответ: выражение равно 3050 при n = 43.
Номер 3.
а) 42х + 11х + 2х = 330;Упростим левую часть уравнения применив распределительное свойство умножения:
(42 + 11 + 2) · х = 330;
55х = 330;
Найдём неизвестный множитель х:
х = 330 : 55;
х = 6.
Ответ: х = 6.
Сделаем проверку:
42 · 6 + 11 · 6 + 2 · 6 = 252 + 66 + 12 = 330;
330 = 330 – верно.
б) 167х – 45х – 34х – 80х = 112;
Упростим левую часть уравнения применив распределительное свойство умножения:
(167 – 45 – 34 – 80) · х = 112;
8х = 112;
Найдём неизвестный множитель х:
х = 112 : 8;
х = 14.
Ответ: х = 14.
Сделаем проверку:
167 · 14 – 45 · 14 – 34 · 14 – 80 · 14 = (167 – 45 – 34 – 80) · 14 = 8 · 14 = 8 · (10 + 4) = 80 + 32 = 112;
112 = 112 – верно.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.