Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – применяем математику на 77-78 странице

Шаг 1.
Найдём длину каждого маршрута от пункта Т в пункт В.

1) Рассмотрим маршрут ТАВ:
ТА + АВ = 226 км + 283 км = 509 км.

2) Рассмотрим маршрут ТАРВ:
ТА + АР + РВ = 226 км + 84 км + 352 км = 310 км + 352 км = 662 км.

3) Рассмотрим маршрут ТРАВ:
ТР + РА + АВ = 141 см + 84 см + 283 см = 225 см + 283 см = 508 (км).

4) Рассмотрим маршрут ТРВ:
ТР + РВ = 141 км + 352 км = 493км.

5) Рассмотрим маршрут ТРСВ:
ТР + РС + СВ = 141 км + 241 км + 294 км = 382 км + 294 км = 676 км.

6) Рассмотрим маршрут ТМСВ:
ТМ + МС + СВ = 94 км + 232 км + 294 км = 326 км + 294 км = 620 км.

7) Рассмотрим маршрут ТМСРВ:
ТМ + МС + СР + РВ = 94 км + 232 км + 241 км + 352 км = 326 км + 593 км = 919 км.

Шаг 2.
Расставим длины маршрутов в порядке возрастания:

493 км < 508 км < 509 км < 620 км < 662 км < 676 км < 919 км
Значит, самый короткий маршрут ТРВ = 493 км.

Ответ: самый короткий маршрут ТРВ = 493 км.

а) Нужно к дате начала Бородинской битвы (1818 г.) прибавить 200 лет и узнаем, когда праздновали 200 лет Бородинской битвы.
1812 + 200 = 2012 (год) – празднование 200 лет Бородинской битвы.

б) Ледовое побоище произошло на 570 лет раньше Бородинской битвы, значит от даты начала Бородинской битвы (1818 г.) нужно отнять 570 лет.
1812 - 570 = 1242 (год) – произошло Ледовое побоище.

в) Полтавская битва произошла на 467 лет позже Ледового побоища. Значит, к дате Ледового побоища (1242 г.) нужно прибавить 467 лет и получим:
1242 + 467 = 1709 (год) – произошла Полтавская битва.

г) Куликовская битва произошла на 329 лет раньше Полтавского сражения. Значит, из даты Полтавской битвы (1709 г.) нужно вычесть 329 лет.
1709 - 329 = 1380 (год) – произошла Куликовская битва.

д) Победа в Великой Отечественной войне произошла через 133 года после Отечественной войны с Наполеоном. К дате Бородинской битвы (1818 г.) нужно прибавить 133 года.
1812 + 133 = 1945 (год) – победа в Великой Отечественной войне.

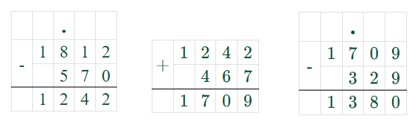
е) Начертим шкалу времени начиная с ХII века до XX в., где длина каждого века равна 3 клеткам.

1242 г – это почти середина 13 века;
1380 г – это конец 14 века;
1709 г – это начало 18 века;
1812 г – это начало 19 века;
1945 г – это почти середина 20 века.

Шаг 1.
Составим краткую запись к задаче:

Шаг 2.
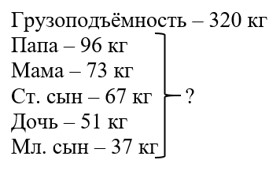
Найдём общий вес всех членов семьи, сложив вес каждого человека:

96 + 73 + 67 + 51 + 37 = 96 + 140 + 88 = 236 + 88 = 324 (кг) – вес всей семьи.

Шаг 3.
Сравним вес всей семьи с грузоподъёмностью лифта:

324 кг > 320 кг
Общий вес семьи больше грузоподъёмности лифта, значит семья в лифте поехать не сможет.

Ответ: семья не сможет поехать на лифте.

Шаг 1.
Составим краткую запись задачи:

Начало – 15 : 30
Дорога – 25 мин
Выйти – ? + 10 мин

Шаг 2.
Дорога занимает 25 минут, а прийти нужно за 10 минут до занятий.
Узнаем за сколько времени до занятий нужно выйти из дома, для этого сложим время:

25 + 10 = 35 (мин) – за сколько времени до начала занятия нужно выйти.

Шаг 3.
Полчетвёртого – это 15 ч 30 мин, а выйти из дома нужно за 35 минут, значит:

15 ч 30 мин – 35 мин = 14 ч + (60 мин + 30 мин – 35 мин) = 14 ч + (90 мин – 35 мин) = 14 ч 55 мин – время выхода из дома.

Ответ: из дома нужно выйти в 14 ч 55 мин.

Также задачу можно решить в виде выражения:
15 ч 30 мин – (25 мин + 10 мин) = 15 ч 30 мин – 25 мин – 10 мин = 15 ч 5 мин – 10 мин = 14 ч 55 мин.

Составим краткую запись к задаче:

Задание а.
1) Из школы вышли в 9 ч 15 мин.

2) На посадку потратили 15 минут, значит:
9 ч 15 мин + 15 мин = 9 ч 30 мин – начало поездки.

3) После начала поездки они приехали в музей через 1 ч 45 мин, значит:
9 ч 30 + 1 ч 45 мин = 10 ч + 75 мин = 10 ч + 1 ч 15 мин = 11 ч 15 мин – прибытие в музей.

4) Экскурсия закончилась через два с половиной часа – это 2 ч 30 мин:
11 ч 15 мин + 2 ч 30 мин = 13 ч 45 мин – окончание экскурсии.

5) Обратный путь составил на 30 минут дольше, чем путь до музея, значит:
1 ч 45 мин + 30 мин = 1 ч + 75 мин = 1 ч + 1 ч 15 мин = 2 ч 15 мин – обратный путь до школы;
Экскурсия закончилась в 13 ч 45 мин и обратно они ехали 2 ч 15 мин, значит:
13 ч 45 мин + 2 ч 15 мин = 15 ч + 60 мин = 15 ч + 1 ч = 16 ч 00 мин – прибытие обратно.

6) Через 10 минут они пришли в класс и начали обсуждать экскурсию:
16 ч 00 мин + 10 мин = 16 ч 10 мин – пришли в класс и начали обсуждать экскурсию.

7) 25 минут было обсуждение экскурсии, значит:
16 ч 10 мин + 25 мин = 16 ч 35 мин – закончили обсуждать экскурсию.

Этапы экскурсии:
1) Выход из школы – 9 : 15;
2) Начало поездки – 9 : 30;
3) Прибытие в музей – 11 : 15;
4) Окончание экскурсии – 13 : 45;
5) Приезд к школе – 16 : 00;
6) Пришли в класс и начали обсуждать экскурсию – 16 : 10;
7) Закончили обсуждение экскурсии – 16 : 35.

Задание б.
Узнаем сколько времени заняла экскурсия, для этого из времени конца экскурсии (16 ч 35 мин) нужно вычесть время выхода из школы (9 ч 15 мин).
16 ч 35 мин – 9 ч 15 мин = 7 ч 20 мин – время заняла экскурсия.

Ответ: 7 ч 20 мин заняла вся экскурсия.

Составим краткую запись к задаче:

Длина – 4 м
Ширина – 5 м
Дверь – 80 см
Р_пола – ?
Р_{потолка} – ?

1) Плинтус располагается по периметру потолка и пола.
Значит, чтобы узнать длину потолочного и напольного плинтуса, нужно найти периметр пола и потолка.
Потолок и пол имеют форму прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины.
(4 + 5) · 2 = 9 · 2 = 18 (м) – длина потолочного плинтуса.

2) Периметр пола и потолка одинаковый. Но при расчёте длины напольного плинтуса нужно вычесть длину двери.
Значит для напольного плинтуса понадобится на 80 см меньше. Вспомним, что 1 м = 100 см.
18 м – 80 см = (17 м + 1 м) – 80 см = 17 м + (100 см – 80 см) = 17 м 20 см – длина напольного плинтуса.

Ответ: 18 м – потолочного плинтуса и 17 м 20 см – напольного плинтуса.

Шаг 1.
Составим краткую запись к задаче:

Шаг 2.
Высота верхней секции шкафа на 35 см ниже нижней секции, также учитываем, что 1 дм = 10 см, то:

18 дм – 35 см = 180 дм – 35 дм = 145 дм = 14 дм 5 см – высота верхней секции шкафа.

Шаг 3.
Узнаем общую высоту шкафа сложив высоты каждой секции шкафа.

18 дм + 14 дм 5 см = 32 дм 5 см – высота шкафа из двух секций.

Шаг 4.
Сравним высоту шкафа с высотой потолка в комнате, учитывая, что 1 м = 100 см.

32 дм 5 см = 325 см = 3 м 25 см.
3 м 25 см > 2 м 70 см – высота потолка в комнате ниже высоты шкафа значит, шкаф нельзя разместить в этой комнате.

Ответ: шкаф нельзя разместить.

Шаг 1.
Составим краткую запись к задаче:

Шаг 2.
В магазине купили 1 кг 460 г помидоров, 2 кг 240 г огурцов, 1 кг 150 г перца и 300 г зеленого лука, узнаем общую массу всех овощей сложив все массы:

1 кг 460 г + 2 кг 240 г + 1 кг 150 г + 300 г = 3 кг 700 г + 1 кг 450 г = 5 кг 150 г – масса всех купленных продуктов.

Шаг 3.
Сравним массу всех купленных продуктов с грузоподъёмностью пакета.

5 кг 150 г > 5 кг – масса продуктов больше массы, которую выдерживает пакет, значит, покупатель не донесёт овощи до дома.

Ответ: покупатель не донесет овощи до дома.

Шаг 1.
Составим краткую запись к задаче:

Стоимость машины – 310 000 р. Заплатил – 81 200 р. Выплаты 3 года – по 7180 р. в месяц Переплата – ? р. 1) Максим должен выплатить кредит в течение трёх лет по 7180 рублей в месяц. Чтобы узнать сумму, которую он выплатит за 3 года нужно сумму, которую платит каждый месяц (7180 р.) умножить на 36 месяцев, так как 1 год = 12 мес., тогда 3 года = 12 мес. · 3 = 36 мес. 7180 · 36 = 258 480 (р.) – выплатит Максим за 3 года.

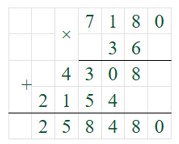
2) При покупке машины Максим заплатил 81 200 рублей и в течении трёх лет он ещё заплатит 258 480 рублей.
Сложим данные суммы и узнаем сколько всего он заплатит за машину.
258 480 + 81 200 = 339 680 (р.) – всего заплатит Максим за машину.

3) Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Значит из стоимости, которую Максим заплатил за машину (339 680 р.) нужно вычесть первоначальную стоимость машины (310 тыс. р. = 310 000 р.)
339 680 - 310 000 = 29 680 (р.) – переплатил Максим за машину.

Ответ: на 29 680 рублей больше Максим заплатит за машину.

Также задачу можно решить выражением:
(7180 · 12 · 3 + 81 200) – 310 000 = 29 680 (р.).

Задание а.

Рассмотрим вариант поездки на общественном транспорте.

1) Стоимость одного проезда на автобусе 50 рублей. У мамы и папы есть проездной билет на автобус, значит билет на автобус нужно купить только 4 детям.
50 · 4 = 200 (р.) - стоимость проезда всей семьи на автобусе.

2) Стоимость одного проезда на электричке 180 рублей. Нужно купить билеты для семьи из 6 человек. Умножим стоимость одного билета на количество человек и узнаем стоимость поездки на электричке.
180 · 6 = 1080 (р.) - стоимость проезда всей семьи на электричке.

3) Стоимость одного билета на маршрутном такси 40 рублей, значит стоимость поездки для 6 человек будет стоить:
40 · 6 = 240 (р.) - стоимость проезда всей семьи на маршрутном такси.

4) Сложим стоимость всех билетов и узнаем общую стоимость проезда на общественном транспорте для всей семьи.
200 + 1080 + 240 = 1280 + 240 = 1520 (р.) - общая стоимость проезда всей семьи на общественном транспорте.

Также вычисления стоимости поездки на общественном транспорте можно оформить в виде выражения:
50 · 4 + (180 + 40) · 6 = 200 + 220 · 6 = 200 + 1320 = 1520 (р.).

Поездка на такси вместимостью 6 человек будет стоить 1650 рублей.

Сравним поездку на общественном транспорте и на такси:
1520 р. < 1650 р.
Поездка на общественном транспорте выгоднее на 130 рублей.
1520 – 1650 = 130 (р.)

Задание б.

Наиболее рационально выбрать поездку на такси, так как разница в цене небольшая (130 р.), но будет комфортнее и быстрее доехать до заповедника.