Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – применяем математику на 156-157 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Сколько потребуется машин грузоподъёмностью 5 т для перевозки 428 рулонов линолеума шириной 15 дм и длиной 200 дм, если масса одного квадратного дециметра линолеума равна 25 г?
Ответ:1) 15 · 200 = 3000 (дм2) – площадь одного рулонного линолеума;
2) 428 · 3000 = 1 284 000 (дм2) – площадь 428 рулонов линолеума;

3) 1 284 000 · 25 = 32 100 000 (г) = 32 100 кг = 32 т 100 кг – масса всего линолеума;

4) 5 т = 5000 кг;
32 100 : 5000 = 6 (ост. 2100) – понадобится 7 машин.

Ответ: 7 машин.
Номер 2.
Новогодний подарок упакован в коробку в форме куба с ребром 45 см (рис. 119). Сколько требуется ленты для обвязки крест-накрест этой коробки, если на бантик нужно ещё 40 см?

1) 45 · 6 = 270 (см) – нужно ленты без бантика.
2) 270 + 40 = 310 (см) – всего нужно ленты.
Ответ: 310 см.
Номер 3.
Из листа бумаги размером 20 × 20 см вырезали прямоугольник со сторонами 12 × 18 см.
а) Можно ли из остатка вырезать квадрат со стороной 9 см?
б) Какой квадрат наибольшей площади можно вырезать из остатка и сколько?
а) 1) 20 – 12 = 8 (см) – осталось по ширине;
2) 20 – 18 = 2 (см) – осталось по длине;
Нет, нельзя так как 8 см < 9 см и 2 см < 9 см.
б) 2 · 2 = 4 (см2) – площадь наибольшего квадрата, который можно вырезать;
8 : 2 = 4 (шт.) – можно вырезать таких квадратов.
Ответ: а) нет; б) 4 см2, 4 квадрата.
Номер 4.
Вокруг прямоугольной клумбы проложили дорожку одинаковой ширины (рис. 120). Длина её внешнего края на 16 м длиннее внутреннего. Найдите ширину дорожки.

16 : 4 : 2 = 4 6 2 = 2 (м) – ширина дорожки.
Ответ: 2 м.
Номер 5.
На рисунке 121 изображён план квадратного участка, по углам которого растут четыре больших дерева. Владельцы участка хотят увеличить его площадь вдвое так, чтобы деревья остались вне участка и участок остался квадратным. Возможно ли это сделать?

Возможно, нужно развернуть участок, тогда его можно увеличить в 2 раза, не трогая деревья.

Номер 6.
Найдите массу детали, изготовленной из стального листа (рис. 122), если 1 cм2 этого листа имеет массу 45 г. Размеры на рисунке даны в сантиметрах.

Разделим деталь на 3 части.

1 часть: S = 10 · 3 = 30 cм2;
2 часть: S = 3 · 7 = 21 cм2;
3 часть: S = 7 · 3 = 21 cм2.
30 + 21 + 21 = 30 + 42 = 72 (cм2) – общая площадь детали.
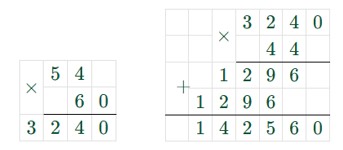
70 · 45 = 3240 (г) = 3 кг 240 г – масса детали.

Ответ: 3 кг 240 г.
Номер 7.
Вычислите объём своего класса. Сколько кубических метров воздуха приходится на одного ученика?
Ответ:Параметры класса: а = 8 м, b = 7 м, с = 3 м. В классе 23 ученика.
V = 8 · 7 · 3 = 168 м3.
168 : 23 = 7 (ост. 7) – примерно 7 м3 приходится на 1 ученика.

Номер 8.
Миша составил выражение для вычисления площади спортивной площадки на даче (см. план на рисунке 123):
(8 · 6) : 2 – 4 · 6 : 2.
Объясните его рассуждения и найдите значение этого выражения.

8 · 6 = 48 – площадь всего участка;
(8 · 6) : 2 = 48 : 2 = 24 – площадь половины участка;
4 · 6 : 2 = 24 : 2 = 12 - треугольная площадь слева, которая не занята площадкой;
(8 · 6) : 2 – 4 · 6 : 2 = 24 – 12 = 12 – площадь спортивной площадки.
Ответ: 12.
Номер 9.
На трёхъярусную клумбу нужно высадить цветы (рис. 124, а). На первый ярус высаживают тагетис (бархотцы), на второй – виолу (анютины глазки), а на третий – агератум. Норма высадки на 1 м2 тагетиса – 60 кустиков, виолы – 70 кустиков и агератума – 80 кустиков рассады. Рассчитайте, сколько кустиков каждой рассады надо заказать на клумбу, план которой представлен на рисунке 124, б. Размер стороны клетки 1 м.

1) 4 · 2 · 4 : 2 = 16 (м2) – площадь первого яруса;
2) 4 · 1 · 3 : 2 + 2 · 2 = 6 + 4 = 10 (м2) – площадь третьего яруса;
3) 6 · 6 – (16 + 10) = 36 – 26 = 10 (м2) – площадь третьего яруса;
4) 16 · 60 = 960 (кус.) – тагериса;
5) 10 · 70 = 700 (кус.) – виолы;
6) 10 · 80 = 800 (кус.) – агератума.
Ответ: 960 кустов; 700 кустов; 800 кустов.
Номер 10.
Рассчитайте, сколько коробок печенья надо заказать для изготовления 5300 новогодних подарков, если пачки печенья размером 10 × 6 × 4 см находятся в коробке размером 60 × 54 × 44 см.
Ответ:1) 10 · 6 · 4 = 10 · 24 = 240 (см3) – объем коробки печенья;
2) 60 · 54 · 44 = 2640 · 54 = 142 560 (см3) – объем коробки;

3) 142 560 : 240 = 594 (пачек) – печенья в коробке;

4) 5300 : 594 = 8 (ост. 548) – нужно заказать 9 коробок печенья.

Ответ: 9 коробок.
Номер 11.
Купили 100 плиток размером 15 × 30 см для ремонта пола в ванной комнате размером три с половиной метра на два.
а) Хватит ли этих плиток для ремонта?
б) Сколько целых плиток будет использовано при укладке пола?
в) Какое количество плиток надо докупить, чтобы настелить весь пол?
а)
1) 15 · 30 = 450 (см2) – площадь одной плитки;
2) 450 · 100 = 45 000 (см2) – площадь 100 плиток;
3) 3 м 50 см = 350 см и 2 м = 200 см;
350 · 200 = 70 000 (см2) – площадь пола;
4) 45 000 см2 < 70 000 см2 – плиток не хватит.
б) 70 000 : 450 = 7 000 : 45 = 155 (ост. 25) – нужно использовать 156 плиток.

в) 156 – 100 = 56 (пл.) – нужно докупить.
Ответ: а) нет; б) 156 плиток; в) 56 плиток.
Номер 12.
Бабушка попросила Лену, Олю, Таню и Ярослава прополоть две квадратные клумбы, у которых стороны равны 2 м и 4 м. Ярослав решил так: маленькая клумба в 2 раза меньше большой, поэтому я выполю сорняки на маленькой клумбе и оставлю девочкам прополку большой клумбы, чтобы им было меньше полоть. Будут ли согласны девочки с таким решением?
Ответ:1) 2 · 2 = 4 (м2) – площадь маленькой клумбы;
2) 4 · 4 = 16 (м2) – площадь большой клумбы;
3) 16 : 3 = 5 (ост. 1) – каждой девочке достанется более 5 м2;
4 м2 < 5 м2 – девочки выполют больше.
Ответ: девочки будут недовольны.
Номер 13.
Какими единицами объёма целесообразно измерять объём комнаты, пачки печенья, водохранилища?
Ответ:Объём комнаты в м3.
Объём пачки печенья в cм3.
Объём водохранилища в км3.
Номер 14.
Объём воды в озёрах земного шара около 230 000 км3.
а) Какой высоты будет башня в форме прямоугольного параллелепипеда, если его основание квадрат со стороной 0,5 м, а объём башни равен объёму воды в озёрах?
б) Сравните её длину с расстоянием от Земли до Луны. Недостающие данные найдите самостоятельно.
230 000 км3 = 230 000 000 000 000 м3 = 230 000 000 000 000 000 дм3 = 2300 · 1014 дм3 – объем воды.
а) 1) 50 · 50 = 2500 (см2) – 25 (дм2) – площадь основания.
2) 2300 · 1014 : 25 = 92 · 1014 (дм) = 92 · 1010 (км) – высота башни.
б) Среднее расстояние между центрами Земли и Луны – 384 467 км.
Высота башни больше расстояния от Земли до Луны.
Номер 1.
Сколько потребуется машин грузоподъёмностью 5 т для перевозки 428 рулонов линолеума шириной 15 дм и длиной 200 дм, если масса одного квадратного дециметра линолеума равна 25 г?
Ответ:1) 15 · 200 = 3000 (дм2) – площадь одного рулонного линолеума;
2) 428 · 3000 = 1 284 000 (дм2) – площадь 428 рулонов линолеума;

3) 1 284 000 · 25 = 32 100 000 (г) = 32 100 кг = 32 т 100 кг – масса всего линолеума;

4) 5 т = 5000 кг;
32 100 : 5000 = 6 (ост. 2100) – понадобится 7 машин.

Ответ: 7 машин.
Составим краткую запись задачи:
Машины – ? шт. по 5 т
Количество рулонов – 428 рулонов
Площадь рулона – 15 дм х 200 дм
Масса 1 дм2 рулона – 25 г
Рулон линолеума в развёрнутом виде имеет форму прямоугольника.
Площадь прямоугольника равна произведению его длины и ширины.
Найдём площадь одного рулона линолеума.
15 · 200 = 3000 (дм2) – площадь одного рулона линолеума.
Площадь одного рулона 3000 дм2, тогда узнаем площадь 428 рулонов линолеума.
3000 · 428 = 1 200 000 + 60 000 + 24 000 = 1 284 000 (дм2) – площадь всех рулонов линолеума.
Масса 1 дм2 линолеума равна 25 г.
Умножим массу 1 дм2 на площадь всех рулонов линолеума и узнаем общую массу линолеума.
Учитываем, что 1 кг = 1000 г.
25 · 1 284 000 = 32 100 000 (г) = (32 100 000 : 1000) = 32 100 (кг) – масса всех рулонов линолеума.
Вспомним, что 1 т = 1000 кг, тогда грузоподъемность одной машины 5 т = 5000 кг.
Разделим массу всех рулонов линолеума на грузоподъёмность одной машины и узнаем сколько таких машин понадобиться.
32 100 : 5000 = 6 (ост. 2100) ≈ 7 (машин).
Для перевозки линолеума потребуется 6 машин, которые будут заполнены полностью и одна машина – не полностью, значит потребуется 7 машин.
Ответ: для перевозки линолеума потребуется 7 машин.
Номер 2.
Новогодний подарок упакован в коробку в форме куба с ребром 45 см (рис. 4.34). Сколько требуется ленты для обвязки крест-накрест этой коробки, если на бантик нужно ещё 40 см?

1) 45 · 8 = 360 (см) – нужно ленты без бантика.
2) 360 + 40 = 400 (см) = 4 (м) – всего нужно ленты.
Ответ: 400 см = 4 м.
Составим кртакую запись задачи:

Чтобы обвязать коробку крест на крест, нужно 8 раз пройти через грань куба (так как верхнюю и нижнюю грань обвязывают 2 раза).
Умножим длину ребра куба (45 см) на 8 и узнаем сколько потребуется ленты без бантика.
45 · 8 = (40 + 5) · 8 = 320 + 40 = 360 (см) – потребуется ленты без бантика.
Также ещё нужно на бантик 40 см ленты, значит, всего для обвязки коробки потребуется:
360 + 40 = 400 (см) = 4 м – всего потребуется ленты.
Учитываем то, что 1 м = 100 см.
Ответ: 4 метра ленты потребуется.
Также задачу можно решить выражением:
45 · 8 + 40 = 360 + 40 = 400 (см) = 4 (м).
Номер 3.
Из листа бумаги размером 20 × 20 см вырезали прямоугольник со сторонами 12 × 18 см.
а) Можно ли из остатка вырезать квадрат со стороной 9 см?
б) Какой квадрат наибольшей площади можно вырезать из остатка?
а) 1) 20 – 12 = 8 (см) – осталось по ширине;
2) 20 – 18 = 2 (см) – осталось по длине;
Нет, нельзя так как 8 см < 9 см и 2 см < 9 см.

8 · 8 = 64 (см 2) – площадь наибольшего квадрата, который можно вырезать.
Ответ: а) нет; б) 64 см 2.
Лист бумаги – 20 х 20 см
Вырезали – 12 х 18 см
Можно вырезать – 9 х 9 см ?
а) Изначально лист бумаги имеет размер 20 х 20 см. По ширине вырезали 12 см, а по длине – 18 см.
Вычитанием узнаем сколько останется по ширине и по длине от листа бумаги.
1) 20 – 12 = 8 (см) – осталось по ширине;
2) 20 – 18 = 2 (см) – осталось по длине.
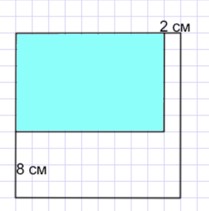
Квадрат со стороной 9 см нельзя вырезать, так как 8 см и 2 см меньше 9 см.
Ответ: нельзя вырезать.
б) Из остатка максимально можно вырезать квадрат со стороной 8 см.
Чтобы найти площадь квадрата нужно его сторону возвести в квадрат, значит его площадь будет равна:
82 = 8 · 8 = 64 (см2) – площадь максимального квадрата.
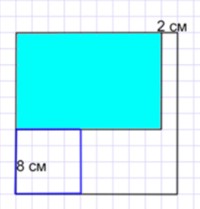
Ответ: из остатка можно вырезать квадрат с наибольшей площадью 64 см2.
Номер 4.
Вокруг прямоугольной клумбы проложили дорожку одинаковой ширины (рис. 4.35). Длина её внешнего края на 16 м длиннее внутреннего. Найдите ширину дорожки.

16 : 4 : 2 = 4 6 2 = 2 (м) – ширина дорожки.
Ответ: 2 м.
Пусть х метра – ширина дорожки. С каждой внутренней стороны длина будет меньше на х метра (таких 2 длины - справа и слева), тогда каждая сторона внутреннего прямоугольника меньше на 2х метра.
Таких дорожек 4, значит длина внутреннего края дорожки меньше на 4 · 2х = 8х метра и по условию это равно 16 м.
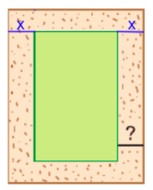
Составим уравнение и решим его:
8х = 16;
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
х = 16 : 8;
х = 2.
2 м – ширина дорожки.
Ответ: ширина дорожки равна 2 метра.
1) Узнаем во сколько раз длина её внешнего края больше длины внутреннего.
4 · 2 = 8 (раз).
2) Длина её внешнего края на 16 метров длиннее внутреннего и в 8 раз больше, значит:
16 : 8 = 2 (м) – ширина дорожки.
Ответ: 2 метра ширина дорожки.
Также задачу можно решить выражением:
16 : (4 · 2) = 16 : 8 = 2 (м).
Номер 5.
На рисунке 4.36 изображён план квадратного участка, по углам которого растут четыре больших дерева. Владельцы участка хотят увеличить его площадь вдвое так, чтобы деревья остались вне участка и участок остался квадратным. Возможно ли это сделать?

Возможно, нужно развернуть участок, тогда его можно увеличить в 2 раза, не трогая деревья.

Да, возможно.
Нужно развернуть участок, тогда его можно увеличить в 2 раза, не трогая деревья.
Площадь первоначального участка равна 4 треугольникам (см. рисунок), а площадь нового участка равна 8 таким же треугольникам, соответственно площадь будет увеличена в 2 раза.
В итоге получили участок квадратной формы и площадью в 2 раза больше.
8 : 4 = 2 (раза).
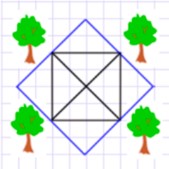
Номер 6.
Найдите массу детали, изготовленной из стального листа (рис. 4.37), если 1 cм2 этого листа имеет массу 45 г. Размеры на рисунке даны в сантиметрах.

Разделим деталь на 3 части.

1 часть: S = 10 · 3 = 30 cм2;
2 часть: S = 3 · 7 = 21 cм2;
3 часть: S = 7 · 3 = 21 cм2.
30 + 21 + 21 = 30 + 42 = 72 (cм2) – общая площадь детали.
72 · 45 = 3240 (г) = 3 кг 240 г – масса детали.

Ответ: 3 кг 240 г.
Разобьем деталь на 3 части: прямоугольник со сторонами 10 х 3 см и два прямоугольника со сторонами 7 х 3 см.
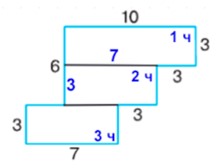
Составим краткую запись:
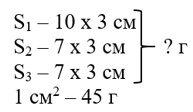
Найдём площадь каждой части. Площадь прямоугольника равна произведению его длины и ширины.
1) Стороны верхнего прямоугольника 10 см и 3 см, тогда его площадь равна:
10 · 3 = 30 (см2) – площадь первой части.
2) Стороны среднего и нижнего прямоугольников 7 см и 3 см, тогда их площадь равна:
7 · 3 = 21 (см2) – площадь второй и третьей части по отдельности.
3) Вспомним свойство площадей: площадь фигуры равна сумме площадей фигур, из которых она состоит.
Значит, сложим площади трёх частей и узнаем площадь всей детали.
30 + 21 + 21 = 72 (см2) – общая площадь детали.
4) По условию, 1 см2 стального листа имеет массу 45 г, а масса всей детали равна 72 см2.
При вычислении будем учитывать, что 1 кг = 1000 г.
72 · 45 = 3240 (г) = 3 кг 240 г – масса детали.
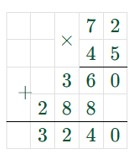
Ответ: 3 кг 240 г масса детали.
Номер 7.
Бабушка попросила Лену, Олю, Таню и Ярослава прополоть две квадратные клумбы, у которых стороны равны 2 м и 4 м. Ярослав решил так: маленькая клумба в 2 раза меньше большой, поэтому я выполю сорняки на маленькой клумбе и оставлю девочкам прополку большой клумбы, чтобы им было меньше полоть. Будут ли согласны девочки с таким решением?
Ответ:1) 2 · 2 = 4 (м2) – площадь маленькой клумбы.
2) 4 · 4 = 16 (м2) – площадь большой клумбы.
3) 16 : 3 = 5 (ост. 1) – каждой девочке достанется более 5 м2.
4 м2 < 5 м2 – девочки прополют больше.
Ответ: девочки будут недовольны.
Составим краткую запись задачи:
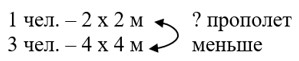
Вспомни, что площадь квадрата равна квадрату его стороны.
Ярослав выбрал прополоть маленькую квадратную клумбу со стороной 2 метра, узнаем её площадь.
22 = 2 · 2 = 4 (м2) – площадь маленькой клумбы.
Большая клумба имеет квадратную форму со стороной 4 метра, узнаем её площадь.
42 = 4 · 4 = 16 (м2) – площадь большой клумбы.
Три девочки должны прополоть клумбу с площадью 16 м2.
Узнаем какую площадь прополет каждая девочка.
16 : 3 = 5 (ост. 1) – каждой девочке достанется более 5 м2.
Сравним площади какую прополет Ярослав и каждая девочка.
4 м2 < 5 м2
Каждой девочки придётся выполоть больше, чем Ярославу. Значит, девочки не согласятся с Ярославом.
Ответ: девочки будут недовольны.
Номер 8.
Миша составил выражение для вычисления площади спортивной площадки на даче (см. план на рисунке 4.38):
(8 · 6) : 2 – 4 · 6 : 2.
Объясните его рассуждения и найдите значение этого выражения.

8 · 6 = 48 – площадь всего участка;
(8 · 6) : 2 = 48 : 2 = 24 – площадь половины участка;
4 · 6 : 2 = 24 : 2 = 12 – треугольная площадь слева, которая не занята площадкой;
(8 · 6) : 2 – 4 · 6 : 2 = 24 – 12 = 12 – площадь спортивной площадки.
Ответ: 12.
Разберём выражение, которое составил Миша, по действиям.
1) Миша умножил длину (4 + 4 = 8) и ширину участка, найдя при этом площадь всего участка.
8 · 6 – площадь всего участка.
2) Площадь всего участка Миша разделил на 2 и узнал площадь половины участка.
Так же это площадь состоит из маленького зелёного треугольника и бежевого треугольника (спортивной площадки).
(8 · 6) : 2 – площадь половины участка.
3) Теперь нужно найти площадь маленького зелёного треугольника слева. Для этого произведение длины и ширины треугольника разделили на 2.
4 · 6 : 2 – площадь маленького зелёного треугольника слева.
4) Теперь из площади половина участка Миша вычел площадь маленького зелёного треугольника слева и нашёл площадь спортивной площадки.
(8 · 6) : 2 – 4 · 6 : 2 – площадь спортивной площадки.
Выполним вычисления:
(8 · 6) : 2 – 4 · 6 : 2 = 48 : 2 – 24 : 2 = 24 – 12 = 12 – площадь спортивной площадки.
Ответ: площадь спортивной площадки равна 12.
Номер 9.
Рассчитайте, сколько коробок печенья надо заказать для изготовления 5300 новогодних подарков, если пачки печенья размером 10 × 6 × 4 см находятся в коробке размером 60 × 54 × 44 см, а в подарок кладут одну пачку печенья.
Ответ:1) 10 · 6 · 4 = 10 · 24 = 240 (см3) – объем коробки печенья.
2) 60 · 54 · 44 = 2640 · 54 = 142 560 (см3) – объем коробки.
3) 142 560 : 240 = 594 (пачек) – печенья в коробке.
4) 5300 : 594 = 8 (ост. 548) – нужно заказать 9 коробок печенья.

Ответ: 9 коробок.
Составим краткую запись задачи:
Всего – 5300 подарков
Подарок – 1 пачка печенья
Пачка печенья – 10 х 6 х 4 см
Коробка – 60 х 54 х 44 см
Кол-во коробок – ?
Вспомним, что объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Пачка печенья имеет форму прямоугольного параллелепипеда, которая имеет размеры 10 х 6 х 4 см.
Найдём объём одной такой пачки печенья.
10 · 6 · 4 = 10 · 24 = 240 (см3) – объём одной пачки печенья.
Коробка имеет форму прямоугольного параллелепипеда, которая имеет размеры 60 х 54 х 44 см, значит, объем одной такой коробки равен:
60 · 54 · 44 = 3240 · 44 = 142 560 (см3) – площадь одной коробки.
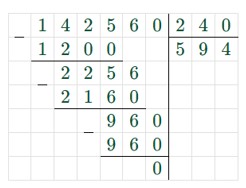
Найдем количество пачек печенья, которые умещает одна коробка, для этого разделим объём коробки на объём одной пачки печенья.
142 560 : 240 = 594 (пачек) – умещает одна коробка.
В одной коробке помещается 594 пачки печенья. А всего нужно изготовить 5300 новогодних подарков, в каждом из которых будет одна пачка печенья.
Значит разделим общее количество подарков на вместимость одной коробки и узнаем сколько коробок нужно заказать.
5300 : 594 = 8 (ост. 548) ≈ 9 (коробок).
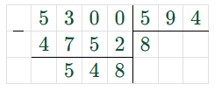
Нужно заказать 8 полных коробок с печеньем и одну коробку, которая будет заполнена не полностью, значит всего 9 коробок с печеньем.
Ответ: нужно заказать 9 коробок.
Номер 10.
Объём воды в озёрах земного шара около 230 000 км3.
а) Какой высоты будет башня в форме прямоугольного параллелепипеда, если его основание квадрат со стороной 0,5 м, а объём башни равен объёму воды в озёрах?
б) Сравните её длину с расстоянием от Земли до Луны. Недостающие данные найдите самостоятельно.
0, 5 м= 50 см – основание башни.
230 000 км3 = 230 000 000 000 000 м3 = 230 000 000 000 000 000 дм3 = 2300 · 1014 дм3 – объем воды.
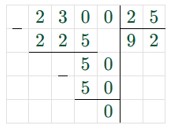
а) 1) 50 · 50 = 2500 (см2) – 25 (дм2) – площадь основания.
2) 2300 · 1014 : 25 = 92 · 1014 (дм) = 92 · 1010 (км) – высота башни.

б) Среднее расстояние между центрами Земли и Луны – 384 467 км.
Высота башни больше расстояния от Земли до Луны.

а) 1) 0,5 м – это половина метра, а 1 м = 10 дм, значит
1 м : 2 = 10 дм : 2 = 5 дм – длина и ширина основания башни.
2) Переведём объём воды в дм3.
Будем учитывать то, что число 10 в степени записывается так:
10 = 101, 100 = 102, 1000 = 103 и т.д.
1 км3 = 1 000 000 000 м3 = 109 м3, а 1 м3 = 1000 дм3 = 103 дм3.
230 000 км3 = (230 000 · 109 · 103) = 2300 · 1014 дм3 – объем воды.
3) Найдём площадь основания башни квадратной формы. Чтобы найти площадь квадрата нужно её сторону возвести в квадрат.
5 · 5 = 25 (дм2) – площадь основания башни.
4) Объём прямоугольного параллелепипеда равен произведению трёх его измерений – длины, ширины и высоты.
Чтобы найти высоту башни можно его объём разделить на произведение длины и ширины, то есть площадь основания.
А объём башни равен объёму воды в озёрах 2300 · 1014 дм3.
2300 · 1014 : 25 = (2300 : 25) · 1014 = 92 · 1014 (дм) = 92 · 1010 (км) – высота башни.
Ответ: высота башни равна 92 · 1010 км.
б) Сравним высоту башни с расстоянием от Земли до Луны.
Высота башни: 92 · 1010 км = 920 000 000 000 км
Расстояние от Земли до луны: 384 467 км
920 000 000 000 км > 384 467 км.
Высота башни больше, чем расстояние от Земли до Луны.
Ответ: высота башни больше.
Номер 11.
Прочитайте внимательно текст и выполните задания 1 – 6.
В начале июня Маша, Андрей и Лена приехали отдыхать к бабушке и дедушке в деревню Дальняя. Их участок (рис. 4.39) находится на пересечении улицы Солнечной и переулка Нужного. Калитка расположена со стороны переулка. Въезд машин в гараж находится со стороны улицы. При входе на участок слева от калитки находится дом, перед которым вдоль улицы растут вишни. Справа от калитки расположена хозяйственная постройка, в которой находится баня. Кроме дома, гаража и бани, есть маленький сарай для сельскохозяйственных инструментов рядом с яблоневым садом, огород, в котором располагаются теплица площадью 27 м2 и парник. Между домом и баней есть площадка, площадь которой равна 81 м2. Она замощена плиткой размером 50 х 50 см. Остальная площадь участка занята газоном, и на нём размещён батут, обозначенный цифрой 8.
Маша, Андрей и Лена решили помочь дедушке соединить дорожками шириной 1 м все хозяйственные постройки, которые планируется замостить такой же плиткой, как на площадке (на плане дорожки показаны серым цветом). А ещё они задумали разбить на газоне большую трёхъярусную клумбу, отмеченную на плане цифрой 9. На первом ярусе ребята хотят посадить тагетес (бархатцы), на втором – виолу (анютины глазки), а на третьем – агератум. Норма высадки на 1 м2 тагетеса – 60 кустиков, виолы – 70 кустиков и агератума – 80 кустиков рассады.
1. Определите на плане положение улицы и переулка.
2. Определите, какими цифрами на плане обозначены объекты, и заполните таблицу.

3. Найдите площадь дома и гаража в квадратных метрах.
4. Найдите расстояние от запланированной дорожки до батута.
5. Сколько упаковок плитки нужно купить для дорожек, если в упаковке 5 штук?
6. Определите размер клумбы. Сколько кустиков каждой рассады надо заказать для клумбы, план которой представлен на рисунке 4.40?


Задание 2.

Задание 3.
1) 12 ∙ 12 – 3 ∙ 6 = 144 – 18 = 126 (м2) – площадь дома;
2) 6 ∙ 9 = 54 (м2) – площадь гаража.
Ответ:126 м2 площадь дома и 54 м2 площадь гаража.
Задание 4.
Вариант 1. С учётом самой дорожки:
3 • 2 = 6 (м) - расстояние от запланированной дорожки до батута.
Вариант 2. Без учёта дорожки (ширина дорожки 1 м):
3 • 2 – 1 = 6 – 1 = 5 (м) – расстояние от запланированной дорожки до батута.
Задание 5.
1) 12 + 3 + 15 + 15 + 9 = 54 (м) – общая длина дорожки;
2) 54 ∙ 4 = 216 – понадобится;
3) 216 : 5 = 43 (ост.1) (упаковки) – значит нужно купить 44 упаковки.
Ответ:44 упаковки.
Задание 6.
1) 3 ∙ 3 = 9 (м2) – площадь всей клумбы;
2) 3 м : 6 = 300 см : 6 = 50 (см) – одна клетка на плане клумбы;
3) (1 • 2 : 2) • 4 = 4 (м2) – площадь под тагетес;

10 клеток составляет площадь под арегатум.
5) 10 ∙ (50 см ∙ 50 см) = 10 ∙ 2500 см2 = 25 000 см2 = 2 м2 5000 см2 – площадь под арегатум;
6) 80 ∙ 2 + 80 : 2 = 160 + 40 = 200 (кустиков) – рассады арегатума нужно заказать;
7) 9 м2 – 4 м2 – 2 м2 5000 см2 = 5 м2 – 2 м2 5000 см2 = 2 м2 5000 см2 – площадь под виолы;
8) 70 ∙ 2 + 70 : 2 = 140 + 35 = 175 (кустиков) – рассады виолы нужно заказать.

Ответ:размеры клумбы 3 х 3 м, её площадь 9 м2. Для клумбы нужно заказать 240 кустиков тагетеса, 175 кустиков виолы, 200 кустиков агератума.
Определите на плане положение улицы и переулка.
По условию калитка расположена со стороны переулка, значит переулок на плане находится снизу от участка.
Въезд машин в гараж находится со стороны улицы, значит улица на плане расположена слева от участка.
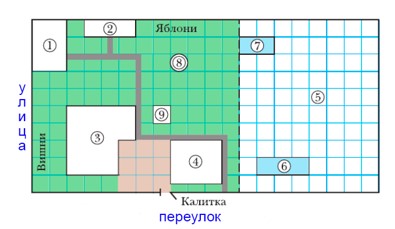
Ответ: улица – слева, переулок – снизу.
Определите, какими цифрами на плане обозначены объекты, и заполните таблицу.
1) При входе на участок слева от калитки находится дом, перед которым вдоль улицы растут вишни. Значит дом под цифрой 3.
2) Въезд машин в гараж находится со стороны улицы, значит гараж под номером 1.
3) Справа от калитки расположена хозяйственная постройка, в которой находится баня. Значит баня – номер 4.
4) Маленький сарай для сельскохозяйственных инструментов рядом с яблоневым садом. Сарай - номер 2.
5) Одна клетка на плане – 3 м, значит площадь одной клетки равна 3 · 3 = 9 м2. Теплица имеет площадь 27 м2, тогда теплица состоит из 3 клеток – и это номер 6.
27 : 9 = 3 (клетки) – теплица на плане.
6) Парник располагается в огороде (номер 5). Значит парник под номером 7.
Заполним таблицу:

Нагляднее показали на рисунке:
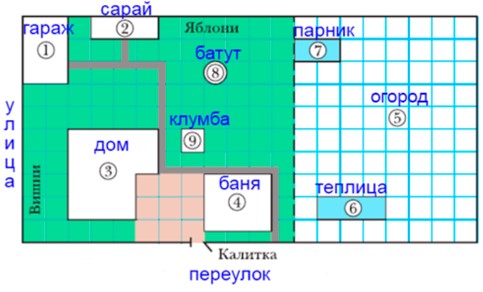
Найдите площадь дома и гаража в квадратных метрах.
Так как одна клетка равна 3 м, то площадь одной клетки равна 3 · 3 = 9 м2
1) Дом под номером 3 состоит из 14 клеток, а площадь одной клетки равна 9 м2, значит:
14 · 9 = (10 + 4) · 9 = 90 + 36 = 126 (м2) – площадь дома.
2) Гараж состоит из 6 клеток, значит:
6 · 9 = 54 (м2) – площадь гаража.
Ответ: площадь дома – 126 м2; площадь гаража – 54 м2.
Найдите расстояние от запланированной дорожки до батута.
Батут обозначен цифрой 8, а дорожка серым цветом.
На рисунке ниже показано какое расстояние нужно найти.
Расстояние от дорожки до батута 2 клетки, а длина одной клетки равна 3 м.
Рассмотрим 2 варианта.
1) С учётом самой дорожки:
3 · 2 = 6 (м) – расстояние от запланированной дорожки до батута с учётом самой дорожки.
2) Без учёта дорожки (ширина дорожки 1 м):
3 · 2 – 1 = 6 – 1 = 5 (м) – расстояние от запланированной дорожки до батута без учёта дорожки.
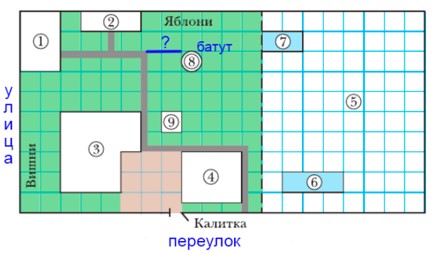
Сколько упаковок плитки нужно купить для дорожек, если в упаковке 5 штук?
1) Посчитаем сколько клеток занимает дорожка (серым цветом)
18 полных клеток по 3 метра и 1 неполная клетка по 1 метру – занимает дорожка.
2) Длина одной клетки 3 метра, значит длина всей дорожки:
18 · 3 + 1 = (10 + 8) · 3 + 1 = 30 + 24 + 1 = 55 (м) – длина дорожки.
Нагляднее показано на рисунке:
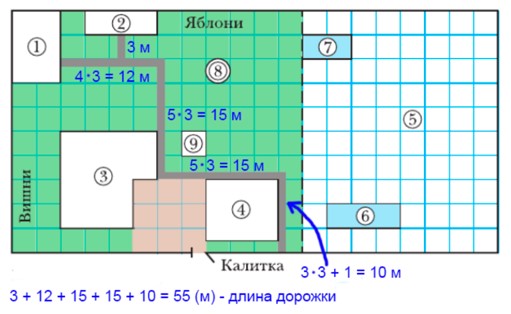
3) Ширина дорожки 1 метр. Узнаем площадь дорожки, умножив длину на её ширину.
55 · 1 = 55 (м2) – площадь дорожки.
4) Так как плитка имеет размеры 50 х 50 см, то на 1 м2 понадобится 4 такие плитки, так как:
1 м2 : (50 см · 50 см) = 10 000 см2 : 2500 см2 = 4 (плитки) – понадобится на 1 м2.
5) Так как на 1 м2 нужно 4 плитки, то на 55 м2 необходимо:
55 · 4 = (50 + 5) · 4 = 200 + 20 = 220 (плиток) – нужно всего.
6) В одной упаковке 5 плиток. Разделим общее количество плиток на вместимость одной упаковки и узнаем сколько нужно таких упаковок.
220 : 5 = 44 (упаковки) – нужно купить.
Ответ: нужно купить 44 упаковки плиток.
Определите размер клумбы. Сколько кустиков каждой рассады надо заказать для клумбы, план которой представлен на рисунке 4.40?
1) Трёхъярусную клумбу, отмеченная на плане цифрой 9 – это квадрат со стороной 3 метра. Узнаем её площадь.
3 · 3 = 9 (м2) – площадь клумбы.
2) Клумба имеет квадратную форму со стороной 3 метра. На плане клумба разделена на квадратики (6 по длине и 6 по ширине).
Узнаем длину и ширину одного такого квадратика.
3 м : 6 = 300 см : 6 = 50 см – длина и ширина одного квадратика.
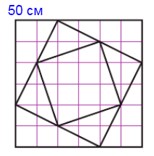
3) На первом ярусе ребята хотят посадить тагетес (бархатцы) – на плане закрашено жёлтым цветом.
Он состоит из 4 треугольников со сторонами 1 м и 2 м. Чтобы найти площадь треугольника нужно длину умножить на ширину и произведение разделить на 2.
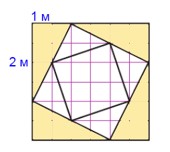
1 · 2 : 2 = 1 (м2) – площадь одного треугольника;
1 · 4 = 4 (м2) – площадь под тагетес.
4) На 1 м2 тагетеса – 60 кустиков рассады. А всего под тагетесы выделено 4 м2, значит
60 · 4 = 240 (к.) – рассады тагетеса нужно заказать.
5) На третьем ярусе хотят посадить агератум – на плане обозначено синим цветом.
Он состоит из квадрата со стороной 1 м и 4 треугольников со сторонами 150 см и 50 см.
Найдём площадь квадрата и 4 треугольников, а потом полученные площади сложим.
Чтобы найти площадь треугольника нужно длину умножить на ширину и произведение разделить на 2.
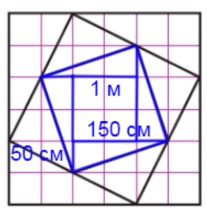
1 · 1 = 1 (м2) – площадь квадрата со стороной 1 м;
(150 · 50) : 2 = 7500 : 2 = 3750 (см2) – площадь одного треугольника;
3750 · 4 = 15 000 (см2) = 150 (дм2) – площадь 4 треугольников;
1 м2 + 150 дм2 = 100 дм2 + 150 дм2 = 250 дм2 = 25 000 см2 – площадь под арегатум.
6) Норма высадки на 1 м2 агератума – 80 кустиков рассады. Так как 1 м2 = 10 000 см2, то на 10 000 см2 арегатума нужно 80 кустиков рассады.
25 000 : 10 000 · 80 = (25 000 · 80) : 10 000 = 2 000 000 : 10 000 = 200 (к.) – рассады агератума нужно заказать.
7) На втором ярусе хотят посадить виолу (анютины глазки) – на плане фиолетовым цветом.
Чтобы найти его площадь из общей площади клумбы вычтем площадь тагетеса и арегатума. Учитываем, что 1 м2 = 10 000 см2.
9 м2 – 4 м2 – 25 000 см2 = 5 м2 – 25 000 см2 = 50 000 см2 – 25 000 см2 = 25 000 (см2) – площадь под виолу.
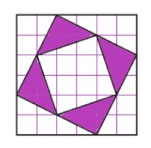
9) Площадь под виолу 25 000 см2. Норма высадки на 1 м2 = 10 000 см2 виолы – 70 кустиков, значит:
25 000 : 10 000 · 70 = (25 000 · 70) : 10 000 = 1 750 000 : 10 000 = 175 (к.) – рассады виолы нужно заказать.
Ответ: размеры клумбы 3 х 3 м, её площадь 9 м2.
Для клумбы нужно заказать 240 кустиков тагетеса, 175 кустиков виолы, 200 кустиков агератума.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.