Математика 5 класс учебник Виленкин, Жохов 1 часть ответы – номер 2.193

Математика 5 класс учебник Виленкин, Жохов, Чесноков

Тип: ГДЗ, Решебник.
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Александрова Л.А., Шварцбурд С.И.
Часть: 1.
Год: 2020-2024.
Издательство: Просвещение.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Номер 2.193.

Одна сторона треугольника равна 63 см, другая на 4 см больше, а третья на a см меньше второй стороны. Составьте выражение для нахождения периметра треугольника и найдите его значение при a = 8; a = 17.

Ответ:

Математика 5 класс учебник Виленкин, Жохов 1 часть, задание 3.133

63 + (63 + 4) + (63 + 4 – а) = 63 + 67 + 67 – а = 197 – а.
При а = 8, то 197 – а = 197 – 8 = 189 (см).
При а = 17, то 197 – а = 197 – 17 = 180 (см).

Ответ: 189 см; 180 см.

Шаг 1.
Составим краткую запись задачи:

Шаг 2.
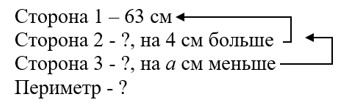
По условию вторая сторона треугольника на 4 см больше первой значит, чтобы найти длину второй стороны нужно к длине первой стороны прибавить 4 см.

63 + 4 = 67 (см) – длина второй стороны треугольника.

Шаг 3.
Третья сторона на а см меньше второй, значит, длину третьей стороны можно найти вычитанием.

67 – а (см) – длина третьей стороны треугольника.

Шаг 4.
Чтобы найти периметр треугольника нужно найти сумму длин его сторон.

63 + 67 + (67 - а) = (63 + 67 + 67) - а = 197 - а (см) – периметр треугольника.

Шаг 5.
Теперь найдём значение периметра, поставив в буквенное выражение значение переменной а и выполним вычисления.

1) а = 8, то 197 – а = 197 – 8 = 189 (см) – периметр треугольника.
2) а = 17, то 197 – а = 197 – 17 = 180 (см) – периметр треугольника.

Значит, если:
а = 8, то периметр треугольника равен 189 см;
а = 17, то периметр треугольника равен 180 см.

Ответ: 189 см; 180 см.

Конец страницы