Математика 4 класс учебник Петерсон 1 часть ответы – страница 91

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 1.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
а) Вырежи из бумаги прямоугольник ABCD со сторонами 4 см и 5 см. Разрежь его по диагонали AC на два треугольника. Докажи, что полученные треугольники равны. б) Сравни площади треугольников ABC и ADC сначала между собой, а затем – с площадью прямоугольника ABCD. Сделай вывод. в) Найди у треугольников ABC и ADC прямые углы. Как ты думаешь, почему такие треугольники называют прямоугольными?
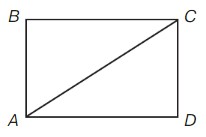
а)
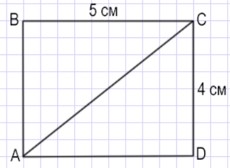
Получилось два треугольника ABC и ACD.
Треугольники ABС и АСD равны, так как у них все стороны равны:
AB = CD = 4 см; BC = AD = 5 см;
АС − общая.
При наложении треугольники совпадут.
б)
1) Рассмотрим треугольник АВС:
Полные клетки – 32;
Неполные клетки – 16.
32 + 16 : 2 ≈ 32 + 8 = 40 – площадь треугольника АВС.
Так как 1 см2 состоит из 4 клеток, то
40 : 4 ≈ 10 (см2) – площадь АВС.
2) Рассмотрим треугольник АСD:
Полные клетки – 32;
Неполные клетки – 16
32 + 16 : 2 ≈ 32 + 8 = 40 – площадь треугольника АD.
Так как 1 см2 состоит из 4 клеток, то
40 : 4 ≈ 10 (см2) – площадь АСD.
3) Рассмотрим прямоугольник АВСD:
5 · 4 = 20 (см2) – площадь прямоугольника АВСD.
4) Сравним площади.
Площади треугольников равны. SABC = SACD ≈ 10 см2.
SABCD = SABC + SACD = 10 + 10 = 20 см2
Вывод: Площадь прямоугольника равна площади двум его треугольникам.
в) Угол АВС – прямоугольный,
Угол АDC – прямоугольный.
Такие треугольники называют прямоугольными, так как один из углов у них равен 90°, то есть является прямым.
Номер 2.
Что общего у треугольников на рисунке? Назови катеты и гипотенузу каждого треугольника. Измерь их катеты и найди площадь.
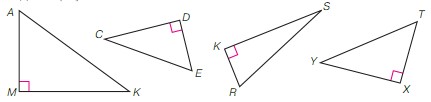
1) Треугольник AKM:
AМ и MK – катеты;
AК – гипотенуза.
Треугольник CDE:
CD и DE – катеты;
CE – гипотенуза.
Треугольник KSR:
KS и KR – катеты;
SR – гипотенузы.
Треугольник ТХУ:
ТХ и ХУ – катеты;
ТУ – гипотенуза.
2) Найдём площади:
AМ = 3 см; MK = 4 см;
3 · 4 : 2 = 12 : 2 = 6 (см2) – площадь треугольника АКМ.
CD = 3 см; DE = 2 см;
3 · 2 : 2 = 3 (см2) – площадь треугольника CDE.
KS = 40 мм и KR = 15 мм;
40 · 15 : 2 = 600 : 2 = 300 (мм2) = 3 (см2) – площадь треугольника KSR.
ТХ = 25 мм; ХУ = 32 мм;
25 · 32 : 2 = 800 : 2 = 400 (мм2) = 4 (см2) – площадь треугольника ТХУ.
Номер 3.
Начерти в тетради прямоугольный треугольник. Измерь его стороны и найди площадь.
Ответ: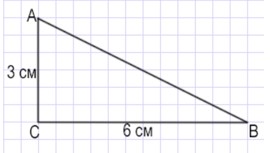
АС = 3 см
СВ = 6 см
3 · 6 : 2 = 18 : 2 = 9 (см2) – площадь треугольника АВС.
Ответ: 9 см2.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.