Математика 4 класс учебник Петерсон 1 часть ответы – страница 5

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 1.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Найди в тексте, выделенном рамкой вводную часть, главную мысль, примеры. Придумай свои примеры неравенств, множество решений которых являются: а) конечным; б) бесконечным; в) пустым. Сделай конспект.
Ответ:1) Вводная часть – это 1 абзац – выделим линией или знаком |. «У неравенства может быть несколько решений. Например, числа 1, 3, 5 являются решениями неравенства x < 6. Но это не все его решения: кроме них решениями являются числа 0, 2, 4. Если мы напишем числа 0, 1, 2, 3, 4, 5, то получим все решения неравенства x < 6. на множестве чисел N0 = {0, 1, 2, 3, ...}.»

2) Главная мысль – это 2 абзац – выделим двумя галочками или знаком ✓✓.
«Полный список решений неравенства называют множеством решений этого неравенства. (Мы будем искать решения только на изученном нами множестве чисел N0.)
3) Примеры – это 3, 4, 5 абзацы – выделим волнистой линией или символом ⸾.
«Так, множеством решений неравенства x < 6 является множество {0, 1, 2, 3, 4, 5}.
Неравенство y + 8 < 6 не имеет ни одного решения. Множество его решений является пустым: ∅.
Решениями неравенства z > 6 являются любые числа, большие 6. Данное неравенство имеет бесконечное множество решений: {7, 8, 9, 10, ...}.»

Примеры неравенств:
а) x < 5
N0 = {0, 1, 2, 3, 4};
б) x > 10
N0 = {11, 12, 13, ...}.
в) x + 5 < 5
Не имеет ни одного решения. Множество его решений является пустым: ∅.
Конспект:
1) Множество решений – это полный список решений неравенства.
2) У неравенства может быть несколько решений.
Пример: y < 6 {0, 1, 2, 3, 4, 5}.
Неравенство может быть пустым: ∅
Пример: y + 8 < 6 – не имеет ни одного решения.
Или бесконечно множество решений.
Пример: z > 6 {7, 8, 9 ...}.
Номер 2.
Запиши множество решений неравенства и отметь его на числовом луче. Существует ли в этом множестве наименьший элемент?
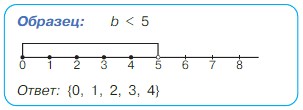
а) m > 4 б) m < 4 в) c > 3 г) c < 3
Ответ:а) m > 4
Ответ: {0, 1, 2, 3}
Наименьший элемент 0.
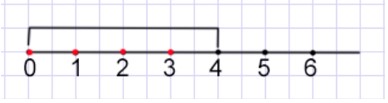
б) m < 4
Ответ: {5, 6, 7, ...}
Наименьший элемент 5.
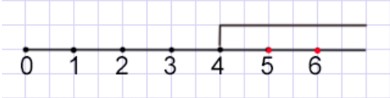
в) c > 3
Ответ: {4, 5, 6, ...}
Наименьший элемент 4.
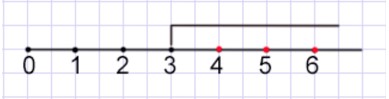
г) c < 3
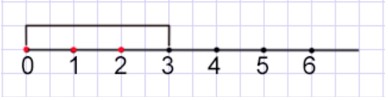
Ответ: {0, 1, 2} Наименьший элемент 0.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.