Математика 4 класс учебник Петерсон 1 часть ответы – страница 37

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 1.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 4.
Какие из чисел 7, 25, 124, 0 являются решениями данных неравенств:
а) x > 65 в) 4 · b ≥ 100 д) 7 ≤ t < 25 б) 6 + y < 12 г) 15 – a ≤ 45 е) 25 ≤ k ≤ 120
Ответ:а) x > 65
х = {66, 67, 68, ...}
Число 124 является решением данного неравенства;
б) 6 + y < 12
y < 12 – 6
y < 6
у = {0, 1, 2, 3, 4, 5}
Число 0 является решением данного неравенства;
в) 4 · b > 100
b > 100 : 4
b > 25
b = {26, 27, 28, ...}
Число 124 является решением данного неравенства;
г) 15 – a ≤ 45
a = {0, 1, 2, 3, ... , 14, 15}
Число 7 является решением данного неравенства;
д) 7 ≤ t < 25
t = {7, 8, 9, ..., 23, 24}
Число 7 является решением данного неравенства;
е) 25 ≤ k ≤ 120
k = {25, 26, 27, ..., 119, 120}
Число 25 является решением данного неравенства.
Номер 5.
На решение трёх задач Петя потратил a минут. Первую задачу он решал b минут, а вторую – на c минут дольше, чем первую. Сколько времени он решал третью задачу? Составь выражение и найди его значение при a = 25, b = 7, c = 5.
Ответ:a – (b + (b + c)) – решал Петя третью задачу, где b + c – решал Петя вторую задачу. При a = 25, b = 7, c = 5, то a – (b + b + c) = 25 – (7 + 7 + 5) = 25 – 19 = 6 (мин) – Петя решал третью задачу. Ответ: 6 минут.
Номер 6.
Прочитай число: 18 560 025. Что означает каждая из цифр 5 в записи этого числа? Какая цифра записана в разряде десятков тысяч? Сколько всего десятков тысяч в этом числе? Увеличь его на 9 единиц, в 9 раз. Уменьши на 9 единиц, в 9 раз.
Ответ:18 560 025 – восемнадцать миллионов пятьсот шестьдесят тысяч двадцать пять.
18 560 025 – цифра 5 означает сотни тысяч;
18 560 025 – цифра 5 означает единицы.
Цифра 6 записана разряде десятков тысяч.
В этом числе всего 6 десятков тысяч.
18 560 025 + 9 = 18 560 034
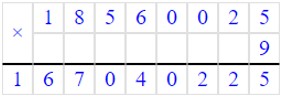
18 560 025 · 9 = 167 040 225
18 560 025 – 9 = 18 560 016
18 560 025 : 9 = 2 062 225.
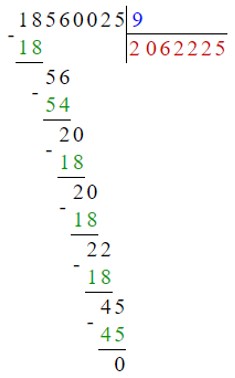
Номер 7.
Реши задачи. Что в них общего и различного?
а) Толя прочитал за 5 часов две книги. В первой книге было 126 страниц, а во второй – 84 страницы. Сколько времени он читал каждую книгу, если скорость его чтения не изменялась? б) Мотоциклист проехал до озера 126 км, а затем еще 84 км с той же скоростью. На весь путь он затратил 5 часов. Сколько времени мотоциклист ехал до озера и сколько потом?
- Придумай задачи с другими величинами, которые решаются так же.
а)

Решение:
1) 126 + 84 = 210 (стр.) – в двух книгах;
2) 210 : 5 = 42 (стр.) – скорость чтения за час;
3) 126 : 42 = 3 (ч) – читал первую книгу;
4) 84 : 42 = 2 (ч) – читал вторую книгу.
Ответ: 3 ч и 2 ч.
б)

1) 126 + 84 = 210 (км) – общее расстояние, которое мотоциклист проехал;
2) 210 : 5 = 42 (км/ч) – скорость мотоциклиста;
3) 126 : 42 = 3 (ч) – ехал до озера;
4) 84 : 42 = 2 (ч) – ехал после озера.
Ответ: 3 ч и 2 ч.
Общее в задачах: числа и решение задачи.
Различное: величины и тест задачи.
Задача:
Машинистка напечатала 126 страниц, а её помощница – 84 страницы.
Вместе они затратили на это 5 часов. Сколько часов они по отдельности печатали страницы, если их скорость печатания одинаковая?
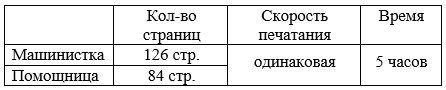
Решение: 1) 126 + 84 = 210 (стр.) – всего напечатали страниц; 2) 210 : 5 = 42 (стр.) – скорость печатания за 1 час; 3) 126 : 42 = 3 (ч) – печатала машинистка; 4) 84 : 42 = 2 (ч) – печатала помощница. Ответ: 3 часа и 2 часа.
Номер 8.
Имеются по одной гире в 1 кг, 2 кг, 4 кг, 8 кг, 16 кг. Докажи, что ими можно уравновесить любой груз массой m кг, где m < 32 и m ∈ N.
Ответ:Данными гирями можно уравновесить груз от 1 кг и до 31 кг, так как сумма этих гирь равна 31: 1 + 2 + 4 + 8 + 16 = 3 + 12 + 16 = 15 + 16 = 31.
Номер 9.
Вспомни и назови свойства действий с 0 и 1. Используя их, вычисли:
а) (418 : 418 – 0 · 75) · (62 – 62) + (89 · 1) : 89 б) (54 : 1 + 0 : 1) · 0 + (25 – 24) · (12 + 0 : 36)
Ответ:Свойства 0 и 1:
a · 0 = 0 – если число умножить на 0, то произведение равно 0;
a · 1 = a – если число умножить на 1, то произведение равно самому числу;
a + 0 = a – если к числу прибавить 0, то сумма равна самому числу;
a – a = 0 – если из числа вычесть само число, то разность равна 0;
a – 0 = a – если из числа вычесть 0, то получится само число;
0 : a = 0 – если 0 разделить на число, то частное равно 0;
a : a = 1 – если число разделить на само себя, то частное равно 1.
а) (418 : 418 – 0 · 75) · (62 – 62) + (89 · 1) : 89 = (1 – 0) · 0 + 89 : 89 = 1 · 0 + 1 = 0 + 1 = 1;
б) (54 : 1 + 0 : 1) · 0 + (25 – 24) · (12 + 0 : 36) = (54 + 0) · 0 + 1 · (12 + 0) = 54 · 0 + 1 · 12 = 0 + 12 = 12.
Номер 10.
Перенеси в тетрадь и заполни таблицу. Как можно упростить вычисления?


205 · 21 = 4305
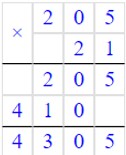
Чтобы упростить вычисления можно к последнему полученному результату нужно прибавлять 205.
205 · 23 = 4510 + 205 = 4715;
205 · 24 = 4715 + 205 = 4920;
205 · 25 = 4920 + 205 = 5125;
205 · 26 = 5125 + 205 = 5330.
Номер 11.
Продолжи ряд на три числа, сохраняя закономерность:
а) 101, 1002, 10003, ... б) 4, 9, 6, 18, 8, 27, ...
Ответ:а) Закономерность – к первому числу прибавляют 901, к следующему 9001, потом 90 001 и так далее.
101 + 901 = 1002;
1002 + 9001 = 10 003;
10 003 + 90 001 = 100 004;
100 004 + 900 001 = 1 000 005;
1 000 005 + 9 000 001 = 10 000 006.
Ответ: 101, 1002, 10 003, 100 004, 1 000 005, 10 000 006.
б) Закономерность: число, которое стоит на нечётном месте увеличивают на 2 и получают следующее число, стоящее на нечётном месте; а число стоящее на чётном месте увеличивают на 9 и получают следующее число, стоящее на чётном месте.
4 + 2 = 6 – третье число;
9 + 9 = 18 – четвертое число;
6 + 2 = 8 – шестое число;
18 + 9 = 27 – седьмое число;
8 + 2 = 10 – восьмое число;
27 + 9 = 36 – девятое число;
10 + 2 = 12 – десятое число.
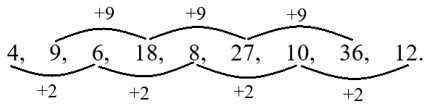
Ответ: 4, 9, 6, 18, 8, 27, 10, 36, 12.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.