Математика 3 класс учебник Петерсон 3 часть ответы – страница 66

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 3.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Продолжи ряд на два числа, сохраняя закономерность:
а) 0, 19, 38, 57 ... г) 1, 9, 25, 49, 81, 121 ...
б) 318, 422, 526 ... д) 0, 2, 6, 12, 20, 30 ...
в) 72574, 72561, 72548 ... е) 2, 3, 5, 8, 12, 17 ...
а) 0, 19, 38, 57, 76, 95, 114
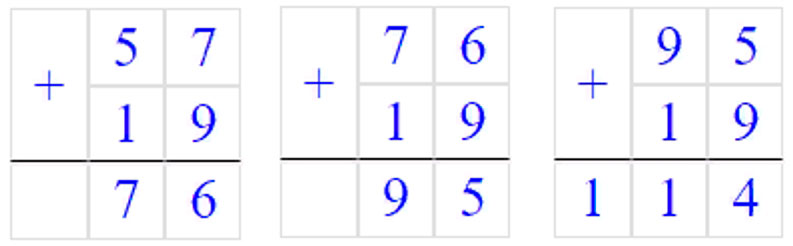
б) 318, 422, 526, 630, 734, 838
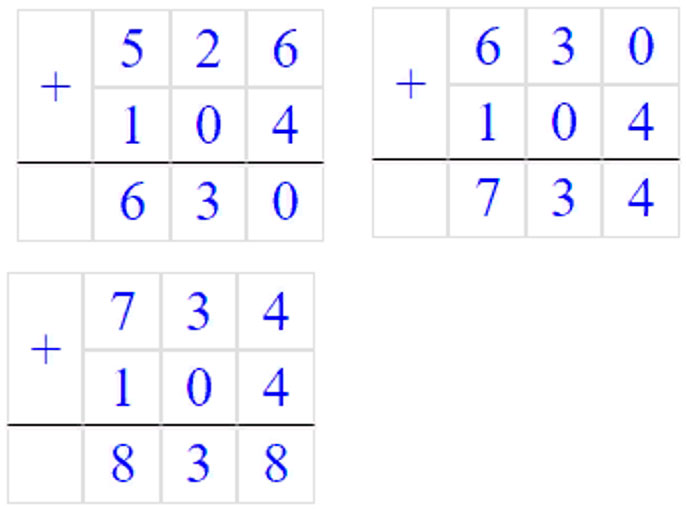
в) 72574, 72561, 72548, 72535, 72522, 72509
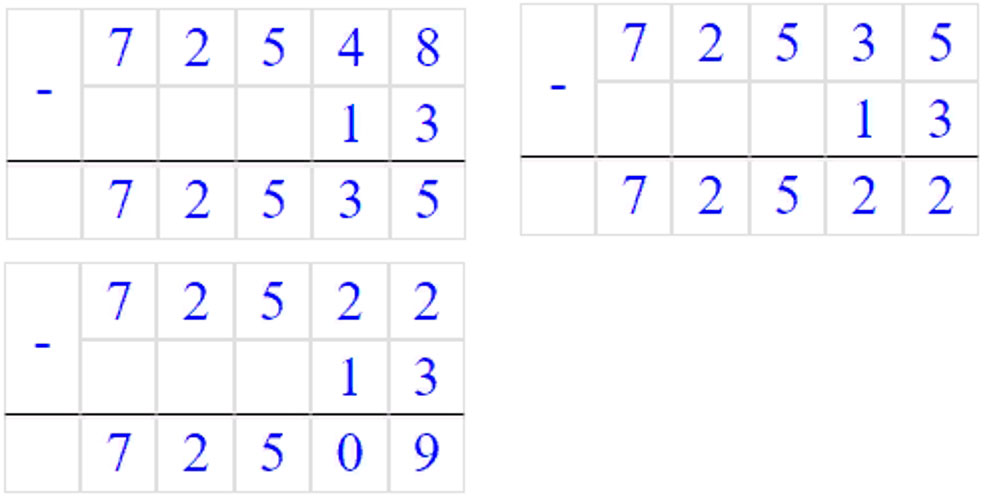
г) 1, 9, 25, 49, 81, 121, 169, 225, 289
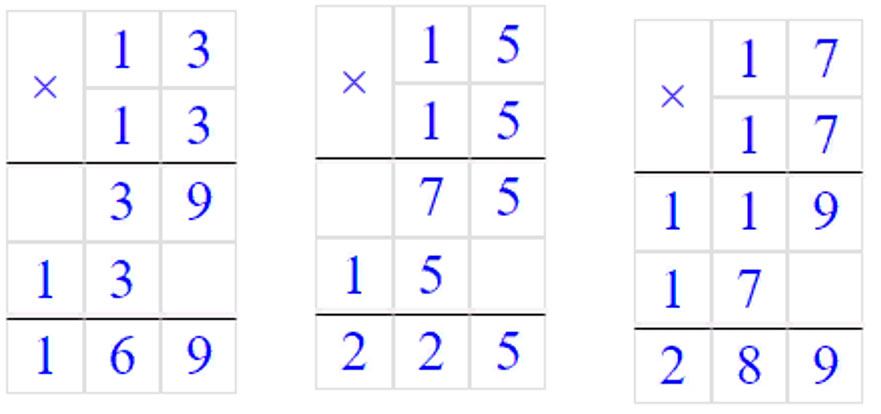
д) 0, 2, 6, 12, 20, 30, 42, 56, 72
е) 2, 3, 5, 8, 12, 17, 23, 30, 38
17 + 6 = 23, 23 + 7 = 30, 30 + 8 = 38
Номер 2.
Что общего в примерах каждого столбика? Объясни приёмы вычислений.
36 + 9 50 - 23 24 · 3
27 + 48 71 - 15 4 · 19
75 : 5 68 : 17
84 : 6 92 : 46
36 + 9 = 45
27 + 48 = 75
Сложить единицы, если двузначное число, то десятки сложить с десятками
50 - 23 = 27
71 - 15 = 56
Вычитаем единиц и десятки из десяток
24 · 3 = 72
4 · 19 = 76
Умножаем единицы на единицы и на десятки двузначного числа
75 : 5 = 15
(50 + 25) : 5 = 10 + 5 = 15
84 : 6 = 14
(60 + 24) : 6 = 10 + 4 = 14
Представим двузначное число в виде суммы разрядных или удобных слагаемых,
Разделим каждое слагаемое на это число,
Сложим полученные результаты.
68 : 17 = 4
28 : 7 = 4, поэтому по 4
92 : 46 = 2
12 : 6 = 2, поэтому по 2
Подбор по 2, по 3, по 4
Номер 3.
Запиши на математическом языке: а) переместительное свойство сложения и умножения; б) сочетательное свойство сложения и умножения; в) распределительное свойство умножения; г) правило деления суммы на число; д) правило вычитания числа из суммы; е) правило вычитания суммы из числа. Объясни их смысл.
Ответ:
а) a · b = b · a, a + b = b + a
От перестановки слагаемых местами их сумма не изменится.
От перестановки мест множителей произведение не меняется.
б) a + (b + c) = (a + b) + c, a · (b · c) = (a · b) · c
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Чтобы к сумме двух чисел прибавить третье число, можно к первому прибавить сумму второго и третьего чисел.
в) a · (b · c) = a · b + a · c
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
г) (a + b) : c = a : c + b : c
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и полученные результаты сложить.
д) a - (b + c) = a - b - c
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое.
е) a - (b + c) = a - b - c
Чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое.
Номер 4.
Пользуясь свойствами арифметических действий, упрости выражения:
99 + 1 + а 34 - (27 + с)
16 + b + 9 (d + 46) - 45
8 · m · 3 5 · х - 2 · х
n · 25 · 4 9 · у + у
99 + 1 + а = 100 + a
16 + b + 9 = 25 + b
34 - (27 + с) = 34 - 27 - c = 7 - c
(d + 46) - 45 = d + 46 - 45 = d + 1
8 · m · 3 = 24 · m
n · 25 · 4 = n · 100
5 · х - 2 · х = (5 - 2) · x = 3 · x
9 · у + у = (9 + 1) · y = 10 · y
Номер 5.
Вычисли наиболее удобным способом:
а) 32 + 34 + 36 + 38 г) (786 + 195) - 586
б) 5 · 19 · 5 · 3 · 2 · 2 д) 903 - 672 - 28
в) 47 · 15 + 53 · 15 е) 245 · 64 - 245 · 54
а) 32 + 34 + 36 + 38 = 70 + 70 = 140
б) 5 · 19 · 5 · 3 · 2 · 2 = 10 · 10 · 57 = 5700
в) 47 · 15 + 53 · 15 = (47 + 53) · 15 = 100 · 15 = 1500
г) (786 + 195) - 586 = 195 + (786 - 586) = 195 + 200 = 395
д) 903 - 672 - 28 = 903 - (672 + 28) = 903 - 700 = 203
е) 245 · 64 - 245 · 54 = 245 · (64 - 54) = 245 · 10 = 2450
Номер 6.
БЛИЦтурнир
а) У Ани а марок, а у Тани на с марок меньше. Сколько марок у Ани и Тани вместе?
б) Купили n слив. За обедом съели х слив, а за ужином – k слив. Сколько слив осталось?
в) Было d красных шариков и k синих. Их разделили поровну на 3 человек. Сколько шариков досталось каждому?
г) Артём поймал а рыбок, а Юра – в 4 раза больше. На сколько рыбок меньше поймал Артём, чем Юра?
д) После того как в саду посадили 4 ряда вишен по t вишен в ряду, осталось посадить ещё m вишен. Сколько всего вишен должны посадить в саду?
а) a + (a - с) (марок)
Ответ: a + (a - с) марок у Ани и Тани вместе.
б) n - х - k (слив)
Ответ: n - х - k слив осталось.
в) (d + k) : 3 (шариков)
Ответ: (d + k) : 3 шариков досталось каждому?
г) 4 · а - а = а · (4 - 1) = 3 · а (рыбок)
Ответ: на 3 · а рыбок меньше поймал Артём, чем Юра.
д) 4 · t + m (вишен)
Ответ: 4 · t + m всего вишен должны посадить в саду.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.