Математика 3 класс учебник Петерсон 3 часть ответы – страница 12

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 3.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 3.
Расстояние от деревни до станции 40 км. Всадник едет из деревни на станцию со скоростью 14 км/ч. Успеет ли он доскакать до станции за 3 часа?
Ответ:
14 · 3 = 42 (км)
Ответ: не успеет он доскакать до станции за 3 часа.
Номер 4.
Туристы решили пройти за день 30 км. Они уже прошли 3 ч со скоростью 6 км/ч. Какое расстояние им осталось пройти? За какое время они пройдут это расстояние, двигаясь с прежней скоростью?
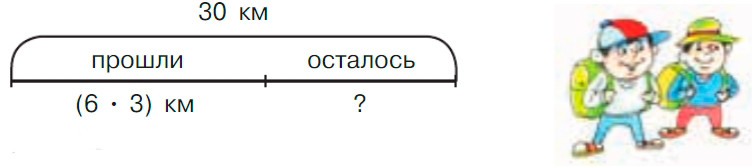
30 - 6 · 3 = 30 - 18 = 12 (км)
12 : 6 = 2 (ч)
Ответ: 12 километров им осталось пройти. За 2 часа они пройдут это расстояние, двигаясь с прежней скоростью.
Номер 5.
БЛИЦтурнир*
а) Маша прошла n км. Чему равна её скорость, если она затратила на путь k часов?
б) Лена шла a ч со скоростью b км/ч. Какое расстояние она прошла за это время?
в) Витя пробежал x метров за 5 мин, а Саша – за 6 мин. У кого из них скорость больше и на сколько?

а) n : k (км/ч)
Ответ: n : k км/ч её скорость, если она затратила на путь k часов.
б) a · b (км)
Ответ: a · b километров она прошла за это время.
в) Витя - x : 5 (м/мин), а Саша – х : 6 (м/мин), x : 6 - х : 5 = х : (6 - 5) = х : 1 = х (м/мин)
Ответ: у Саши из них скорость больше и на х м/мин.
Номер 6.
Какие свойства сложения и вычитания выражают данные равенства? Объясни их смысл, используя графические модели.
1) a - (b + c) = (a - b) - c = (a - c) - b
2) (a + b) - c = (a - c) + b = a + (b - c)

a - (b + c) = (a - b) - c = (a - c) - b − свойство вычитания числа из суммы: чтобы из числа вычесть сумму чисел, можно сначала вычесть одно из слагаемых, а затем второе.
(a + b) - c = (a - c) + b = a + (b - c) − свойство вычитания числа из суммы: чтобы из суммы вычесть число, можно из первого слагаемого вычесть число и прибавить второе слагаемое, или к первому слагаемому прибавить разность второго слагаемого и числа.
Номер 7.
Вычисли наиболее удобным способом:
а) 894 - (294 + 80) в) (586 + 245) - 486 д) 232 - (95 + 132)
б) 715 - 99 - 101 г) (324 + 498) - 298 е) (629 + 56) - 629
а) 894 - (294 + 80) = 894 - 294 + 80 = 680;
б) 715 - 99 - 101 = 715 - (99 + 101) = 515;
в) (586 + 245) - 486 = 586 - 486 + 245 = 345;
г) (324 + 498) - 298 = 324 + 498 - 298 = 524;
д) 232 - (95 + 132) = 232 - 132 - 95 = 5;
е) (629 + 56) - 629 = 629 - 629 + 56 = 56.
Номер 8.
Реши уравнения с комментированием и сделай проверку:
а) (a · 80) : 4 = 120
б) 9 · (560 : b - 5) = 27
в) (14 - c) · 4 - 9 = 19
а) (a · 80) : 4 = 120
а = (120 · 4) : 80
а = 6
Проверка: (6 · 80) : 4 = 120
б) 9 · (560 : b - 5) = 27
b = 560 : (27 : 9 + 5)
b = 560 : 8
b = 70
Проверка: 9 · (560 : 70 - 5) = 27
в) (14 - c) · 4 - 9 = 19
с = 14 - (19 + 9) : 4
с = 7
Проверка: (14 - 7) · 4 - 9 = 19
Номер 9.
Составь программу действий и вычисли:
а) (6543508 + 34592) : 9 - 700900 · 70 : 100
б) 81650204 - (54867 + 295 · 60) : 9 + 2989685
а) (6543508 + 34592) : 9 - 700900 · 70 : 100 = 240270
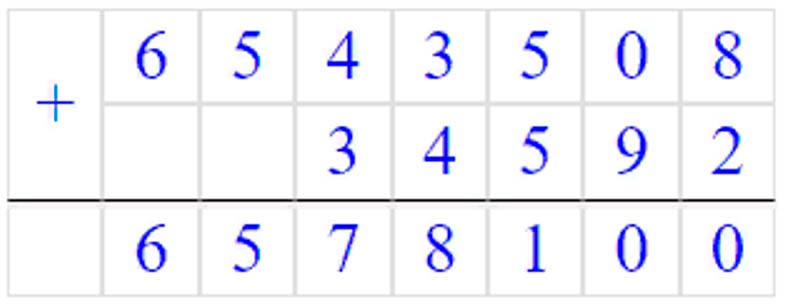
6543508 + 34592 = 6578100
6578100 : 9 = 730900
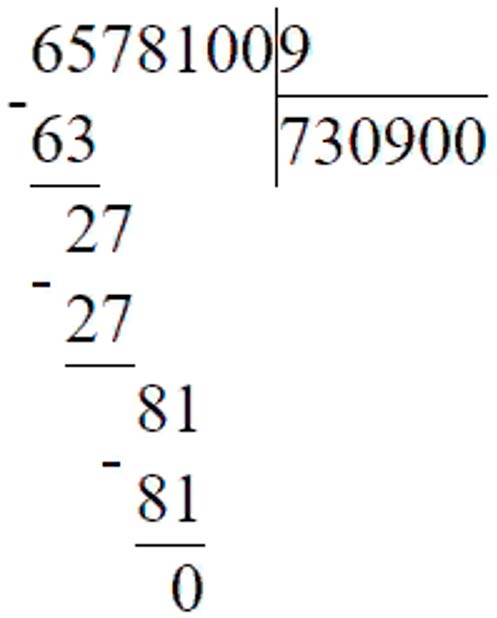
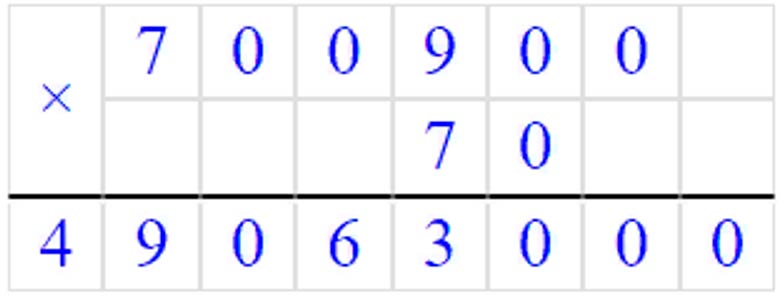
700900 · 70 = 49063000
49063000 : 100 = 490630
730900 - 490630 = 240270
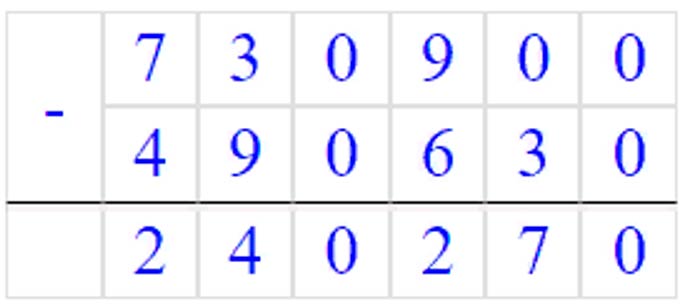
б) 81650204 - (54867 + 295 · 60) : 9 + 2989685 = 84631826
295 · 60 = 17700
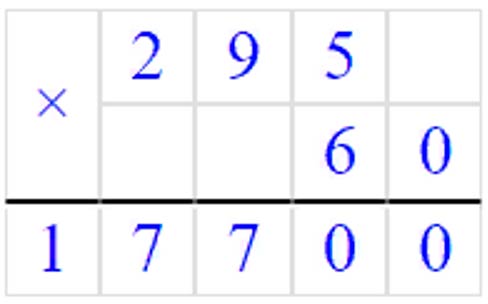
54867 + 17700 = 72567
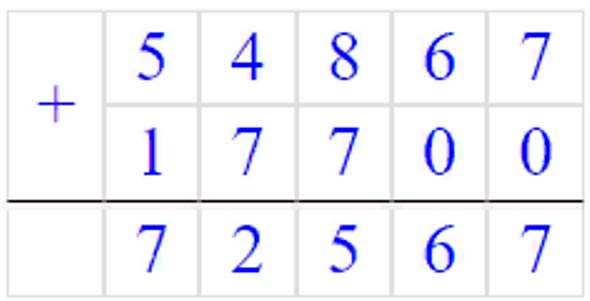
72567 : 9 = 8063
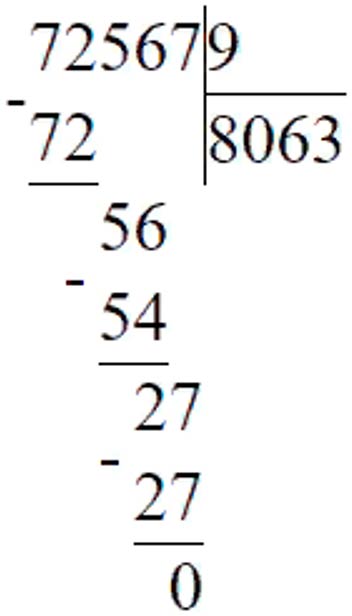
81650204 - 8063 = 81642141
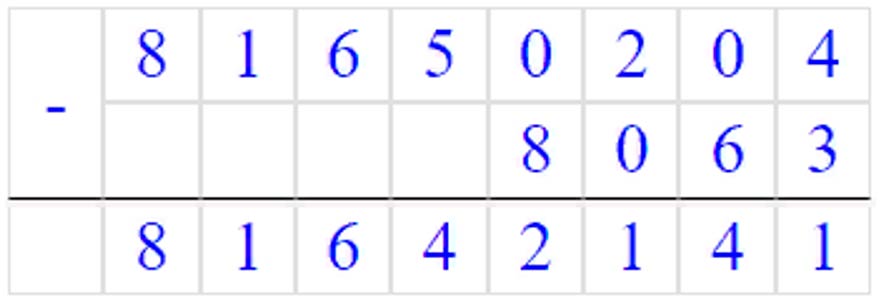
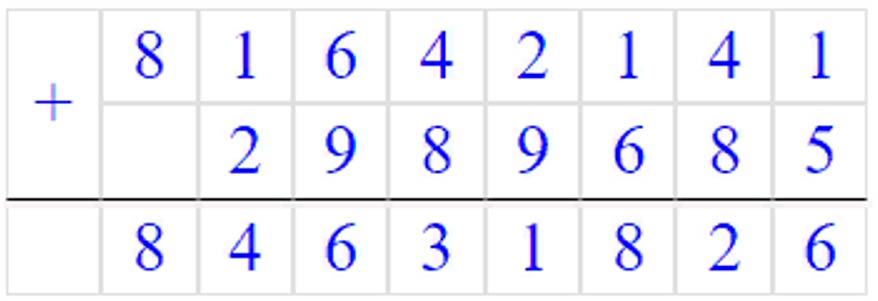
81642141 + 2989685 = 84631826
Номер 10.
1 января 2018 года было понедельником. Каким днём недели будет 1 января 2019 года, 1 января 2020 года, 1 января 2021 года?

1 января 2019 года – это вторник, 1 января 2020 года – среда, 1 января 2021 года – пятница. Дни идут по порядку, кроме 1 января 2021. 2020 является високосным годом - в нём 366 дней - добавляется 29 февраля).
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.