Математика 3 класс учебник Петерсон 2 часть ответы – страница 94

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 2.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Урок 41
Формула деления с остатком
Номер 4.
Запиши формулу деления с остатком. Пользуясь этой формулой, найди делимое а, если:
1) b = 7, c = 4, r = 1;
2) b = 12, c = 6, r = 3.
а = b ⋅ c + r, где
Делимое – а;
Делитель – b;
Частное – c;
Остаток – r < b.
1) a = 7 ⋅ 4 + 1 = 29;
2) a = 12 ⋅ 6 + 3 = 75.
Номер 5.
Выполни деление с остатком и сделай проверку:
А) 1662 на 7;
Б) 4764 на 5;
В) 3458 на 4;
Г) 36 529 на 6;
Д) 63 570 на 7;
Е) 46 476 на 8.

Номер 6.
А) Нужно перевезти 48 т зерна. Какое минимальное количество пятитонных грузовиков для этого потребуется?
Б) Мешок сахара стоит 600 р. Сколько таких мешков сахара можно купить на 5000 р.? Сколько денег еще останется?
А)

48 : 5 = 9 (ост. 3).
Будет 9 пятитонных полных грузовиков, но останутся еще 3 тонны зерна, которые нужно перевезти. Значит, всего грузовиков будет 10.
Ответ: 10 грузовиков.
Б)

5 000 : 600 = 8 (ост. 200).
Получается, что после покупки остаются 200 рублей, значит, можно купить только 8 мешков.
Ответ: можно купить 8 мешков и 200 рублей останутся.
Номер 8.
Запиши формулу деления с остатком для случая, когда остаток равен 0. Как можно назвать в этом случае числа a, b и с?
Ответ:а = b ⋅ c, где а – делимое, b – делитель, с – частное.
Номер 9.
Рассмотри решение примера:
600 : 70 = 60 д. : 7 д. = 8 (ост. 4 д.) = 8 (ост. 40).
Почему при делении с остатком круглых чисел в остатке надо приписать отброшенное число нулей? Вычисли и сделай проверку:
А) 160 : 30;
Б) 290 : 60;
В) 430 : 40;
Г) 920 : 50;
Д) 3800 : 900;
Е) 6700 : 200;
Ж) 21 400 : 70;
З) 576 200 : 800.
При делении с остатков круглых чисел в остатке надо приписать отброшенное число нулей, потому что в делимом и делителе их одинаковое количество отбрасывают, а затем нужно вернуть.
А) 160 : 30 = 16 дес. : 3 дес. = 5 (ост. 1 дес.) = 5 (ост. 10);
Проверка: 5 ⋅ 30 + 10 = 160;
Б) 290 : 60 = 29 дес. : 6 дес. = 4 (ост. 5 дес.) = 4 (ост. 50);
Проверка: 4 ⋅ 60 + 50 = 290;
В) 430 : 40 = 43 дес. : 4 дес. = 10 (отс. 3 дес.) = 10 (ост. 30);
Проверка: 10 ⋅ 40 + 30 = 430;
Г) 920 : 50 = 92 дес. : 5 дес. = 18 (ост. 2 дес.) = 18 (ост. 20);
Проверка: 18 ⋅ 50 + 20 = 920;
Д) 3800 : 900 = 38 сот. : 9 сот. = 4 (ост. 2 сот.) = 4 (ост. 200);
Проверка: 4 ⋅ 900 + 200 = 3800;
Е) 6700 : 200 = 67 сот. : 2 сот. = 33 (ост. 1 сот.) = 33 (ост. 100);
Проверка: 33 ⋅ 200 + 100 = 6700;
Ж) 21 400 : 70 = 2140 дес. : 7 дес. = 305 (ост. 5 дес.) = 305 (ост. 50);
Проверка: 305 ⋅ 70 + 50 = 21 400;
З) 576 200 : 800 = 5762 сот. : 8 сот. = 720 (ост. 2 сот.) = 720 (ост. 200);
Проверка: 720 ⋅ 800 + 200 = 576 200.
Номер 10.
Прочитай числа:
75 994 608;
75 994 600 315;
70 000 031;
712 021;
99 999.
Расположи эти числа в порядке возрастания.
99 999 – девяносто девять тысяч девятьсот девяносто девять;
712 021 – семьсот двенадцать тысяч двадцать один;
70 000 031 – семьдесят миллионов тридцать один;
75 994 608 – семьдесят пять миллионов девятьсот девяносто четыре тысячи шестьсот восемь;
75 994 600 315 – семьдесят пять миллиардов девятьсот девяносто четыре миллиона шестьсот тысяч триста пятнадцать.
Номер 11.
Реши уравнения с комментированием по компонентам действий:
14 – 81 : х = 5;
(у – 3) : 5 = 30;
(m ⋅ 4 + 6) : 9 = 2.

Номер 12.
Шапка стоит х р., а шарф – у р. Объясни смысл выражений:
х + у;
х – у;
х : у;
х ⋅ 5 + у ⋅ 2;
х ⋅ 3 + у ⋅ 3;
(х + у) ⋅ 3;
х ⋅ 8 – у ⋅ 8;
(х – у) ⋅ 8
x + у – общая стоимость шапки и шарфа;
x – у – на сколько шапка дороже шарфа;
x : у – во сколько раз шапка дороже шарфа;
x ⋅ 5 + у ⋅ 2 – сколько вместе стоят 5 шапок и 2 шарфа;
x ⋅ 3 + у ⋅ 3 – общая стоимость трех шапок и трёх шарфов;
(х + у) ⋅ 3 – общая стоимость трех комплектов из шапки и шарфа;
x ⋅ 8 – у ⋅ 8 – на сколько дороже 8 шапок, чем 8 шарфов;
(х – у) ⋅ 8 – на сколько дороже 8 шапок, чем 8 шарфов.
Номер 13.
Найди все способы размена 10 р. монетами в 1 р., 2 р. и 5 р. (количество монет не ограничено.)
Ответ:
10 рублей:
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1;
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 2;
1 + 1 + 1 + 1 + 1 + 5;
1 + 1 + 1 + 2 + 5;
1 + 1 + 1 + 2 + 1 + 1 + 2;
1 + 1 + 1 + 1 + 2 + 2 + 2;
1 + 1 + 2 + 2 + 2 + 2;
1 + 5 + 2 + 2;
5 + 5;
2 + 2 + 2 + 2 + 2.
Номер 14.
Половина половины числа равна 10. Какое это число?
Ответ: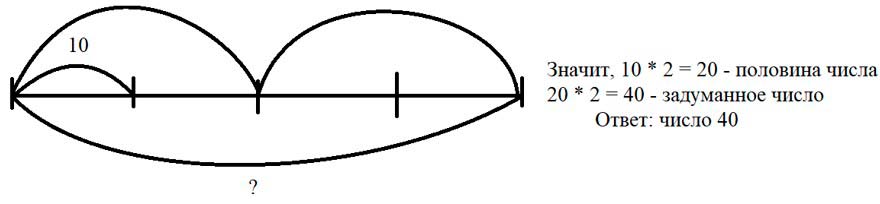
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.