Математика 3 класс учебник Петерсон 2 часть ответы – страница 64

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 2.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Урок 26
Решение задач
Номер 8.
Прочитай выражения а + b и а – b разными способами. Найди их значения, если:
1) а = 445 556, b = 99 999;
2) а = 172 094, b = 76 135.

Сумма чисел а и b; первое слагаемое а, второе слагаемое – b.
Разность чисел а и b; уменьшаемое а, вычитаемое b.
Номер 9.
Запиши число, которое:
А) на 5 больше числа р;
Б) на 5 меньше числа р;
В) в 5 раз больше числа р;
Г) в 5 раз меньше числа р.
А) р + 5;
Б) р – 5;
В) р ⋅ 5;
Г) р : 5.
Номер 10.
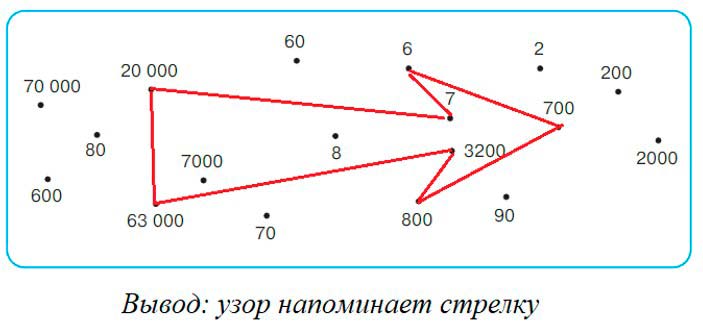
Вычисли. Наложи прозрачную пленку и соедини ответы по порядку. Что получилось?
1.20 ⋅ 40;
2.800 ⋅ 4;
3.70 ⋅ 900;
4.5000 ⋅ 4;
5.4900 : 700;
6.360 : 60;
7.5600 : 8;
8.24 000 : 30.
Номер 11.
Составь и реши уравнения:
А) на сколько надо разделить число 125 880, чтобы получить 6?
Б) какое число надо разделить на число 900, чтобы получить 5097?
В) какое число надо умножить на 50, чтобы получить 1 222 000?

Номер 12.
Арифметический ребус.
Мишу спросили: «Три да три да три – что будет?»
Он ответил: «Дыра». Это записали так:
ТРИ + ТРИ + ТРИ = ДЫРА.
(одинаковые буквы обозначают одинаковые цифры, а разные буквы – разные цифры). Известно, что:
(Ы + Ы) : Ы = Ы.
Какие цифры зашифрованы в этой записи?
Узнаю, чему равна Ы в выражении (ы + ы) : ы = ы.
Она равна 2, потому что (2 + 2) : 2 = 2.
Тогда, подставляем:
ТРИ + ТРИ + ТРИ = Д2РА.
Если оставить только первые буквы, то получится: Т + Т + Т = Д2, т.е. двузначное число с двойкой на конце.
Это может быть число 4, потому что 4 + 4 + 4 = 12.
Значит, Т = 4, Д = 1.
Тогда подставляю: 4РИ + 4РИ + 4РИ = 12РА.
Смотрим на букву Р и видим, что Р + Р + Р = Р, что возможно только при Р = 0, значит, Р = 0.
40И + 40И + 40И = 120А.
И и А – это точно не 1, 2, 4, 0.
Пусть это число 3. Тогда:
403 + 403 + 403 = 1209.
Ответ: Т = 4, Р = 0, И = 3, А = 9.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.