Математика 3 класс учебник Петерсон 2 часть ответы – страница 41
- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 2.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Урок 16
Симметрия относительно прямой
Номер 3.
Скопируй рисунки в тетради по клеточкам. Построй точки, симметричные данным относительно прямой l. Проверь правильной построений с помощью измерений и с помощью кальки.
Ответ: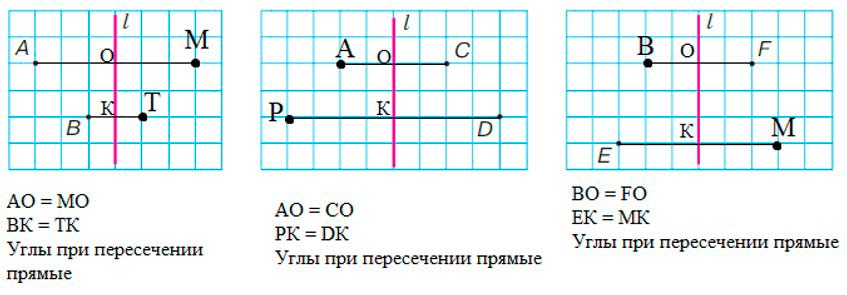
Номер 4.
Построй в тетради отрезки, симметричные данным относительно прямой l. Как можно проверить, правильно ли они построены?
Ответ: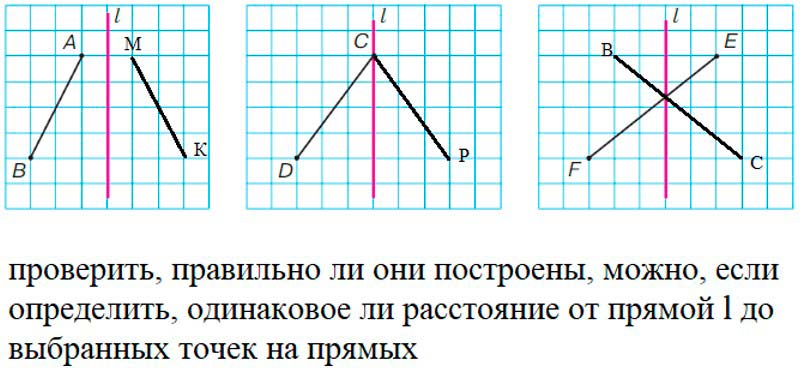
Номер 5.
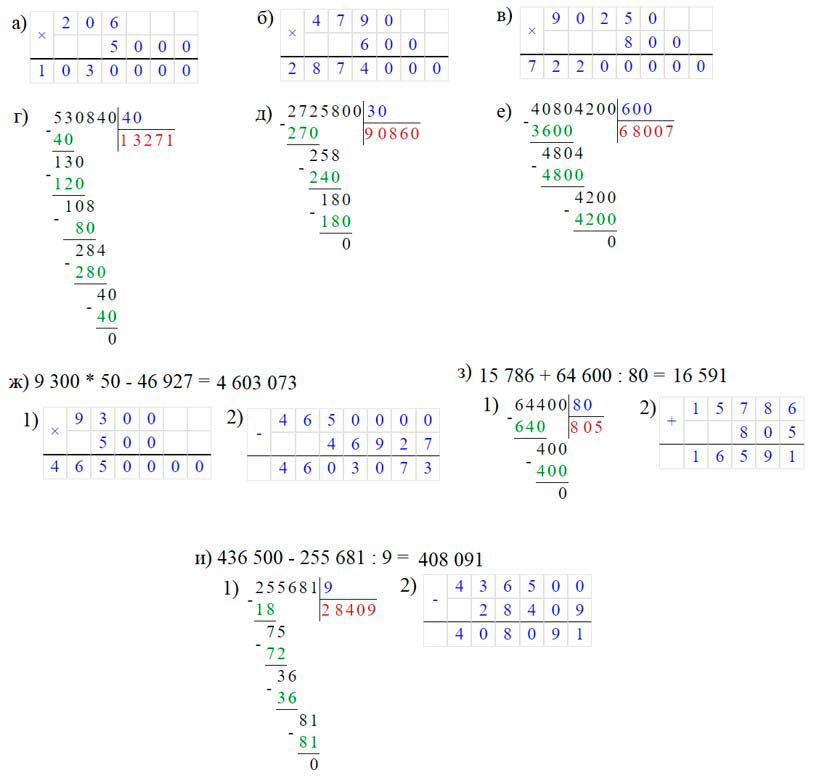
Вычисли:
а) 206 ⋅ 5 000;
б) 4 790 ⋅ 600;
в) 800 ⋅ 90 250;
г) 530 840 : 40;
д) 2 725 800 : 30;
е) 40 804 200 : 600;
ж) 9 300 ⋅ 50 – 46 927;
з) 15 786 + 64 400 : 80;
и) 436 500 – 255 681 : 9.
Номер 6.
Объясни смысл равенств: а – (b + c) = (a – b) – c = (a – c) – b.
Используя эти равенства, вычисли наиболее удобным способом:
84 – (64 + 19);
158 – (96 + 58);
349 – (5 + 249).
Чтобы из числа вычесть сумму, можно из этого числа вычесть первое число, а потом вычесть другое. Можно сначала из этого числа вычесть второе число, а потом вычесть второе.
84 – (64 + 19) = (84 – 64) – 19 = 20 – 19 = 1;
158 – (96 + 58) = (158 – 58) – 96 = 100 – 96 = 4;
349 – (5 + 249) = (349 – 249) – 5 = 100 – 5 = 95.
Номер 7.
Подбери корни уравнений и сделай проверку:
х + х = 36;
60 = а + а + а;
у + у = у + 5.
Номер 8.
Сравни выражения, не вычисляя. Обоснуй свой ответ.
60 705 + 124 … 124 + 60 705 и 10 735 : 113 … 10 735 : 5;
64 ⋅ 308 … 308 ⋅ 64 и 2 089 – 916 … 3 000 - 916;
756 ⋅ 32 … 28 ⋅ 736 и (36 + 29) ⋅ 6 … 36 ⋅ 6 + 29 ⋅ 6;
3 094 – 86 … 3 094 – 806 и (56 + 4) ⋅ 2 … 56 + 4 ⋅ 2.
60 705 + 124 = 124 + 60 705, потому что от перестановки мест слагаемых значение суммы не изменяется;
10 735 : 113 < 10 735 : 5, потому что при делении одного и того же числа на части, больше значение частного там, где делитель меньше;
64 ⋅ 308 = 308 ⋅ 64, потому что от перестановки мест множителей значение произведения не изменяется;
2 089 – 916 < 3 000 – 916, потому что при вычитании одного и того же числа, значение разности больше там, где уменьшаемое больше;
756 ⋅ 32 > 28 ⋅ 736, потому что один из множителей больше, а 32 > 28;
(36 + 29) ⋅ 6 = 36 ⋅ 6 + 29 ⋅ 6, по распределительному свойству умножения относительно сложения
3 094 – 86 > 3 094 – 806, потому что из одного и того же числа вычли разные числа, а значение разности больше там, где вычитаемое меньше;
(56 + 4) ⋅ 2 < 56 + 4 ⋅ 2, потому что в первом случае применяется распределительное свойство умножения относительно сложения.
Напишите свой комментарий.