Математика 3 класс учебник Петерсон 1 часть ответы – страница 31

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 1.
- Год: 2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Урок 11
Свойства пересечения множеств*
Номер 1.
а) Назови записанные свойства сложения и умножения. В чём их смысл?

б) Обладают ли этими свойствами вычитание и деление? Обоснуй свой ответ.
Ответ:а) Сложение – это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число. Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми. Слагаемые – это числа, единицы которых складываются. Сумма – это число, которое получается в результате сложения. Переместительное свойство сложения. От перестановки мест слагаемых сумма не меняется. a + b = b + a Сочетательное свойство сложения. Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа. (a + b) + c = a + (b + c) Умножение – это повторение, складывание одинаковых чисел (умножение заменяет неоднократно повторенное сложение). Компоненты произведения – первый множитель, второй множитель, произведение. Первое число (первый множитель) повторяют несколько раз, а сколько именно раз – показывает второе число (второй множитель). Результат умножения – произведение. Умножение натуральных чисел и его свойства. Переместительное свойство умножения: а · b = b · a. Сочетательное свойство умножения: а · (b · с) = (a · b) · с б) При вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого. Разность показывает на сколько больше уменьшаемое больше вычитаемого. При делении любого числа на 1 получается это же число: а : 1 = а При делении числа на это же число, получается единица: а : а = 1. Поэтому не обладают этими свойствами вычитание и деление.
Номер 2.
А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества А ∩ В и В ∩ А. Покажи их на диаграмме Эйлера–Венна. Что ты замечаешь? А ∩ В = ... B ∩ A = ...
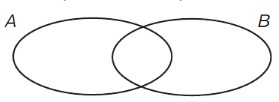
Сделай вывод.
Ответ: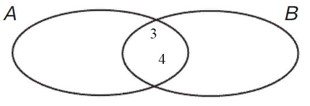
А ∩ В = {3; 4} B ∩ A = {3; 4} А ∩ В = B ∩ A Заметно что эти множества имеют одни и те же элементы.
Номер 3.
Нарисуй диаграмму множеств А, В и С. Закрась на ней сначала А ∩ В, потом С, а затем обведи их пересечение (А ∩ В) ∩ C. Аналогично построй диаграмму множества А ∩ (В ∩ C).
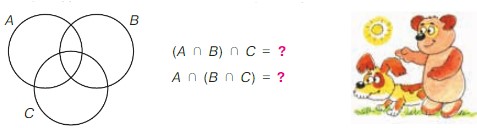
Сравни полученные множества. Что ты замечаешь? Сделай вывод.
Ответ: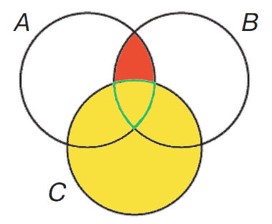
(А ∩ В) ∩ C
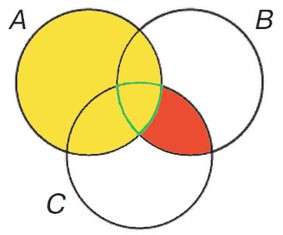
А ∩ В = {3; 4} B ∩ A = {3; 4} А ∩ В = B ∩ A Заметно что эти множества имеют одни и те же элементы.
Пересечение множеств обладает переместительным и сочетательным свойствами.
Переместительное свойство: А ∩ В = В ∩ А
Сочетательное свойство: (А ∩ В) ∩ C = А ∩ (В ∩ C)
Значит, результат пересечения множеств не зависит от порядка множеств и от порядка действий.
Номер 4.
Допиши в тетради равенства, выражающие свойства пересечения множеств. Назови эти свойства и объясни их смысл. М ∩ К = ... (М ∩ К) ∩ Т = ...
Ответ:М ∩ К = множество К в множестве М (М ∩ К) ∩ Т = М ∩ К в множестве Т
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.