Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 79

Учебник 2 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 2.
Год: 2021-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Математика 2 часть. 3 класс - Учебник. Моро. Страница 79. Год 2024

Номер 15.

Отличается задание? Переключите год учебника.

2021 2023

Начерти в тетради такие фигуры и найди площадь каждой части, закрашенной:
1) желтым цветом; 2) синим цветом.

математика 3 класс учебник 2 часть Моро страница 8.

Ответ:

1) 1см², 8 см², 4 см². 2) 3см², 4 см², 2 см².

Подсказка:

1) Площадь фигуры – часть плоскости, которая ограничена линией и которую, занимает фигура.

2) Ось симметрии – линия, по которой можно сложить фигуру так, что части совпадут при перегибании, т.е. наложении.

Рассмотрим первую фигуру.

Шаг 1.
Начертим фигуру.

Начертим квадрат со стороной 2 см и внутри него квадрат со стороной 1 см.

Шаг 2.
Рассуждаем.

Найдём площадь части, закрашенную жёлтым цветом.

Желтая часть – это квадрат со стороной 1 см. Чтобы найти площадь квадрата нужно длину умножить на ширину, а стороны у квадрата равны.

1 см ∙ 1 см = 1 (см²) – площадь желтой фигуры.

Шаг 3.
Продолжаем рассуждение.

Вычислим площадь части, закрашенную синем цветом.

1) Вначале узнаем площадь всего квадрата со стороной 2 см.

2 ∙ 2 = 4 (см²) – площадь всей фигуры.

2) Площадь всей фигуры складывается из площади желтой и синей фигур. Чтобы найти площадь синей фигуры из площади всей фигуры вычтем площадь жёлтой фигуры.

4 – 1 = 3 (см²) – площадь синей фигуры.

Шаг 4.
Отвечаем на вопрос.

У данной фигуры 4 оси симметрии: горизонтальная, вертикальная и две диагональных.

Значит, данную фигуру можно назвать симметричной.

Рассмотрим вторую фигуру.

Шаг 1.
Начертим фигуру.

Начертим прямоугольник со сторонами 4 см и 3 см. Внутри прямоугольника начертим по бокам 4 квадрата со стороной 1 см.

Шаг 2.
Рассуждаем.

Найдём площадь части, закрашенной синим цветом.

1) Синяя часть состоит из четырех одинаковых квадратов со стороной 2 см. Чтобы найти площадь одного такого квадрата нужно длину умножить на ширину, но у квадрата длина равна ширине.

1 ∙ 1 = 1 (см²) – площадь 1 синего квадрата.

2) Таких квадратов 4. Значит, площадь одного такого квадрата умножим на 4.

1 ∙ 4 = 4 (см²) – площадь синей части.

Шаг 3.
Продолжаем рассуждение.

Найдём площадь жёлтой части.

1) Вначале узнаем площадь всего прямоугольника со сторонами 4 см и 3 см. Для этого умножим длину на ширину.

4 см ∙ 3 см = 12 (см²) – площадь всего прямоугольника.

2) Площадь всей фигуры складывается из площади желтой и синей фигур. Чтобы найти площадь жёлтой фигуры из площади всей фигуры вычтем площадь синей фигуры.

12 – 4 = 8 (см²) – площадь желтой части.

Шаг 4.
Отвечаем на вопрос.

Данная фигура имеет две оси симметрии: горизонтальная и вертикальная.

Значит, данную фигуру можно назвать симметричной.

Рассмотрим третью фигуру.

Шаг 1.
Начертим фигуру.

Начертим прямоугольник со сторонами 3 см и 2 см. Разделим его на квадрат со стороной 2 см и прямоугольник со сторонами 1 см и 2 см.

Шаг 2.
Рассуждаем.

Найдём площадь жёлтой части.

Жёлтая часть – это квадрат со стороной 2 см. Чтобы найти площадь квадрата нужно длину умножить на ширину, но у квадрата длина равна ширине.

2 см ∙ 2 см = 4 (см²) – площадь жёлтой части.

Шаг 3.
Продолжаем рассуждение.

Найдём площадь синей части.

Синяя часть – это прямоугольник со сторонами 1 см и 2 см. Чтобы найти площадь умножим длину на ширину.

1 см ∙ 2 см = 2 (см²) – площадь синей части.

Шаг 4.
Отвечаем на вопрос.

Данная фигура имеет одну ось симметрии – горизонтальную.

Значит, данную фигуру можно назвать симметричной.

Оформляем задание в тетрадь.

Шаг 1.
Начертим фигуры.

Шаг 2.
Задание 1.

Площадь жёлтой части.

Фигура 1:
1 см ∙ 1 см = 1 см² – площадь желтой части.

Фигура 2:
4 см ∙ 3 см = 12 см² – площадь всего прямоугольника.
1 см ∙ 1 см = 1см² – площадь 1 синего квадрата.
1 см² ∙ 4 = 4 см² – площадь синей части.
12 см² – 4 см² = 8 см² – площадь желтой части.

Фигура 3:
2 см ∙ 2 см = 4 см² – площадь жёлтой части.

Ответ: 1 см²; 8 см²; 4 см².

Шаг 3.
Задание 2.

Площадь синей части.

Фигура 1:
2 см ∙ 2 см = 4 см² – площадь всего квадрата.
4 – 1 = 3 см² – площадь синей части.

Фигура 2:
1 см ∙ 1 см = 1 см² – площадь 1 синего квадрата.
1 см² ∙ 4 = 4 см² – площадь синей части.

Фигура 3:
1 см ∙ 2 см = 2 см² – площадь синей части.

Шаг 4.
Отвечаем на вопрос.

Ответ: да, каждую фигуру можно назвать симметричной.

Начерти в тетради такие фигуры и найди площадь каждой части, закрашенной:
1) желтым цветом; 2) синим цветом.
Можно ли каждую фигуру назвать симметричной?

Ответ:

1) 1см², 8 см², 4 см². 2) 3см², 4 см², 2 см².
Нет, так как третья фигура не симметрична по вертикали.

Номер 16.

В саду посадили 96 яблонь, а слив на 64 дерева меньше. Во сколько раз больше посадили яблонь, чем слив?

Ответ:

математика 3 класс учебник 2 часть Моро страница 79. Номер 16

1) 96 – 64 = 32 (с.) – посадили. 2) 96 : 32 = 3 - раза больше.
Ответ: посадили в 3 раза больше яблонь, чем слив.

Подсказка:

1) «Во сколько раз» вычисляется делением.
2) «На меньше» вычисляется вычитанием.

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
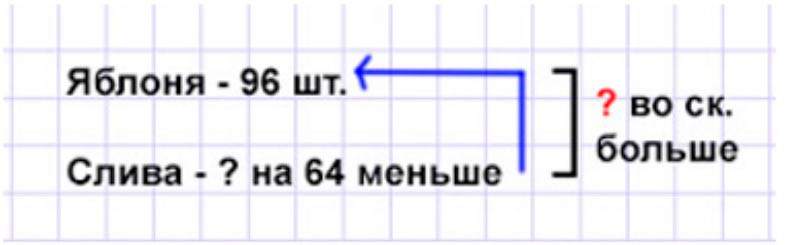
Рассуждаем.

Яблонь посадили 96, а слив на 64 дерева меньше. На 64 меньше – это столько же, но минус 64.

96 – 64 = (90 – 60) + (6 – 4) = 30 + 2 =32 (дер.) – просадили слив.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.

96 : 32 = 3 (раз) – во столько раз больше яблонь больше, чем слив.

Шаг 4.
Записываем ответ.

Ответ: в 3 раза.

Решение выражением:
96 : (96 – 64) = 3 (раза) – на сколько больше,
где 96 – 64 – количество посаженных слив.

Номер 17.

Ответ:

84 : 12 = 7 42 ∙ 2 – 42 = 42 54 : 18 = 3 4 ∙ 15 + 15 = 75 78 : 26 = 3 6 ∙ 13 – 13 = 65
80 : (4 + 76) = 1 56 : 8 ∙ 7 = 49 96 – 64 : 4 = 80 63 : 9 ∙ 5 = 35 (96 − 64) : 4 = 8 70 : 10 = 7

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.

4) Вспомни как найти деление методом подбора.

Шаг 1.
Рассуждаем и выполняем вычисления.

Выполним деление методом подбора.

84 : 12 = ?
Пробуем в частном 6 и проверяем: 12 ∙ 6 = 72, 72 < 84, число 6 не подходит.
Пробуем в частном 7 и проверяем: 12 ∙ 7 = 84, 84 = 84, значит 84 : 12 = 7.
Ответ: 7.

54 : 18 = ?
Пробуем в частном 2 и проверяем: 18 ∙ 2 = 36, 36 < 54, число 2 не подходит.
Пробуем в частном 3 и проверяем: 18 ∙ 3 = 54, 54 = 54, значит 54 : 18 = 3.
Ответ: 3.

78 : 26 = ?
Пробуем в частном 2 и проверяем: 26 ∙ 2 = 52, 52 < 78, число 2 не подходит.
Пробуем в частном 3 и проверяем: 26 ∙ 3 = 78, 78 = 78, значит 78 : 26 = 3.
Ответ: 3.

Выполним вычисления по действиям.

1 2
42 · 2 − 42 = 42
1) 42 ∙ 2 = (40 + 2) ∙ 2 = 80 + 4 = 84
2) 84 − 42 = (80 − 40) + (4 − 2) = 40 + 2 = 42

1 2
4 · 15 + 15 = 75
1) 4 ∙ 15 = 4 ∙ (10 + 5) = 40 + 20 = 60
2) 60 + 15 = (60 + 10) + 5 = 70 + 5 = 75

1 2
6 ∙ 13 − 13 = 65
1) 6 ∙ 13 = 6 ∙ (10 + 3) = 60 + 18 = 78
2) 78 − 13 = (70 − 10) + (8 − 3) = 60 + 5 = 65

2 1
80 : (4 + 76) = 1
1) 4 + 76 = 70 + (4 + 6) = 70 + 10 = 80
2) 80 : 80 = 1

2 1
96 − 64 : 4 = 80
1) 64 : 4 = (40 + 24) : 4 = 10 + 6 = 16
2) 96 − 16 = (90 − 10) + (6 − 6) = 80 + 0 = 80

1 2
(96 − 64) : 4 = 8
1) 96 – 64 = (90 – 60) + (6 – 4) = 30 + 2 = 32
2) 32 : 4 = 8

1 2
56 : 8 ∙ 7 = 49
1) 56 : 8 = 7
2) 7 ∙ 7 = 49

1 2
63 : 9 ∙ 5 = 35
1) 63 : 9 = 7
2) 7 ∙ 5 = 35

70 : 10 = 7 дес. : 1 дес. = 7

Шаг 2.
Оформляем задание в тетрадь.

84 : 12 = 7, так как 12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84

54 : 18 = 3, так как 18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54

78 : 26 = 3, так как 26 ∙ 3 = (20 + 6) ∙ 3 = 60 + 18 = 78

42 ∙ 2 − 42 = 84 − 42 = 42
4 ∙ 15 + 15 = 60 + 15 = 75
6 ∙ 13 − 13 = 78 − 13 = 65
80 : (4 + 76) = 80 : 80 = 1
96 − 64 : 4 = 96 – 16 = 80
(96 − 64) : 4 = 32 : 4 = 8
56 : 8 ∙ 7 = 7 ∙ 7 = 49
63 : 9 ∙ 5 = 7 ∙ 5 = 35
70 : 10 = 7

Номер 18.

Ответ:

6 см 8 мм < 7 см 2 мм 8 дм 2 см > 6 дм 8 см
9 м 5 дм > 9 м 5 см 400 см > 4 дм

Подсказка:

1) Помни, что сравнивать можно только числовые значения длины, выраженные в одних единицах измерения.
2) Помни, что 1 м = 100 см, 1 см = 10 мм.

Шаг 1.
Выполняем вычисления с пояснениями.

Переведем все значения в одни единицы измерения, например, в сантиметры или миллиметры и сравним результаты.

Сравним 6 см 8 мм и 7 см 2 мм,
6 см 8 мм = 60 мм + 8 мм = 68 мм
7 см 2 мм = 70 мм + 2 мм = 72 мм
68 мм < 72 мм, значит 6 см 8 мм < 7 см 2 мм.

Сравним 8 дм 2 см и 6 дм 8 см,
8 дм 2 см = 80 см + 2 см = 82 см
6 дм 8 см = 60 см + 8 см = 68 см
82 см > 68 см, значит 8 дм 2 см > 6 дм 8 см.

Сравним 9 м 5 дм и 9 м 5 см,
9 м 5 дм = 9 м 50 см
9 м 50 см > 9 м 5 см, значит 9 м 5 дм > 9 м 5 см.

Сравним 400 см и 4 дм,
4 дм = 4 ∙ 10 см = 40 см
400 см > 40 см, значит 400 см > 4 дм.

Шаг 2.
Оформляем задание в тетрадь.

6 см 8 мм < 7 см 2 мм, так как 6 см < 7 см

8 дм 2 см > 6 дм 8 см, так как 8 дм > 6 дм

9 м 5 дм > 9 м 5 см, так как 50 см > 5 см

400 см > 4 дм, так как 400 см > 40 см

Номер 19.

Ответ:

1000 – 400 ∙ 2 = 1000 - 800 = 200 80 : 2 + 600 = 40 + 600 = 640 30 : 6 ∙ 20 = 5 * 20 = 100
(700 + 13) + 200 = 900 + 13 = 913 (800 + 47) – 500 = 300 + 47 = 347 (400 + 68) + 300 = 700 + 68 = 768
(170 − 110) : 5 = 60 : 5 = 12 (100 − 8) : 4 = 92 : 4 = 23 84 : (230 − 218) = 84 : 12 = 7

Подсказка:

Шаг 1.
Рассуждаем и выполняем вычисления.

2 1
1000 − 400 · 2 = 200
1) 400 ∙ 2 = 4 сот. ∙ 2 = 8 сот. = 800
2) 1000 − 800 = 10 сот. − 8 сот. = 2 сот. = 200

1 2
80 : 2 + 600 = 640
1) 80 : 2 = 8 дес. : 2 = 4 дес. = 40
2) 40 + 600 = 4 дес. + 60 дес. = 64 дес. = 640

1 2
30 : 6 ∙ 20 = 100
1) 30 : 6 = 5
2) 5 ∙ 20 = 5 ∙ 2 дес. = 10 дес. = 100

1 2
(700 + 13) + 200 = 913
1) 700 + 13 = 713
2) 713 + 200 = (700 + 13) + 200 = (700 + 200) + 13 = 900 + 13 = 913

1 2
(800 + 47) − 500 = 347
1) 800 + 47 = 847
2) 847 − 500 = (800 + 47) − 500 = (800 − 500) + 47 = 300 + 47 = 347

1 2
(400 + 68) + 300 = 768
1) 400 + 68 = 468
2) 468 + 300 = (400 + 68) + 300 = (400 + 300) + 68 = 700 + 68 = 768

1 2
(170 − 110) : 5 = 12
1) 170 − 110 = 60
2) 60 : 5 = (50 + 10) : 5 = 10 + 2 = 12

1 2
(100 − 8) : 4 = 23
1) 100 – 8 = 92
2) 92 : 4 = (80 + 12 ) : 4 = 20 + 3 = 23

2 1
84 : (230 − 218) = 7
1) 230 – 218 = 12
2) 84 : 12 = 7

Шаг 2.
Оформляем задание в тетрадь.

1000 − 400 ∙ 2 = 1000 − 800 = 200
80 : 2 + 600 = 40 + 600 = 640
30 : 6 ∙ 20 = 5 ∙ 20 = 100
(700 + 13) + 200 = 713 + 200 = 913
(800 + 47) − 500 = 847 − 500 = 347
(400 + 68) + 300 = 468 + 300 = 768
(170 − 110) : 5 = 50 : 5 = 12
(100 − 8) : 4 = 92 : 4 = 23
84 : (230 − 218) = 84 : 12 = 7

Номер 20.

Не вычисляя, скажи, в каком уравнении каждой пары значение х будет больше.
Проверь, решив уранения.

Ответ:

x + 25 = 40 x + 25 = 60
Больше будет значение X во втором уравнении, потому что второе слагаемое в первом и втором уравнении одинаково, а сумма второго больше суммы первого. x + 25 = 40 x + 25 = 60 x = 40 − 25 x = 60 − 25 x = 15 x = 35

x − 28 = 50 x − 28 = 49
Больше будет значение X в первом уравнении, потому что вычитаемые равны, а в разности различны. Чем больше уменьшаемое, тем разность больше. x − 28 = 50 x − 28 = 49 x = 50 + 28 x = 28 + 49 x = 78 x = 77

90 − x = 42 90 − x = 52 Больше будет значение X в первом уравнении, потому что уменьшаемые равны, а разность в первом меньше, чем разность во втором уравнении.
90 − x = 42 90 − x = 52 x = 90 − 42 x = 90 − 52 x = 48 x = 38

x ∙ 3 = 84 x ∙ 3 = 72
Значение X будет больше в первом уравнении, потому что чем больше произведение при одном и том же множителе, тем большим будет второй множитель. x ∙ 3 = 84 x ∙ 3 = 72 x = 84 : 3 x = 72 : 3 x = 28 x = 24

x : 5 = 9 x : 5 = 11
Значение X будет больше во втором уравнении, потому что чем больше частное, получаемое при делении числа на один и тот же делитель, тем больше делимое. x : 5 = 9 x : 5 = 11 x = 5 ∙ 9 x = 5 ∙ 11 x = 45 x = 55

96 : x = 6 96 : x = 4
Потому что при делении одного и того же числа частное будет больше, если делитель будет меньше. 96 : x = 6 96 : x = 4 x = 96 : 6 x = 96 : 4 x = 16 x = 24

Подсказка:

Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.

Шаг 1.
Рассуждаем.

Сравним уравнения.

1 пара:
х + 25 = 40 и х + 25 = 60
х – неизвестное слагаемое.
Вторые слагаемые в первом и втором уравнении одинаковы. Значит неизвестное слагаемое больше в том уравнении, в котором больше сумма.

Сумма в первом уравнении – 40.
Сумма во втором уравнении – 60.
40 < 60 – сумма во 2 уравнении больше, чем в 1 уравнении, значит неизвестное во втором уравнении больше.

Ответ: х больше во 2 уравнении.

2 пара:
x − 28 = 50 и x − 28 = 49
х – неизвестное уменьшаемое.
В данных уравнениях вычитаемые равны. Значит, неизвестное уменьшаемое больше в том уравнении, в котором разность больше.

Разность в первом уравнении – 50.
Разность во втором уравнении – 49.
50 > 49 – разность в 1 уравнении больше, чем во 2 уравнении, значит неизвестное в первом уравнении больше.

Ответ: х больше в 1 уравнении.

3 пара:
90 − x = 42 и 90 − x = 52
х – неизвестное вычитаемое.
В данных уравнениях уменьшаемые равны. Значит, неизвестное вычитаемое больше в том уравнении, где разность будет меньше.

Разность в первом уравнении – 42.
Разность во втором уравнении – 52.
42 < 52 – разность в 1 уравнении меньше, значит вычитаемое будет больше.

Ответ: х больше в 1 уравнении.

4 пара:
x ∙ 3 = 84 и x ∙ 3 = 72
х – неизвестный множитель.
Второй множитель у первого и второго уравнения равны. Значит неизвестный множитель больше в том уравнении, где произволение больше.

Произведение в первом уравнении – 84.
Произведение во втором уравнении – 72.
84 > 72 – произведение в 1 уравнении больше, чем во 2 уравнении, значит неизвестный множитель в 1 уравнении больше.

Ответ: х больше в 1 уравнении.

5 пара:
x : 5 = 9 и x : 5 = 11
х – неизвестное делимое.
В данных уравнениях делители одинаковы. Значит делимое будет больше в том уравнении у которого частное больше.

Частное в первом уравнении – 9.
Частное во втором уравнении – 11.
9 < 11 – частное во 2 уравнении больше, чем в 1 уравнении, значит неизвестное делимое больше во 2 уравнении.

Ответ: х больше во 2 уравнении.

6 пара:
96 : x = 6 и 96 : x = 4
х – неизвестный делитель.
Делимые в обоих уравнениях одинаковы. Значит, делитель больше в том уравнении, в котором частное меньше.

Частное в первом уравнении – 6.
Частное во втором уравнении – 4.
6 > 4 – частное во 2 уравнении меньше, значит делитель будет больше.

Ответ: х больше во 2 уравнении.

Шаг 2.
Делаем проверку.

Во втором уравнении неизвестное больше.

В первом уравнении неизвестное больше.

Во втором уравнении неизвестное больше.

Шаг 3.
Оформляем задание в тетрадь.

1) х + 25 = 40 и х + 25 = 60

x − 28 = 50 и x − 28 = 49

90 − x = 42 и 90 − x = 52

2) x ∙ 3 = 84 и x ∙ 3 = 72

x : 5 = 9 и x : 5 = 11

96 : x = 6 и 96 : x = 4

Номер 21.

В большую бочку входит ☐ ведер воды, а в маленькую – в 3 раза меньше. Из каждой бочки взяли по 3 ведра воды. Дополни условие и составь по нему различные выражения.

Ответ:

12 : 3 – вёдер воды в маленькой бочке. 12 – 3 – осталось вёдер воды в большой бочке. 12 : 3 – 3 – осталось вёдер воды в маленькой бочке. 12 : 3 + 12 – вёдер воды в двух бочках. (12 : 3 – 3) + (12 – 3) – осталось вёдер воды в двух бочках.

Подсказка:

1) «В 3 раза меньше», значит, разделить на 3, т.е. вычисляется делением.
2) Внимательно прочитай задачу и составь выражения.

Задача 1.

В большую бочку входит 18 ведер воды, а в маленькую – в 3 раза меньше. Из каждой бочки взяли по 3 ведра воды.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Если в количество воды большой бочки разделить на 3, то узнаем сколько ведер воды входит в маленькую бочку.

18 : 3 = 6 (в.) – в маленькой бочке.

Шаг 3.
Продолжаем рассуждение.

Если из количества воды в большой бочке вычесть количество воды, которую взяли, то узнаем сколько воды останется в большой бочке.

18 – 3 = 15 (в.) – осталось воды в большой бочке.

Шаг 4.
Продолжаем рассуждение.

Если из количества воды в маленькой бочке вычесть количество воды, которую взяли, то узнаем сколько воды останется в маленькой бочке.

18 : 3 – 3 = 3 (в.) – осталось воды в маленькой бочке.
1) 18 : 3 = 6
2) 6 – 3 = 3

Шаг 5.
Продолжаем рассуждение.

Общее количество воды в двух бочках складывается из воды в большой и маленькой бочках.

18 : 3 + 18 = 24 (в.) – воды в двух бочках.
1) 18 : 3 = 6
2) 6 + 18 = 24

Шаг 6.
Продолжаем рассуждение.

Чтобы узнать сколько осталось воды в двух бочках, нужно сложить два остатка воды из каждой бочки.

(18 : 3 – 3) + (18 – 3) = 18 (в.) – осталось воды в двух бочках.
1) 18 : 3 = 6
2) 6 – 3 = 3
3) 18 – 3 = 15
4) 3 + 15 = 18

Шаг 7.
Оформляем задание в тетрадь.

1) 18 : 3 = 6 (в.) – в маленькой бочке.

2) 18 – 3 = 15 (в.) – осталось воды в большой бочке.

3) 18 : 3 – 3 = 6 – 3 = 3 (в.) – осталось воды в маленькой бочке.

4) 18 : 3 + 18 = 6 + 18 = 24 (в.) – воды в двух бочках.

5) (18 : 3 – 3) + (18 – 3) = (6 – 3) + 15 = 3 + 15 = 18 (в.) – осталось воды в двух бочках.

Задание на полях страницы

Продолжи ряды чисел:

Ответ:

16 → 28 20 → 35 24 → 42 28 → 49 32 → 56 36 → 63 40 → 70
Пояснение:
16 : 4 ∙ 7 = 28 20 : 4 ∙ 7 = 35 24 : 4 ∙ 7 = 42 28 : 4 ∙ 7 = 49 32 : 4 ∙ 7 = 56 36 : 4 ∙ 7 = 63 40 : 4 ∙ 7 = 70

Подсказка:

1) Для того, чтобы продолжить ряд чисел, необходимо увидеть закономерность.
2) В левом столбце записаны числа, с которыми происходят какие-то изменения, а в правом – новые уже после выполнения действий.
3) Сравни числа в обоих столбцах

Шаг 1.
Рассуждаем.

Рассмотрим числа в левом столбце.

Каждое последующее число в левом столбце на 4 больше предыдущего.

Значит числа в левом столбце:
16 – первое число
16 + 4 = 20 – второе число
20 + 4 = 24 – третье число
24 + 4 = 28 – четвертое число
28 + 4 = 32 – пятое число
32 + 4 = 36 – шестое число
36 + 4 = 40 – седьмое число

Шаг 2.
Продолжаем рассуждение.

Рассмотрим числа в правом столбце.

Число, которое стоит в левом столбце умножают на само себя и к результату прибавляют 3 и получается число, стоящее в правом столбце.

Схема ряда выглядит так: х : 4 ∙ 7, где х – число которое стоит в левом столбце.

Шаг 3.
Выполняем вычисления.

16 : 4 ∙ 7 = 4 ∙ 7 = 28
20 : 4 ∙ 7 = 5 ∙ 7 = 35
24 : 4 ∙ 7 = 6 ∙ 7 = 42
28 : 4 ∙ 7 = 7 ∙ 7 = 49
32 : 4 ∙ 7 = 8 ∙ 7 = 56
36 : 4 ∙ 7 = 9 ∙ 7 = 63
40 : 4 ∙ 7 = 10 ∙ 7 = 70

Шаг 4.
Оформляем задание в тетрадь.

16 → 28
20 → 35
24 → 42
28 → 49
32 → 56
36 → 63
40 → 70

Конец страницы