Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 43

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Сколько всего палочек, если взяли:
1) 2 пучка по 100 палочек, 4 пучка по 10 палочек и 5 палочек; 2) 5 пучков по 100 палочек и 7 палочек?
Ответ:1) 200 палочек, 45 палочек. 2) 507 палочек.
Вспомни как образуются и называются трёхзначные числа.
Оформляем задание в виде рисунка.
.jpg)
Рассуждаем.
2 пучка по 100 палочек: 2 ∙ 100 = 2 ∙ 1 сот. = 2 сот. = 200
4 пучка по 10 палочек: 4 ∙ 10 = 4 ∙ 1 дес. = 4 дес. = 40
5 палочек: 5 единиц.
200 + 40 + 5 = 245 палочек.
Оформляем задание в тетрадь.
.jpg)
Ответ: 245 палочек.
Оформляем задание в виде рисунка.
.jpg)
Рассуждаем.
5 пучков по 100 палочек: 5 ∙ 100 = 5 ∙ 1 сот. = 5 сот. = 500
7 палочек: 7 единиц.
500 + 7 = 507 палочек.
Оформляем задание в тетрадь.
.jpg)
Ответ: 507 палочек.
Номер 2.
Как с помощью палочек изобразить числа: двести тридцать шесть? триста пять? восемьсот?
Ответ:236 – 2 пучка по 100 палочек, 3 пучка по 10 палочек и 6 палочек. 305 – 3 пучка по 100 палочек и 5 палочек. 800 – 8 пучков по 100 палочек.
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
1) Двести тридцать шесть:
236 = 2 сот. + 3 дес. + 6 ед. = 2 ∙ 100 + 3 ∙ 10 + 6
2 сот. = 2 ∙ 100
3 дес. = 3 ∙ 10
6 ед. = 6
2) Триста пять:
305 = 3 сот. + 0 дес. + 5 ед. = 3 ∙ 100 + 5
3 сот. = 3 ∙ 100
5 ед. = 5
800 = 8 сот. + 0 дес. + 0 ед.= 8 ∙ 100
8 сот. = 8 ∙ 100
Оформляем задание в виде рисунка.
.jpg)
Оформляем задание в тетрадь.
.jpg)
Ответ: 236 – 2 пучка по 100 палочек, 3 пучка по 10 палочек и 6 палочек.
.jpg)
Ответ: 305 – 3 пучка по 100 палочек и 5 палочек.
.jpg)
Ответ: 800 – 8 пучков по 100 палочек.
Номер 3.
Назови число, которое содержит:
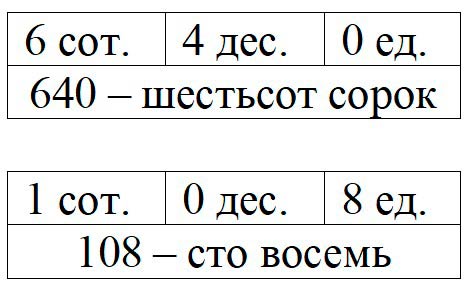
6 сот. 4 дес. 0 ед. 1 сот. о дес. 8 ед.
Ответ:640 108
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
6 сот. 4 дес. 0 ед. = 6 ∙ 1 сот. + 4 ∙ 1 дес. + 0 ед. = 6 ∙ 100 + 4 ∙ 10 + 0 = 600 + 40 + 0 = 640
1 сот. 0 дес. 8 ед. = 1 ∙ 100 + 0 ∙ 10 + 8 = 100 + 0 + 8 = 108
Оформляем задание в тетрадь.
Номер 4.
Грузовая машина расходует за 1 ч работы 15 л горючего. На сколько часов работы хватит 45 л горючего? 60 л? 90 л?
Ответ:
1) 45 : 15 = 3 (ч) работы хватит 45 л горючего. 2) 60 : 15 = 4 (ч) работы хватит 60 л горючего. 3) 90 : 15 = 6 (ч) работы хватит 90 л горючего. Ответ: на 3 ч работы хватит 45 л горючего, на 4 ч хватит 60 литров горючего, на 6 ч хватит 90 литров горючего.
Данная задача вида «Расход горючего за 1 час, количество горючего, время» характеризуется зависимостями между элементами:
Расход за 1 час ∙ время = количество горючего.
Количество горючего : время = расход за 1 час.
Количество горючего : расход за 1 час = количество горючего.
Оформляем задание в виде таблицы.
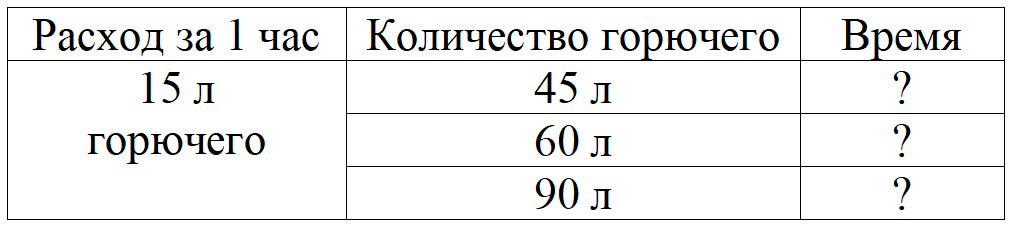
Рассуждаем.
За каждый час работы грузовая машина расходует 15 литров горючего. Значит, каждый час она расходует одинаковое количество горючего.
Чтобы узнать на сколько времени хватит определенного количества горючего нужно общее количество горючего разделить на расход за 1 час.
1) 45 : 15 = 3 (ч) – хватит 45 л горючего;
Вычислим методом подбора:
Пробуем в частном 2 и проверяем: 15 ∙ 2 = 30, 30 < 45, число 2 не подходит.
Пробуем в частном 3 и проверяем: 15 ∙ 3 = 45, 45 = 45, значит 45 : 15 = 3.
2) 60 : 15 = 4 (ч) – хватит 60 л горючего;
Вычислим методом подбора:
Пробуем в частном 4 и проверяем: 15 ∙ 4 = (10 + 5) ∙ 4 = 40 + 20 = 60, 60 = 60, значит 60 : 15 = 4.
3) 90 : 15 = 6 (ч) – хватит 90 л горючего.
Вычислим методом подбора:
Пробуем в частном 5 и проверяем: 15 ∙ 5 = (10 + 5) ∙ 5 = 50 + 25 = 75, 75 < 90, число 5 не подходит.
Пробуем в частном 6 и проверяем: 15 ∙ 6 = (10 + 5) ∙ 6 = 60 + 30 = 90, 90 = 90, значит 90 : 15 = 6.
Записываем ответ.
Ответ: 45 л горючего хватит на 3 часа;
60 л горючего – на 4 часа;
90 л горючего – на 6 часов.
Номер 5.
Грузовая машина при перевозке мебели израсходовала до остановки 48 л горючего, а после остановки 32 л. Сколько часов была в пути машина, если за 1 ч расходовалось 16 л горючего?
Ответ:
1-й способ решения:
1) 48 + 32 = 80 (л) – горючего израсходовано.
2) 80 : 16 = 5 (ч) – машина была в пути.
Ответ: машина была в пути всего 5 часов.
2-й способ решения:
1) 48 : 16 = 3 (ч) – время до остановки
2) 32 : 16 = 2 (ч) – время после остановки
3) 3 + 2 = 5 (ч) – были в пути
Ответ: 5 часов.
3-й способ решения:
(48 + 32) : 16 = 80 : 16 = 5 (ч) – в пути
или
48 : 16 + 32 : 16 = 3 + 2 = 5 (ч) – в пути
Ответ: 5 часов.
1) Чтобы разделить сумму на число можно вычислить сумму и разделить её на число;
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Оформляем задание в виде таблицы.

Рассуждаем.
Общий расход горючего складывается из количества, израсходованного горючего до остановки и после.
48 + 32 = 80 (л) – израсходовали всего горючего.
Продолжаем рассуждение.
Расход за 1 час составляет 16 литров горючего. Значит, каждый час расходуется одинаковое количество горючего.
Чтобы узнать время нужно общий расход горючего разделить на расход горючего за 1 час.
80 : 16 = 5 (ч) – время в пути.
Записываем ответ.
Ответ: 5 часов.
Решение выражением:
(48 + 32) : 16 = 5 часов – время в пути, где 48 + 50 – общий расход горючего.
Рассуждаем.
Расход за 1 час составляет 16 литров горючего. Значит, каждый час расходуется одинаковое количество горючего.
Чтобы узнать время нужно расход горючего разделить на расход горючего за 1 час.
48 : 16 = 3 (ч) – время до остановки.
32 : 16 = 2 (ч) – время после остановки.
Продолжаем рассуждение.
Общее время складывается из времени, которое проехала грузовая машина до остановки и после остановки.
3 + 2 = 5 (ч) – время в пути.
Записываем ответ.
Ответ: 5 часов.
Решение выражением:
48 : 16 + 32 : 16 = 5 часов – время в пути,
где 48 : 16 – время в пути до остановки,
32 : 16 – время в пути после остановки.
Номер 6.
Ответ:44 : 2 = 22 44 : 22 = 2 66 : 3 = 22 66 : 33 = 2 88 : 2 = 44 88 : 22 = 4 88 : 4 = 22 88 : 44 = 2 66 : 2 = 33 66 : 22 = 3
1) Вспомни как найти деление методом подбора.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Выполняем деление и рассуждаем.
44 : 2 = (40 + 4) : 2 = 40 : 2 + 4 : 2 = 20 + 2 = 22
Представим число 44 в виде суммы чисел 40 и 4, каждое слагаемое разделим на 2 и полученные результаты сложим.
44 : 22 = 2.
Вычислим методом подбора.
Пробуем в частном 2 и проверяем: 22 ∙ 2 = (20 + 2) ∙ 2 = 40 + 4 = 44, 44 = 44, значит 44 : 22 = 2.
66 : 3 = (60 + 6) : 3 = 60 : 3 + 6 : 3 = 20 + 2 = 22
Представим число 66 в виде суммы чисел 60 и 6, каждое слагаемое разделим на 3 и полученные результаты сложим.
66 : 33 = 2.
Вычислим методом подбора.
Пробуем в частном 2 и проверяем: 33 ∙ 2 = (30 + 3) ∙ 3 = 60 + 6 = 66, 66 = 66, значит 66 : 33 = 2.
88 : 2 = (80 + 8) : 2 = 80 : 2 + 8 : 2 = 40 + 4 = 44
Представим число 88 в виде суммы чисел 80 и 8, каждое слагаемое разделим на 2 и полученные результаты сложим.
88 : 22 = 4.
Вычислим методом подбора.
Пробуем в частном 3 и проверяем: 22 ∙ 3 = 66, 66 < 88, число 3 не подходит.
Пробуем в частном 4 и проверяем: 22 ∙ 4 = 88, 88 = 88, значит 88 : 22 = 4.
88 : 4 = (80 + 8) : 4 = 80 : 4 + 8 : 4 = 20 + 2 = 22
Представим число 88 в виде суммы чисел 80 и 8, каждое слагаемое разделим на 4 и полученные результаты сложим.
88 : 44 = 2.
Вычислим методом подбора.
Пробуем в частном 2 и проверяем: 44 ∙ 2 = (40 + 4) ∙ 2 = 80 + 8 = 88, 88 = 88, значит 88 : 44 = 2.
66 : 2 = (60 + 6) : 2 = 60 : 2 + 6 : 2 = 30 + 3 = 33
Представим число 66 в виде суммы чисел 60 и 6, каждое слагаемое разделим на 2 и полученные результаты сложим.
66 : 22 = 3.
Вычислим методом подбора.
Пробуем в частном 2 и проверяем: 22 ∙ 2 = 44, 44 < 66, число 2 не подходит.
Пробуем в частном 3 и проверяем: 22 ∙ 3 = 66, 66 = 66, значит 66 : 22 = 3.
Оформляем задание в тетрадь.
44 : 2 = (40 + 4) : 2 = 40 : 2 + 4 : 2 = 20 + 2 = 22
44 : 22 = 2, так как 22 ∙ 2 = 44
66 : 3 = (60 + 6) : 3 = 60 : 3 + 6 : 3 = 20 + 2 = 22
66 : 33 = 2, так как 33 ∙ 2 = 66
88 : 2 = (80 + 8) : 2 = 80 : 2 + 8 : 2 = 40 + 4 = 44
88 : 22 = 4, так как 22 ∙ 4 = 88
88 : 4 = (80 + 8) : 4 = 80 : 4 + 8 : 4 = 20 + 2 = 22
88 : 44 = 2, так как 44 ∙ 2 = 88
66 : 2 = (60 + 6) : 2 = 60 : 2 + 6 : 2 = 30 + 3 = 33
66 : 22 = 3, так как 22 ∙ 3 = 66
Номер 7.
Ответ:80 – 16 ∙ 5 = 80 - 80 = 0
70 + 2 ∙ 12 = 70 + 24 = 94
90 : (6 ∙ 15) = 90 : 90 = 1
68 : (72 : 18) = 68 : 4 = 17
78 : (13 − 7) ∙ 0 = 78 : 6 · 0 = 13 * 0 = 0
64 : (39 − 7) ∙ 1 = 64 : 32 · 1 = 2 * 1 = 2
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем и расставляем порядок действий.
80 − 16 ∙ 5 = 0
1) 16 ∙ 5 = (10 + 6) ∙ 5 = 50 + 30 = 80
2) 80 − 80 = 0
70 + 2 ∙ 12 = 94
1) 2 ∙ 12 = 24
2) 70 + 24 = 94
90 : (6 ∙ 15) = 1
1) 6 ∙ 15 = 6 ∙ (10 + 5) = 60 + 30 = 90
2) 90 : 90 = 1
68 : (72 : 18) = 17
1) 72 : 18 = 4 – вычисляем методом подбора
2) 68 : 4 = (40 + 28) : 4 = 10 + 7 = 17
78 : (13 − 7) ∙ 0 = 0
1) 13 − 7 = 6
2) 78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
3) 13 ∙ 0 = 0
64 : (39 − 7) ∙ 1 = 2
1) 39 − 7 = 32
2) 64 : 32 = 2
3) 2 ∙ 1 = 2
Оформляем задание в тетрадь.
80 − 16 ∙ 5 = 80 − 80 = 0
70 + 2 ∙ 12 = 70 + 24 = 94
90 : (6 ∙ 15) = 90 : 90 = 1
68 : (72 : 18) = 68 : 4 = 17
78 : (13 − 7) ∙ 0 = 78 : 6 ∙ 0 = 0
64 : (39 − 7) ∙ 1 = 64 : 32 ∙ 1 = 2
Задание внизу страницы
Назови число, которое содержит:
7 сот. 0 дес. 1 ед; 4 сот. 9 дес. 0 ед.
Ответ:7 сот. 0 дес. 1 ед. = 701 4 сот. 9 дес. 0 ед. = 490
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
7 сот. 0 дес. 1 ед. = 7 ∙ 1 сот. + 0 ∙ 1 дес. + 1 ед. = 7 ∙ 100 + 0 ∙ 10 + 1 = 700 + 0 + 1 = 701 – семьсот один
4 сот. 9 дес. 0 ед. = 4 ∙ 1 сот. + 9 ∙ 1 дес. + 0 ед. = 4 ∙ 100 + 9 ∙ 10 + 0 = 400 + 90 + 0 = 490 – четыреста девяносто
Оформляем задание в тетрадь.

Задание на полях страницы
Вычисли. Найди лишнее выражение:
28 ∙ 2 8 ∙ 7 4 ∙ 14 27 ∙ 2 56 ∙ 1
Ответ:28 ∙ 2 = 56 8 ∙ 7 = 56 4 ∙ 14 = 56 27 ∙ 2 = 54 (Лишнее выражение) 56 ∙ 1 = 56
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим выражения.
28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56
8 ∙ 7 = 56
4 ∙ 10 = 4 ∙ (10 + 4) = 40 + 16 = 56
27 ∙ 2 = (20 + 7) ∙ 2 = 40 + 14 = 54
56 ∙ 1 = 56
Делаем вывод.
Выражение 27 ∙ 2 лишнее, так как оно равно 54, а остальные равны 56.
Номер 5.
Ответ:
125 см = 100 см + 20 см + 5 см = 1 м 2 дм 5 см
86 мм = 80 мм + 6 мм = 8 см 6 мм
540 см = 500 см + 40 см = 5 м 40 см = 5 м 4 дм
42 дм = 40 дм + 2 дм = 4 м 2 дм
Помни о соотношении числовых значений единиц измерения длины:
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм = 100 см
Рассмотрим выражения.
125 см = 100 см + 20 см + 5 см = 1 м 2 дм 5 см, так как 100 см = 1 м и 20 см = 2дм;
540 см = 500 см + 40 см = 5 м 4 дм, так как 500 см = 5 м и 40 см = 4 дм; 86 мм = 80 мм + 6 мм = 8 см 6 мм, так как 80 мм = 8 см; 42 дм = 40 дм + 2 дм = 4 м 2 дм, так как 40 дм = 4 м.Оформляем задание в тетрадь.
125 см = 1 м 2 дм 5 см
540 см = 5 м 4 дм
86 мм = 8 см 6 мм
42 дм = 4 м 2 дм
Номер 6.
Составь по таблице задачу и реши ее.

В столовой за 6 дней израсходовали 72 кг картофеля, в последующие дни израсходовали 60 кг картофеля. За сколько дней израсходовали 60 кг картофеля, если расходовали в день одинаковое количество картофеля? 1) 72 : 6 = 12 (кг) – расходовали в 1 день. 2) 60 : 12 = 5 (д.) – за столько дней израсходовали 60 кг картофеля. Ответ: 60 кг картофеля израсходовали за 5 дней.
Данная задача: вида «расход в день, количество дней, общий расход» характеризуется зависимостями между элементами:
Расход на день · количество дней = общий расход.
Общий расход : расход в день = количество дней.
Общий расход : количество дней = расход в день.
Составляем задачу.
В столовой за 6 дней израсходовали 72 кг картофеля, в последующие дни израсходовали 60 кг картофеля. За сколько дней израсходовали 60 кг картофеля, если расходовали в день одинаковое количество картофеля?
Рассуждаем.
Каждый день расходуется одинаковое количество картофеля.
Чтобы узнать, расход в день, нужно общий расход разделить на количество дней.
72 : 6 = (60 + 12) : 6 = 10 + 2 = 12 (кг) – картофеля расходовали в 1 день.
Продолжаем рассуждение.
Каждый день расходуется 12 кг картофеля. Чтобы узнать, на сколько дней хватит 60 кг картофеля, нужно общее количество картофеля разделить на расход в день.
60 : 12 = 5 (д.) – за столько дней израсходовали 60 кг картофеля.
Записываем ответ.
Ответ: за 5 дней.
Номер 7.
В столовой 5 дней расходовали по 12 кг крупы, а 2 дня – по 9 кг. Сколько крупы израсходовали за все эти дни?
Запиши задачу в таблицу и реши ее.

1) 12 ∙ 5 = 60 (кг) – крупы израсходовали за 5 дней. 2) 9 ∙ 2 = 18 (кг) – крупы израсходовали за 2 дня. 3) 60 + 18 = 78 (кг) - крупы всего Ответ: за все эти дни всего израсходовали 78 кг крупы.
Данная задача: вида «расход в день, количество дней, общий расход» характеризуется зависимостями между элементами:
Расход на день · количество дней = общий расход.
Общий расход : расход в день = количество дней.
Общий расход : количество дней = расход в день.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
В столовой 5 дней расходовали по 12 кг крупы, значит одинаковое количество. Чтобы узнать это, нужно расход крупы в день умножить на количество дней.
12 ∙ 5 = (10 + 2) ∙ 5 = 50 + 10 = 60 (кг) – крупы израсходовали за 5 дней.
Продолжаем рассуждение.
В столовой 2 дня расходовали по 9 кг крупы, значит одинаковое количество. Чтобы узнать это, нужно расход крупы в день умножить на количество дней.
9 ∙ 2 = 18 (кг) – крупы израсходовали за 2 дня.
Продолжаем рассуждение.
Общий расход складывается из расхода за 5 дней и расхода за 2 дня. Значит, эти значения нужно сложить.
60 + 18 = 78 (кг) – крупы всего израсходовали.
Записываем ответ.
Ответ: 78 кг крупы израсходовали за все дни.
Номер 8.
Начерти в тетради прямоугольник со сторонами 3 см и 6 см. Раскрась его третью часть и вычисли ее площадь.
Ответ:
Площадь закрашенной части 6 ∙ 3 : 3 = 6 см2.
1) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
2) Доля – одна часть из тех, на которые разделили целое.
3) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Начертим прямоугольник.
Начертим прямоугольник со сторонами 6 см и 3 см.
Найдём часть, которую нужно закрасить.
Одна третья часть, значит прямоугольник разделили на 3 части и взяли одну такую часть.
Разделим прямоугольник по вертикали на 3 части.
.jpg)
Рассуждаем.
Для начала найдём площадь прямоугольника со сторонами 6 см и 3 см, перемножив его длину на ширину.
6 ∙ 3 = 18 (см2) – площадь прямоугольника.
Продолжаем рассуждение.
По условию задачи нужно раскрасить третью часть прямоугольника и вычислить её площадь. Для этого разделим площадь прямоугольника на три части.
18 : 3 = 6 (см2) – площадь закрашенной части.
Записываем ответ.
Ответ: 6 – площадь закрашенной части.
Решение выражением: 6 ∙ 3 : 3 = 6 (см2), где 6 ∙ 3 – площадь прямоугольника.
Номер 9.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
3 2 1
80 − 40 : (5 + 35)
2 1 3
57 − 27 : 3 + 24
1 3 2
60 : 3 + 2 · 6
2 1 3
60 : (3 + 2) · 6
1 2
(49 − 42) : 7
1 2
(54 − 24) : 6
Выполняем вычисления по действиям.
3 2 1
80 − 40 : (5 + 35) = 79
1) 5 + 35 = 40
2) 40 : 40 = 1
3) 80 – 79 = 79
2 1 3
57 − 27 : 3 + 24 = 72
1) 27 : 3 = 9
2) 57 – 9 = 48
3) 48 + 24 = 72
1 3 2
60 : 3 + 2 · 6 = 32
1) 60 : 3 = 6 дес. : 3 = 2 дес. = 20
2) 2 ∙ 6 = 12
3) 20 + 12 = 32
2 1 3
60 : (3 + 2) · 6 = 72
1) 3 + 2 = 5
2) 60 : 5 = (50 + 10) : 5 = 10 + 2 = 12
3) 12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72
1 2
(49 − 42) : 7 = 1
1) 49 – 42 = 7
2) 7 : 7 = 1
1 2
(54 − 24) : 6 = 5
1) 54 – 24 = 30
2) 30 : 6 = 5
Оформляем задание в тетрадь.
3 2 1
80 − 40 : (5 + 35) = 80 − 40 : 40 = 80 − 1 = 79
2 1 3
57 − 27 : 3 + 24 = 57 − 9 + 24 = 48 + 24 = 72
1 3 2
60 : 3 + 2 · 6 = 20 + 12 = 32
2 1 3
60 : (3 + 2) · 6 = 60 + 5 · 6 = 12 · 6 = 72
1 2
(49 − 42) : 7 = 7 : 7 = 1
1 2
(54 − 24) : 6 = 30 : 6 = 5
Номер 10.
Найди частное и остаток и выполни проверку.
Ответ:51 : 7 = 7 (ост. 2) Проверка: 1) 2 < 7 2) 7 · 7 + 2 = 51 59 : 9 = 6 (ост. 5) Проверка: 1) 5 < 9 2) 9 · 6 + 5 = 59 78 : 11 = 7 (ост. 1) Проверка: 1) 1 < 11 2) 11 · 7 + 1 = 78 60 : 25 = 2 (ост. 10) Проверка: 1) 10 < 25 2) 25 · 2 + 10 = 60 37 : 10 = 3 (ост. 7) Проверка: 1) 7 < 10 2) 10 · 3 + 7 = 37
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Вычисляем.
51 : 7 = ?
51 не делится на 7 без остатка. Вспомним, какое самое большое число до 51 делится на 7 без остатка. Это 49.
Найдём частное: 49 : 7 = 7.
Найдём остаток: 51 – 49 = 2.
Значит, 51 : 7 = 7 (ост. 2)
59 : 9 = ?
59 не делится на 9 без остатка. Вспомним, какое самое большое число до 59 делится на 9 без остатка. Это 54.
Найдём частное: 54 : 9 = 6.
Найдём остаток: 59 – 54 = 5.
Значит, 59 : 9 = 6 (ост. 5)
78 : 11 = ?
Пробуем в частном 7.
Проверим: 11 ∙ 7 = 77.
Найдем остаток и сравним его с делителем:
78 – 77 = 11, 1 < 11, значит частное 7, а остаток 1.
Значит, 78 : 11 = 7 (ост. 1)
60 : 25 = ?
Пробуем в частном 2.
Проверим: 25 ∙ 2 = 50.
Найдём остаток и сравним его с делителем:
60 – 50 = 10, 10 < 25, значит частное 2, а остаток 10.
Значит, 60 : 25 = 2 (ост. 10)
37 : 10 = ?
37 не делится на 10 без остатка. Вспомним, какое самое большое число до 37 делится на 10 без остатка. Это 30.
Найдём частное: 30 : 10 = 3 дес. : 1дес. = 3
Найдём остаток: 37 – 30 = 7.
Значит, 37 : 10 = 3 (ост. 7)
Сделаем проверку.
Чтобы сделать проверку нужно:
1) убедиться, что остаток меньше делителя;
2) частное умножить на делитель и прибавить к произведению остаток, должно получиться делимое.
Если хотя бы один пункт не выполняется, то деление выполнено не верно.
51 : 7 = 7 (ост. 2)
Проверка:
1) 2 < 7
2) 7 ∙ 7 + 2 = 51
59 : 9 = 6 (ост. 5)
Проверка:
1) 5 < 9
2) 9 ∙ 6 + 5 = 59
78 : 11 = 7 (ост. 1)
Проверка:
1) 1 < 11
2) 11 ∙ 7 + 1 = 78
60 : 25 = 2 (ост. 10)
Проверка:
1) 10 < 25
2) 25 ∙ 2 + 10 = 60
37 : 10 = 3 (ост. 7)
Проверка:
1) 7 < 10
2) 10 ∙ 3 + 7 = 37
Оформляем задание в тетрадь.
51 : 7 = 7 (ост. 2)
Проверка:
2 < 7
7 ∙ 7 + 2 = 51
59 : 9 = 6 (ост. 5)
Проверка:
5 < 9
6 ∙ 9 + 5 = 59
78 : 11 = 7 (ост. 1)
Проверка:
1 < 11
7 ∙ 11 + 1 = 78
60 : 25 = 2 (ост. 10)
Проверка:
10 < 25
2 ∙ 25 + 10 = 60
37 : 10 = 3 (ост. 7)
Проверка:
7 < 10
3 ∙ 10 + 7 = 37
Номер 11.
Используя пары числовых выражений, составь верные равенства:
60 : 4; 48 : 3; 90 : 6; 84 : 7; 36 : 3.
Ответ:60 : 4 = 90 : 6 84 : 7 = 36 : 3
1) Прежде, чем составлять верные равенства, вычисли значение каждого выражения.
2) Равенства – выражения, составленные из чисел, знаков арифметических действий, скобок и знака равно.
Вычислим значения выражений.
Чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
\
60 : 4 = (40 + 20) : 4 = 10 + 5 = 15
48 : 3 = (30 + 18) : 3 = 10 + 6 = 16
90 : 6 = (60 + 30) : 6 = 10 + 5 = 15
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
36 : 3 = (30 + 6) : 3 = 10 + 2 = 12
Составим равенства.
60 : 4 = 90 : 6
15 = 15
84 : 7 = 36 : 3
12 = 12
Номер 12.
Начерти в тетради две такие фигуры. Проведи в каждой из них два отрезка так, чтобы на чертеже, кроме данной фигуры, стало: 1) 2 треугольника, 1 прямоугольник и 2 пятиугольника; 2) 2 треугольника и 6 четырехугольников.


1) Вспомни, какие бывают многоугольники.
2) Вспомни, как обозначать геометрические фигуры буквами.
Начертим.
Начертим фигуру, обозначим её буквами и проведем два отрезка.
-(2024).jpg)
Рассмотрим фигуру.
Получилось:
2 треугольника: ABC и FDE.
1 прямоугольник: ACDF.
2 пятиугольника: ABCDF и ACDEF.
Начертим.
Начертим фигуру, обозначим её буквами и проведем два отрезка.
-(2024).jpg)
Рассмотрим фигуру.
Получилось:
2 треугольника: AOF и OCD.
6 четырехугольников: ABCO, FODE, ABCD, FABC, FCDE, ADEF.
Задание внизу страницы
Запиши и прочитай числа:
Ответ:9 сот. 7 дес. 0 ед. = 970 (девятьсот семьдесят) 8 сот. 0 дес. 0 ед. = 800 (восемьсот)
Вспомни, как образуются и называются трёхзначные числа.
Рассуждаем.
9 сот. 7 дес. 0 ед. = 9 ∙ 1 сот. + 7 ∙ 1 дес. + 0 ед. = 9 ∙ 100 + 7 ∙ 10 + 0 = 900 + 70 + 0 = 970 — девятьсот семьдесят.
8 сот. 0 дес. 0 ед.= 8 ∙ 1 сот. + 0 ∙ 1 дес. + 0 ед. = 8 ∙ 100 + 0 ∙ 10 + 0 = 800 + 0 + 0 = 800 — восемьсот.
Оформляем задание в тетрадь.
.jpg)
Задание на полях страницы
Найди лишнее выражение:
7 · 9 6 · 7 8 · 6 7 · 7 4 · 7 7 · 5 7 · 10
Ответ:8 ∙ 6, так как значение этого выражения не делится на 7.
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Рассмотрим выражения.
7 ∙ 9
6 ∙ 7
8 ∙ 6
7 ∙ 7
4 ∙ 7
7 ∙ 5
7 ∙ 10
Во всех выражения есть множитель 7, кроме выражения 8 ∙ 6
Делаем вывод.
Выражение 8 ∙ 6 – лишнее, так как в нём нет множителя 7.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.