Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 104

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 3.
Ответ:
1) Вспомни названия компонентов при вычитании, и зависимость между компонентами и результатом действия вычитания;
2) Вспомни названия компонентов действия сложения и зависимости между компонентами и результатом действия сложения;
Рассуждаем.
16 – 9 = ?
Чтобы найти разность нужно из уменьшаемого вычесть вычитаемое.
16 – 9 = 16 – (6 + 3) = (16 – 6) – 3 = 10 – 3 = 7
Разность равна 7.
? – 7 = 12
Чтобы найти уменьшаемое нужно к разности прибавить вычитаемое.
12 + 7 = 19
Уменьшаемое равно 19.
30 – ? = 25
Чтобы найти вычитаемое нужно из уменьшаемого вычесть разность.
30 – 25 = 5
Вычитаемое равно 5.
Оформляем задание в тетрадь.
.jpg)
Рассуждаем. 12 + 23 = ?
Чтобы найти сумму нужно слагаемые сложить.
12 + 23 = (10 + 20) + (2 + 3) = 30 + 5 = 35
16 + ? = 50
Чтобы найти одно из слагаемых нужно из суммы вычесть другое слагаемое.
50 – 16 = 34
Слагаемое равно 34.
? + 8 = 90
Чтобы найти одно из слагаемых нужно из суммы вычесть другое слагаемое.
90 – 8 = 82
Слагаемое равно 82.
Оформляем задание в тетрадь.
.jpg)
Номер 4.
Закончи каждый вывод и приведи примеры: Если из суммы вычесть одно из слагаемых, то ... . Если к разности прибавить вычитаемое, то ... . Если из уменьшаемого вычесть разность, то ... .
Ответ:...получится другое слагаемое.
55 + 10 = 65 65 – 10 = 55 65 – 55 = 10
...получится уменьшаемое.
40 – 10 = 30 30 + 10 = 40
...получится вычитаемое.
90 – 15 = 75 90 – 75 = 15
1) Вспомни названия компонентов при вычитании, и зависимость между компонентами и результатом действия вычитания;
2) Вспомни названия компонентов действия сложения и зависимости между компонентами и результатом действия сложения;
Рассмотрим первое высказывание.
Если из суммы вычесть одно из слагаемых, то найдем другое слагаемое.
Рассмотрим пример:
15 + 6 = 21, где
15 и 6 – слагаемые
21 – сумма.
Чтобы найти первое слагаемое нужно из суммы вычесть второе слагаемое.
21 – 6 = 15 – нашли 1 слагаемое.
Чтобы найти второе слагаемое нужно из суммы вычесть первое слагаемое.
21 – 15 = 6 – нашли 2 слагаемое.
Рассмотрим второе высказывание.
Если к разности прибавить вычитаемое, то найдем уменьшаемое.
Рассмотрим пример:
25 – 5 = 20, где
25 – уменьшаемое,
5 – вычитаемое,
20 – разность.
Чтобы найти уменьшаемое нужно к разности прибавить вычитаемое.
20 + 5 = 25 – нашли уменьшаемое.
Рассмотрим третье высказывание.
Если из уменьшаемого вычесть разность, то найдем вычитаемое.
Рассмотрим пример:
70 – 28 = 42, где
70 – уменьшаемое,
28 – вычитаемое,
42 – разность.
Чтобы найти вычитаемое нужно из уменьшаемого вычесть разность. 70 – 42 = (60 + 10) – 42 = (60 – 40) + (10 – 2) = 20 + 8 = 28 – нашли вычитаемое.
Оформим задание в тетрадь.
Если из суммы вычесть одно из слагаемых, то найдем другое слагаемое:
Пример:
15 + 6 = 21,
21 – 6 = 15 – нашли 1 слагаемое
21 – 15 = 6 – нашли 2 слагаемое
Если к разности прибавить вычитаемое, то найдем уменьшаемое:
25 – 5 = 20
20 + 5 = 25 – нашли уменьшаемое.
Если из уменьшаемого вычесть разность, то найдем вычитаемое:
70 – 28 = 42
28 + 42 = 70 – нашли уменьшаемое.
Номер 5.
Объясни, как выполнена проверка сложения и вычитания.
Ответ:
Между разными арифметическими действиями существует связь. Например, чтобы проверить правильно действия умножения, нужно разделить, чтобы проверить вычитание – сложить, чтобы проверить сложение – вычесть. Получается, что сложение проверяют вычитанием. Вычитание проверяют сложением.
1) Вспомни названия компонентов при вычитании, и зависимость между компонентами и результатом действия вычитания;
2) Вспомни названия компонентов действия сложения и зависимости между компонентами и результатом действия сложения;
3) вспомни алгоритм сложения и вычитания в столбик.
Рассуждаем.
Рассмотрим сложение.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
8 + 7 = 15 =
15 ед. – это 1 дес. и 5 ед.
Пишем 5 ед. в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки:4 + 6 + 1 = 11
11 дес. – это 1 сот. и 1 дес.
1 пишем в ответе под десятками, а 1 сот. пойдет в разряд сотен.
Складываем сотни: 3 + 2 + 1 = 6.
6 пишем в ответе в разряде сотен.
Ответ: 615.
Продолжаем рассуждение.
Рассмотрим проверку сложения.
Чтобы выполнить проверку сложения нужно из суммы вычесть одно из слагаемых — получаем другое слагаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 5 отнять 7 нельзя, поэтому занимает 1 единицу у десяток,
1 дес. и 5 ед. – это 16 ед.
16 – 8 = 8.
Пишем 8 в ответ в разряде единиц.
Вычитаем десятки: Было 1 дес., но 1 дес. взяли при вычитании единиц, поэтому осталось 0 дес.
из 0 дес. нельзя отнять 6 дес., поэтому занимаем 1 единицу у сотен:
1 сот. и 0 дес. – это 10 дес.
10 – 6 = 4
4 пишем в ответе под десятками.
Вычитаем сотни: Было 6 сот., но 1 сот. взяли при вычитании десятков, поэтому осталось 5 сот.
5 – 2 = 3
3 пишем в ответ в разделе сотни.
Ответ: 348.
Продолжаем рассуждение.
Рассмотрим вычитание.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 1 отнять 5 нельзя, поэтому занимает 1 единицу у десяток.
1 дес. и 1 ед. – это 11 ед.
11 – 5 = 5.
Пишем 5 в ответ в разряде единиц.
Вычитаем десятки: было 3 дес. заняли 1 дес. и осталось 2 дес.
Из 2 дес. нельзя отнять 7 дес., поэтому занимаем 1 единицу у сотен.
1 сот. и 2 дес. – это 12 дес.
12 – 7 = 5
5 пишем в ответе под десятками.
Вычитаем сотни: Было 4 сот., но 1 сот. взяли при вычитании десяток, поэтому осталось 3 сот.
3 – 1 = 2
2 пишем в ответ в разделе сотни.
Ответ: 256.
Продолжаем рассуждение.
Рассмотрим проверку вычитания.
1 способ. Чтобы выполнить проверку вычитания нужно к разности прибавить вычитаемое — получаем уменьшаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Складываем поочередно, сначала разряд единиц:
6 + 5 = 11 = 1 дес. и 1 ед.
Пишем 1 ед. в ответе под единицами, а 1 дес. пойдет в разряд десяток.
Складываем десятки:
5 + 7 + 1 = 13
13 дес. – это 1 сот. и 3 дес.
Пишем 3 дес. в ответе под десятками, а 1 сот. пойдет в разряд сотен.
Складываем сотни: 2 + 1 + 1 = 4.
4 пишем в ответе в разряде сотен.
Ответ: 431.
Способ 2. Чтобы выполнить проверку вычитания нужно из разности вычесть вычитаемое — получаем уменьшаемое.
.jpg)
Разряд единиц пишем под единицами, десятки под десятками, сотни под сотнями.
Вычитаем поочередно, сначала разряд единиц:
Из 1 отнять 6 нельзя, поэтому занимает 1 единицу у десяток,
1 дес. и 1 ед. – это 11 ед.
11 – 6 = 5.
Пишем 5 в ответ в разряде единиц.
Вычитаем десятки: было 3 дес. заняли 1 дес. и осталось 2 дес.
Из 2 дес. нельзя отнять 5 дес., поэтому занимаем 1 единицу у сотен.
1 сот. и 2 дес. – это 12 сот.
12 – 5 = 7
7 пишем в ответе под десятками.
Вычитаем сотни: Было 4 сот., но 1 сот. взяли при вычитании десяток, поэтому осталось 3 сот.
3 – 2 = 1
1 пишем в ответ в разделе сотни.
Ответ: 175.
Оформляем задание в тетрадь.
.jpg)
Проверка: Если из суммы вычесть одно из слагаемых получится другое слагаемое.
.jpg)
Проверка:
1) Если к разности прибавить вычитаемое, то получится уменьшаемое.
2) Если из уменьшаемого вычесть разность, то получим вычитаемое.
Номер 6.
1) Закончи каждый вывод:
Чтобы найти неизвестное слагаемое, надо ... . Чтобы найти неизвестное уменьшаемое, надо ... . Чтобы найти неизвестное вычитаемое, надо ... .
2) Объясни решение уравнений и проверку.

1) ...из суммы вычесть известное слагаемое. ...к разности прибавить вычитаемое. ...из уменьшаемого вычесть разность.
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Чтобы сделать проверку уравнения нужно вместо неизвестного подставить найденное значение.
Закончим выводы.
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Рассуждаем.
Рассмотрим первое уравнение и его проверку.
38 + х = 72
38 – перовое слагаемое, х – второе слагаемое, 72 – сумма.
Чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое:
х = 72 − 38
.jpg)
х = 34
Проверка: подставим вместо х число 34.
38 + 34 = 72
.jpg)
72 = 72 – уравнение решено верно.
Продолжаем рассуждение.
Рассмотрим второе уравнение и его проверку.
х − 56 = 40
х – уменьшаемое, 56 – вычитаемое, 40 – разность.
Чтобы найти уменьшаемое, надо сложить вычитаемое и разность.
х = 56 + 40
56 + 40 = (50 + 40) + 6 = 90 + 6 = 96
х = 96
Проверка: подставим вместо х число 0.
96 − 56 = (90 − 50) + (6 − 6) = 40
40 = 40 – уравнение решено верно.
Продолжаем рассуждение.
Рассмотрим третье уравнение и его проверку.
90 − х = 42
90 – уменьшаемое, х – вычитаемое, 42 – разность.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
х = 90 − 42
.jpg)
х = 48
Проверка: подставим вместо х число 48.
90 − 48 = 42
.jpg)
42 = 42 – уравнение решено верно.
Оформляем задание в тетрадь.
.jpg)
.jpg)
.jpg)
Номер 7.
Реши с устным объяснением.
Ответ:1) 46 + 3 = 49
37 + 20 = 57
380 + 5 = 385
458 – 50 = 408
100 – 36 = 64
87 + 9 = 96
800 – 200 = 600
960 – 40 = 920
2) 80 + 70 = 150
170 – 80 = 90
390 + 50 = 440
430 – 60 = 370
1) Вспомни как складывать и вычитать по разрядам.
2) Помни, что 1 сот. = 100; 1 дес. = 10.
Рассуждаем.
Рассмотрим первое задание.
1) 46 + 3 = (40 + 6) + 3 = 40 + (6 + 3) = 40 + 9 = 49
Представим число 46 в виде 46 = 40 + 6, сложим число 6 с числом 3, получим 9. Потом к 40 прибавим число 9, получили ответ – 49.
37 + 20 = (30 + 7) + 20 = (30 + 20) + 7 = 50 + 7 = 57
Представим число 37 в виде 37 = 30 + 7, сложим числа 30 и 20, получим 50. Потом к 50 прибавим число 7, получили ответ – 57.
100 – 36 = 100 – (30 + 6) = (100 – 30) – 6 = 70 – 6 = 64
Представим число 36 в виде 36 = 30 + 6, из 100 вычтем 30, получим 70.
Потом из 70 вычтем 6, получим ответ – 64.
87 + 9 = (80 + 7) + 9 = 80 + (7 + 9) = 80 + 16 = 96
Представим число 87 в виде 87 = 80 + 7, сложим число 7 с числом 9, получим 16. Потом к 80 прибавим число 16, получили ответ – 96.
380 + 5 = 3 сот. 8 дес. + 5 ед. = 3 сот. 8 дес. 5 ед. = 385
Представим число 380 в виде разрядов и к нему прибавим 5 единиц, получим 385.
458 – 50 = 4 сот. 5 дес. 8 ед. – 5 дес. = 4 сот. 8 ед. = 408
Представим число 458 в виде разрядов и вычтем из него 5 дес., получим 408.
800 – 200 = 8 сот. – 2 сот. = 6 сот. = 600
Представим числа 800 и 200 в виде разрядов и вычтем 8 сот. из 2 сот., получим 6 сот. = 600.
960 – 40 = (900 + 60) – 40 = 900 + (60 – 40) = 900 + 20 = 920
Представим число 960 в виде 960 = 900 + 60, вычтем из 60 число 40, получим 20. Потом к 900 прибавим число 20, получили ответ – 920.
Продолжаем рассуждение.
Рассмотрим второе задание.
80 + 70 = 8 дес. + 7 дес. = 15 дес. = 150
Представим числа 80 и 70 в виде разрядов и сложим 8 дес. с 7 дес., получим 15 дес. = 150.
390 + 50 = 39 дес. + 5 дес. = 44 дес. = 440
Представим числа 390 и 50 в виде разрядов и сложим 39 дес. с 5 дес., получим 44 дес. = 440.
170 – 80 = 17 дес. – 8 дес. = 9 дес. = 90
Представим числа 170 и 80 в виде разрядов и из 17 дес. вычтем 8 дес.., получим 9 дес. = 90.
430 – 60 = 43 дес. – 6 дес. = 37 дес. = 370
Представим числа 430 и 60 в виде разрядов и из 43 дес. вычтем 6 дес.., получим 37 дес. = 370.
Оформляем задание в тетрадь.
1) 46 + 3 = 40 + (6 + 3) = 40 + 9 = 49
37 + 20 = (30 + 20) + 7 = 50 + 7 = 57
100 – 36 (100 – 30) – 6 = 70 – 6 = 64
87 + 9 = 80 + (7 + 9) = 80 + 16 = 96
380 + 5 = 3 сот. 8 дес. + 5 ед. = 3 сот. 8 дес. 5 ед. = 385
458 – 50 = 4 сот. 5 дес. 8 ед. – 5 дес. = 4 сот. 8 ед. = 408
800 – 200 = 8 сот. – 2 сот. = 6 сот. = 600
960 – 40 = 900 + (60 – 40) = 900 + 20 = 920
2) 80 + 70 = 8 дес. + 7 дес. = 15 дес. = 150
390 + 50 = 39 дес. + 5 дес. = 44 дес. = 440
170 – 80 = 17 дес. – 8 дес. = 9 дес. = 90
430 – 60 = 43 дес. – 6 дес. = 37 дес. = 370
Номер 8.
Реши и выполни проверку.
Ответ:

1) Вспомни алгоритм сложения и вычитания в столбик.
2) Помни, что пишем единицы под единицами, десятки под десятками, а сотни под сотнями.
Выполним вычисления с пояснениями.
Выполним сложение двухзначных чисел.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Складываю единицы: 4 + 6 = 10
10 ед. – это 1 дес. и 0 ед.; 0 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 2 + 3 + 1 = 6
Пишу 6 под десятками.
Читаю ответ: 60.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Складываю единицы: 8 + 7 = 15
15 ед. – это 1 дес. и 5 ед.; 5 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 3 + 4 + 1 = 8
Пишу 8 под десятками.
Читаю ответ: 85.
Выполним вычитание двухзначных чисел.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Вычитаю единицы: из 6 ед. нельзя вычесть 9 ед. Беру 1 ед. из 5 дес. чтобы не забыть ставлю точку над цифрой 5)
1 дес. и 6 ед. – это 16 ед.
16 – 9 = 7
Пишу под единицами 7.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 5 – 2 – 1 = 2
Пишу под десятками 2.
Читаю ответ: 27.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Вычитаю единицы: из 0 ед. нельзя вычесть 4 ед. Беру 1 ед. из 6 дес. чтобы не забыть ставлю точку над цифрой 6)
1 дес. и 0 ед. – это 10 ед.
10 – 4 = 6
Пишу под единицами 6.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 6 – 4 – 1 = 1
Пишу под десятками 1.
Читаю ответ: 16.
Выполним вычитание трехзначных чисел.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: 5 – 3 = 2
Пишу под единицами 2.
Вычитаю десятки: 7 – 2 = 5
Пишу под десятками 5.
Вычитаю сотни: 2 – 1 = 1
Пишу под сотнями 1.
Читаю ответ: 152.
Выполним сложение трёхзначных чисел.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 8 + 9 = 17
17 ед. – это 1 дес. и 7 ед.; 7 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 6 + 0 + 1 = 7
Пишу под десятками 6.
Складываю сотни: 5 + 2 = 7
Пишу под сотнями 7.
Читаю ответ: 777.
Сделаем проверку.
24 + 36 = 60.
Чтобы сделать проверку сложения нужно из суммы вычесть одно из слагаемых.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Вычитаю единицы: из 0 ед. нельзя вычесть 6 ед. Беру 1 ед. из 6 дес. чтобы не забыть ставлю точку над цифрой 6)
1 дес. и 0 ед. – это 10 ед.
10 – 6 = 4
Пишу под единицами 4.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 6 – 3 – 1 = 2
Пишу под десятками 2.
Читаю ответ: 24.
38 + 47 = 85
Чтобы сделать проверку сложения нужно из суммы вычесть одно из слагаемых.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Вычитаю единицы: из 5 ед. нельзя вычесть 7 ед. Беру 1 ед. из 8 дес. чтобы не забыть ставлю точку над цифрой 8)
1 дес. и 5 ед. – это 15 ед.
15 – 7 = 8
Пишу под единицами 8.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 8 – 4 – 1 = 3
Пишу под десятками 3.
Читаю ответ: 38.
56 – 29 = 27
Чтобы выполнить проверку вычитания нужно к разности прибавить вычитаемое.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Складываю единицы: 7 + 9 = 16
16 ед. – это 1 дес. и 6 ед.; 6 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 2 + 2 + 1 = 5
Пишу 5 под десятками.
Читаю ответ: 56.
60 – 44 = 16
Чтобы выполнить проверку вычитания нужно к разности прибавить вычитаемое.
.jpg)
Пишу: единицы под единицами, а десятки под десятками.
Складываю единицы: 4 + 6 = 10
10 ед. – это 1 дес. и 0 ед.; 0 ед. пишу под единицами, а 1 дес. прибавляю к десяткам.
Складываю десятки: 1 + 4 + 1 = 6
Пишу 6 под десятками.
Читаю ответ: 60.
275 – 123 = 152
Чтобы выполнить проверку вычитания нужно к разности прибавить вычитаемое.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Складываю единицы: 2 + 3 = 5
Пишу 5 под единицами.
Складываю десятки: 5 + 2 = 7
Пишу 7 под десятками.
Складываю сотни: 1 + 1 = 2
Пишу 2 под сотнями.
Читаю ответ: 275.
568 + 209 = 777
Чтобы сделать проверку сложения нужно из суммы вычесть одно из слагаемых.
.jpg)
Пишу: единицы под единицами, десятки под десятками, а сотни под сотнями.
Вычитаю единицы: из 7 ед. нельзя вычесть 9 ед. Беру 1 дес. из 7 дес. (Чтобы не забыть об этом, ставлю точку над цифрой 7.)
1 дес. и 7 ед. – это 17 ед.
17 – 9 = 8
Пишу под единицами 8.
Вычитаю десятки: так как занимали 1 ед. у десяток, то 7 – 0 – 1 = 6
Пишу под десятками 6.
Вычитаю сотни: 7 – 2 = 5
Пишу под сотнями 5.
Читаю ответ: 568.
Оформим задание в тетрадь.
.jpg)
Задание на полях страницы
Головоломка:

Треугольник = 32
Квадрат = 17
Круг = 46
Проверка:
46 + 32 = 78
32 - 17 = 15
17 + 13 = 30
Вместо фигур нужно вставить числа, чтобы равенства стали верными.
Рассуждаем.
Рассмотрим последнее выражение.
+ 13 = 30
Неизвестно слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
30 – 13 = 17
Значит, число за розовым квадратом – это число 17.
Продолжаем рассуждение.
Рассмотрим второе выражение.
Во 2 примере заменим квадрат на число 17, получим:
– 17 = 15
Неизвестно уменьшаемое.
Чтобы найти уменьшаемое нужно к разности прибавить вычитаемое.
15 + 17 = 32
Значит, число за синим треугольником – это число 32.
Продолжаем рассуждение.
Рассмотрим первое выражение.
В 1 примере заменим треугольник на число 32, получим:
+ 32 = 78
Неизвестно слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
78 – 32 = 56
Значит, число за зеленым кругом – это число 56.
Делаем проверку.
56 + 32 = (50 + 30) + (6 + 2) = 70 + 8 = 78
32 – 17 = 32 – (12 + 5) = (32 – 12) – 5 = 20 – 5 = 15
17 + 13 = (10 + 10) + (7 + 3) = 20 + 10 = 30
Оформляем задание в тетрадь.
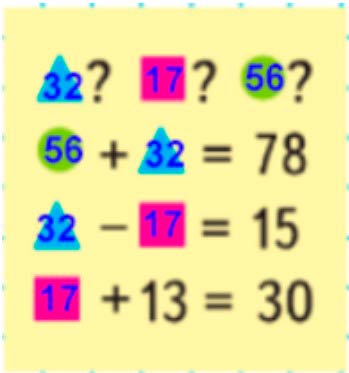
Ответ:
Треугольник = 32
Квадрат = 17
Круг = 56
Умножение и деление
Номер 1.
Объясни, почему верны равенства.
Ответ:Равенства верны, потому что верны их левые и правые части.
Используются следующие свойства:
1) а ∙ b = b ∙ a – переместительное свойство умножения;
2) (а + b) ∙ c = а ∙ с + b ∙ c – умножение суммы на число;
3) (а + b) : c = а : с + b : c – деление суммы на число;
4) а ∙ 0 = 0; а ∙ 1 = а; 0 : а = 0 – умножение числа на 0 и 1, деление 0 на число.
Рассуждаем и выполняем вычисления.
Рассмотрим первое равенство:
7 ∙ 14 = 14 ∙ 7 – если множители поменять местами, произведение не изменится.
Проверка:
7 ∙ 14 = 7 ∙ (10 + 4) = 70 + 28 = 98
14 ∙ 7 = (10 + 4) ∙ 7 = 70 + 28 = 98
98 = 98
(6 + 7) ∙ 5 = 6 ∙ 5 + 7 ∙ 5 – чтобы умножить сумму на число, можно сначала сложить числа, а потом умножить на число, или поочередно умножить каждое слагаемое на число, а потом сложить.
Проверка:
(6 + 7) ∙ 5 = 13 ∙ 5 = 50 + 15 = 65
6 ∙ 5 + 7 ∙ 5 = 30 + 35 = 65
65 = 65
(18 + 24) : 6 = 18 : 6 + 24 : 6 – чтобы разделить сумму на число, можно сначала сложить числа, а потом разделить на число, или поочередно разделить каждое слагаемое на число, а потом сложить.
Проверка:
(18 + 24) : 6 = 42 : 6 = 7
18 : 6 + 24 : 6 = 3 + 4 = 7
7 = 7
28 ∙ 1 = 28 – если число умножить на 1, то значение не изменится.
Проверка:
28 ∙ 1 = 28
28 = 28
49 ∙ 0 = 0 – если число умножить на 0, то получится 0.
Проверка:
49 ∙ 0 = 0
0 = 0
0 : 17 = 0 – если делимое равно 0, то частное тоже равно 0.
Проверка:
0 : 17 = 0
0 = 0
Делаем вывод.
Равенства равны, так как справа и слева одинаковые значения.
Номер 2.
Ответ:
1) Вспомни названия компонентов при умножении, и зависимость между компонентами и результатом действия умножения;
2) Вспомни названия компонентов при делении и зависимости между компонентами и результатом действия деления.
Рассуждаем.
Таблица 1.
8 ∙ 7 = ?
Чтобы найти произведение, нужно множители умножить.
8 ∙ 7 = 56
? ∙ 9 = 72
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
72 : 9 = 8
6 ∙ ? = 42
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
42 : 6 = 7
Продолжаем рассуждения.
Таблица 2.
54 : 9 = ?
Чтобы найти частное, нужно делимое разделить на делитель.
54 : 9 = 6
? : 8 = 6
Чтобы найти делимое, нужно частное умножить на делитель.
6 ∙ 8 = 48
63 : ? = 7
Чтобы найти делитель, нужно делимое разделить на частное.
63 : 7 = 9
Оформляем задание в тетрадь.
.jpg)
Номер 3.
Закончи каждый вывод и приведи примеры:
Если произведение разделить на один из множителей, то получится ... . Если делитель умножить на частное, то получится ... . Если делимое разделить на частное, то получится ... .
Ответ:Если произведение разделить на один из множителей, то получится другой множитель.
23 ∙ 2 = 46
Разделим 46 на 2, получится 23.
Если делитель умножить на частное, то получится делимое.
27 : 3 = 9
Умножим 3 на 9, получится 27.
Если делимое разделить на частное, то получится делитель.
45 : 5 = 9
Разделим 45 на 9, получится 5.
1) Вспомни названия компонентов при умножении, и зависимость между компонентами и результатом действия умножения;
2) Вспомни названия компонентов при делении и зависимости между компонентами и результатом действия деления.
Рассмотрим первое высказывание.
Если произведение разделить на один из множителей, то получится другой множитель.
Рассмотрим пример: 23 ∙ 2 = 46,
23 – первый множитель, 2 – второй множитель, 46 – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
46 : 2 = 23 – нашли первый множитель.
Рассмотрим второе высказывание.
Если делитель умножить на частное, то получится делимое.
Рассмотрим пример: 27 : 3 = 9,
27 – делимое, 3 – делитель, 9 – частное.
Чтобы найти делимое, нужно делитель умножить на частное.
3 ∙ 9 = 27 – нашли делимое.
Рассмотрим третье высказывание.
Если делимое разделить на частное, то получится делитель.
Рассмотрим пример: 45 : 5 = 9,
45 – делимое, 5 – делитель, 9 – частное.
Чтобы найти делитель, нужно делимое разделить на частное.
45 : 9 = 5 – нашли делитель.
Оформим задание в тетрадь.
Если произведение разделить на один из множителей, то получится другой множитель.
Пример: 23 ∙ 2 = 46,
46 : 2 = 23 – нашли множитель.
Если делитель умножить на частное, то получится делимое.
Пример: 27 : 3 = 9,
3 ∙ 9 = 27 – нашли делимое.
Если делимое разделить на частное, то получится делитель.
Пример: 45 : 5 = 9
45 : 9 = 5 – нашли делитель.
Номер 4.
Объясни, как выполнена проверка умножения и деления.
Ответ:Первая пара выражений: если произведение разделить на первый множитель, то получится другой множитель.
Вторая пара выражаней: если частное умножить на делитель, то получится делимое.
75 : 5 = 15;
15 ∙ 5 = 75.
1) Вспомни названия компонентов при умножении, и зависимость между компонентами и результатом действия умножения;
2) Вспомни названия компонентов при делении и зависимости между компонентами и результатом действия деления.
Рассуждаем.
Рассмотрим умножение.
32 ∙ 3 = (30 + 2) ∙ 3 = 90 + 6 = 96
32 – множитель, 3 – множитель, 96 – произведение.
Продолжаем рассуждения.
Рассмотрим проверку умножения.
Чтобы проверить умножение, нужно произведение разделить на один из множителей – получаем другой множитель.
1) 96 : 32 = ?
Пробуем в частном 2 и проверяем:
32 ∙ 2 = 64, 64 < 96, число 2 не подходит.
Пробуем в частном 3 и проверяем:
32 ∙ 3 = 96, 96 = 96, значит:
96 : 32 = 3.
2) 96 : 3 = (90 + 6) : 3 = 30 + 2 = 32
Продолжаем рассуждения.
Рассмотрим деление.
75 : 5 = (50 + 25) : 5 = 10 + 5 = 15
75 – делимое, 5 – делитель, 15 – частное.
Продолжаем рассуждения.
Рассмотрим проверку деления.
1) Чтобы проверить деление, можно умножить частное на делитель – получим делимое.
15 ∙ 5 = (10 + 5) ∙ 5 = 50 + 25 = 75
2) Чтобы проверить деление, можно разделить делимое на частное – получим делитель.
75 : 15 = 5
Пробуем в частном 4 и проверяем:
15 ∙ 4 = 60, 60 < 75, число 4 не подходит.
Пробуем в частном 5 и проверяем:
15 ∙ 5 = 75, 75 = 75, значит,
75 : 15 = 5.
Оформляем задание в тетрадь.
1) 32 ∙ 3 = 96
Чтобы проверить умножение, нужно произведение разделить на один из множителей – получаем другой множитель.
96 : 32 = 3 или 96 : 3 = 32
2) 75 : 5 = 15
Чтобы проверить деление, можно умножить частное на делитель – получим делимое.
15 ∙ 5 = 75
Чтобы проверить деление, можно разделить делимое на частное – получим делитель.
75 : 15 = 5
Номер 5.
1) Закончи каждый вывод:
Чтобы найти неизвестный множитель, надо ... . Чтобы найти неизвестное делимое, надо ... . Чтобы найти неизвестный делитель, надо ... .
2) Объясни решение уравнений и проверку.
3) Реши уравнения, не вычисляя.

1) Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
2) В первом уравнении нужно найти неизвестный множитель. Решаем делением, а проверяем
умножением.
Во втором уравнении нужно найти делимое. Решаем умножением, а проверяем делением.
В третьем уравнении нужно найти делитель. Решаем и проверяем делением.
3) х ∙ 18 = 18
х = 1
х ∙ 24 = 0
х = 0
36 : х = 1
х = 36
х : 1 = 17
х = 17
1) Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Чтобы сделать проверку уравнения, нужно вместо неизвестного подставить найденное значение.
Закончим выводы.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Чтобы найти неизвестное делимое, надо частное умножить на делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Рассуждаем.
Рассмотрим первое уравнение и его проверку.
х ∙ 24 = 72
х – первый множитель, 24 – второй множитель, 72 – произведение.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель,
х = 72 : 24
х = 3.
Проверка: подставим вместо х число 3.
3 ∙ 24 = 3 ∙ (20 + 4) = 60 + 12 = 72.
72 = 72 – уравнение решено верно.
Продолжаем рассуждения.
Рассмотрим второе уравнение и его проверку.
х : 18 = 5
х – делимое, 18 – делитель, 5 – частное.
Чтобы найти делимое, нужно делитель умножить на частное.
х = 18 ∙ 5
х = 90.
Проверка: подставим вместо х число 90.
90 : 18 = 5.
5 = 5 – уравнение решено верно.
Продолжаем рассуждения.
Рассмотрим третье уравнение и его проверку.
51 : х = 17
51 – делимое, х – делитель, 17 – частное.
Чтобы найти делитель нужно делимое разделить на частное.
51 : х = 17
х = 3.
Проверка: подставим вместо х число 3.
51 : 3 = 17.
17 = 17 – уравнение решено верно.
Продолжаем рассуждения.
Выполним вычисления.
х ∙ 18 = 18 – если число умножить на 1, то значение не изменится.
х = 1
х ∙ 24 = 0 – если число умножить на 0, то произведение равно 0.
х = 0
36 : х = 1 – если число разделить на само себя, то получится 1.
х = 36
х : 1 = 17 – если число разделить на 1, то значение не изменится.
х = 17
Оформляем задание в тетрадь.
1) Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
2) В 1 уравнении нужно найти неизвестный множитель. Решается делением, а проверяется умножением.
Во 2 уравнении нужно найти делимое. Решается умножением, а проверяется делением.
Во 3 уравнении нужно найти делитель. Решается и проверяется делением.
3)
х ∙ 18 = 18
х = 1
х ∙ 24 = 0
х = 0
36 : х = 1
х = 36
х : 1 = 17
х = 17
Задание на полях страницы
Головоломка:

Треугольник = 8
Квадрат = 3
Круг = 7
Проверка:
7 * 8 = 56
8 * 3 = 24
3 * 7 = 21
Вместо фигур нужно вставить числа, чтобы равенства стали верными.
Рассуждаем.
Рассмотрим последнее выражение.
□ ∙ 7 = 21
Неизвестен множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
21 : 7 = 3
Значит, число за розовым квадратом – это число 3.
Продолжаем рассуждение.
Рассмотрим второе выражение.
Во 2 примере заменим квадрат на число 3, получим:
∆ ∙ 3 = 24
Неизвестен множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
24 : 3 = 8
Значит, число за синим треугольником – это число 8.
Продолжаем рассуждение.
Рассмотрим первое выражение.
В 1 примере заменим треугольник числом 8, получим:
◯ ∙ 8 = 56
Неизвестен множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
56 : 8 = 7
Значит, число за зеленым кругом – это число 8.
Делаем проверку.
7 ∙ 8 = 56
8 ∙ 3 = 24
3 ∙ 7 = 21
Оформляем задание в тетрадь.
Треугольник – 8
Квадрат – 3
Круг – 7
Проверка:
7 ∙ 8 = 56
8 ∙ 3 = 24
3 ∙ 7 = 21
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.