Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 93

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 93

Номер 3.

Масса одного ящика с мандаринами 8 кг. Найди массу 9 коробок с бананами, если одна коробка с бананами на 3 кг легче одного ящика с мандаринами.

Ответ:

математика 3 класс Моро, Бантова - 1 часть страница 93, номер 3

1-й способ решения: 1) 8 – 3 = 5 (кг) – масса ящика с бананами. 2) 5 · 9 = 45 (кг) – общая масса Ответ: 45 кг масса 9 коробок с бананами.
2-й способ решения: (8 – 3) · 9 = 5 · 9 = 45 (кг) – масса 9 коробок с бананами Ответ: 45 кг.

Подсказка:

Данная задача: вида «масса 1 ящика, количество ящиков, общее кол-во мандаринов» характеризуется зависимостями между компонентами:

Масса 1 ящика · кол-во ящиков = общее кол-во мандаринов.
Общее кол-во мандаринное : масса 1 ящика = кол-во ящиков.
Общее кол-во мандаринов : кол-во ящиков = масса 1 ящика.

Шаг 1.
Оформляем условие в виде краткой записи или таблицы.

Краткая запись:

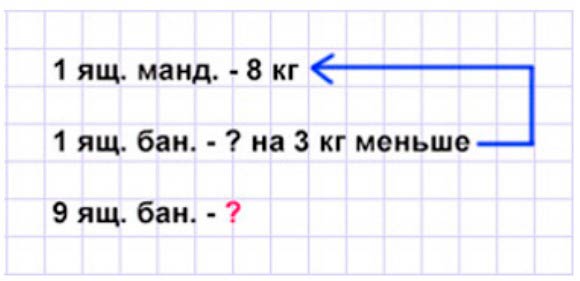
Таблица:

Шаг 2.
Рассуждаем.

Масса одного ящика с мандаринами – 8 кг, а масса одной коробки с бананами на 3 кг легче. Значит, что масса одной коробки такая же, как масса ящика, но без 3 кг. Соответственно, чтобы узнать, какова масса коробки, нужно из массы ящика вычесть 3 кг.

8 − 3 = 5 (кг) – масса 1 ящика с бананами.

Шаг 3.
Продолжаем рассуждение.

Общее количество бананов складывается из количества бананов каждой коробки. Соответственно, чтобы узнать, сколько всего бананов было, нужно сложить количество бананов каждой коробки.
Но количество бананов в каждой коробке одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.

5 ∙ 9 = 45 (кг) − масса 9 коробок с бананами.

Шаг 4.
Записываем ответ.

Ответ: 45 кг масса 9 коробок с бананами.

Решение выражением:
(8 – 3) · 9 = 45 (кг), где 8 – 3 – количество бананов в 1 ящике.

Номер 4.

Реши уравнения, подбирая значения х.

Ответ:

72 : х = 9 х = 72 : 9 х = 8 Проверка: 72 : 8 = 9 9 = 9 Ответ: х = 8
8 · х = 64 х = 64 : 8 х = 8 Проверка: 8 · 8 = 64 64 = 64 Ответ: х = 8
х : 7 = 4 х = 4 * 7 х = 28 Проверка: 28 : 7 = 4 4 = 4 Ответ: х = 28

Подсказка:

Шаг 1.
Рассмотрим уравнения.

72 : х = 9,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.

8 · х = 64,
х - неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.

х : 7 = 4,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.

Шаг 2.
Решим уравнение методом подбора.

72 : х = 9
Вспомни таблицу умножения на 9.
На какое число нужно умножить число 9, чтобы значение было равно 72?
Это число 8.
Значит х = 8.

8 ∙ х = 64
Вспомни таблицу умножения на 8.
На какое число нужно умножить число 8, чтобы получилось 64?
Это число 8.
Значит х = 8.

х : 7 = 4
Вспомни таблицу умножения на 7.
Какое получится число при умножении 7 на 4?
Это число 28.
Значит, х = 28

Шаг 3.
Делаем проверку.

72 : х = 9
Проверка: вместо х подставим число 8.
72 : 8 = 9, так как 8 · 9 = 72
72 = 72 – верно.

8 · х = 64
Проверка: вместо х подставим число 8.
8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
64 = 64 – верно.

х : 7 = 4
Проверка: вместо х подставим число 28.
28 : 7 = 4, так как 7 · 4 = 28
28 = 28 – верно.

Номер 5.

Реши уравнения с устным объяснением.

Ответ:

математика 3 класс Моро, Бантова - 1 часть страница 93, номер 5

Подсказка:

1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.

2) Вспомни зависимость между компонентами и результатом действия умножения и деления.

3) Помни, что при умножении любого числа на 1, получается число, которое умножали.

4) Существует еще и другие: умножение числа на 0, и 0 на любое число.

Шаг 1.
Рассмотрим уравнения.

35 : х = 1,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.

х · 10 = 10,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.

х · 12 = 0,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.

х : 8 = 0,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.

Шаг 2.
Решим уравнение, с объяснением.

35 : х = 1
х = 35 : 1
х = 35
Если число разделить на само себя, то получится 1.

х ∙ 10 = 10
х = 10 : 10
х = 1
Если число умножить на 1, то результат не изменится.

х ∙ 12 = 0
х = 0 : 12
х = 0
Если произведение равно 0, значит хотя бы один из множителей равен 0.

х : 8 = 0
х = 8 ∙ 0
х = 0
Если частное равно 0, значит и делимое равно 0, так как делитель не может быть равен 0.

Шаг 3.
Делаем проверку.

35 : х = 1
Проверка: вместо х подставим число 35.
35 : 35 = 1
При делении числа на само себя, получается 1.
1 = 1 – верно.

х ∙ 10 = 10
Проверка: вместо неизвестного подставим число 1.
1 · 10 = 10
Если число умножить на 1, то число не изменится.
10 = 10 – верно.

х ∙ 12 = 0
Проверка: вместо х подставим число 0.
0 · 12 = 0
Если число умножить на нуль, то получим нуль.
0 = 0 – верно.

х : 8 = 0
Проверка: вместо х подставим число 0.
0 : 8 = 0
Если нуль разделить на любое число, то получим нуль.
0 = 0 – верно.

Номер 6.

Найди значение выражения.

Ответ:

1) а : 7 если а = 49, то 49 : 7 = 7 если а = 35, то 35 : 7 = 5 если а = 56, то 56 : 7 = 8 если а = 63, то 63 : 7 = 9
2) b ∙ 8 если b = 9, то 9 ∙ 8 = 72 если b = 8, то 8 ∙ 8 = 64 если b = 7, то 7 ∙ 8 = 56

Подсказка:

1) а : 7, значит, уменьшить число а в 7 раз, т.е. разделить на 7.

2) b · 8, значит, увеличить число b в 8 раз, т.е. умножить на 8.

Задание 1.

Шаг 1.
Рассуждаем.

а : 7

49 : 7 = 7, так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

35 : 7 = 5, так как 7 · 5 = 35,
где 7 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

56 : 7 = 8, так как 7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

63 : 7 = 9, так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

Шаг 2.
Оформляем задание в тетрадь.

a : 7, если:
a = 49, то 49 : 7 = 7
a = 35, то 35 : 7 = 5
a = 56, то 56 : 7 = 8
a = 63, то 63 : 7 = 9

Задание 2.

Шаг 1.
Рассуждаем.

b · 8

9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

8 · 8 = 64,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

Шаг 2.
Оформляем задание в тетрадь.

b ∙ 8, если:
b = 9, то 9 ∙ 8 = 72
b = 8, то 8 ∙ 8 = 64
b = 7, то 7∙ 8 = 56

Номер 7.

Ответ:

Подсказка:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.

Шаг 1.
Расставляем порядок действий.

2 1
75 − 8 · 4 = 43
В данном выражении присутствуют действия вычитание и умножение. Вначале выполним действие умножение, а потом действие вычитание.

2 1
60 − 7 · 7 = 11
В данном выражении присутствуют действия вычитание и умножение. Вначале выполним действие умножение, а потом действие вычитание.

2 1
84 + 64 : 8 = 92
В данном выражении присутствуют действия сложение и деление. Вначале выполним действие деление, а потом действие сложение.

2 1
36 + 56 : 8 = 43
В данном выражении присутствуют действия сложение и деление. Вначале выполним действие деление, а потом действие сложение.

1 3 2
3 · 9 + 4 · 3 = 39
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а потом действие сложение.

1 3 2
5 · 7 + 6 · 8 = 83
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а потом действие сложение.

Шаг 2.
Выполняем вычисления по действиям.

2 1
75 − 8 · 4 = 43
1) 8 · 4 = 32,
где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

2) 75 − 32 = (70 – 30) + (5 – 2) = 40 + 3 = 43

Выполняем вычитание по разрядам – из десяток вычитаем десятки, а из единиц – единицы.

2 1
60 − 7 · 7 = 11
1) 7 ∙ 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
2) 60 − 49 = 11

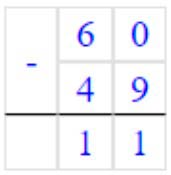
Вычитаем единицы. От числа 0 мы не можем отнять 9.
Занимаем 1 дес. = 10 ед., 10 – 9 = 1 – получилось единиц.
Записываем в разряде единиц число 1.
Вычитаем десятки. Было 6 дес., мы занимали 1 дес, осталось 6 – 1 = 5 дес.,
5 – 4 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 11.

2 1
84 + 64 : 8 = 92
1) 64 : 8 = 8,так как 8 · 8 = 64
2) 84 + 8 = 92

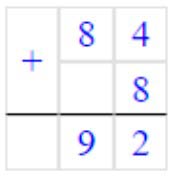
Складываем единицы. 4 + 8 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. Было 8 дес. и ещё 1 дес., который запомнили 8 + 1 = 9 – получилось десяток.
Записываем в разряде десятков число 9.
Читаем ответ: 92.

2 1
36 + 56 : 8 = 43
1) 56 : 8 = 7,так как 8 · 7 = 56
2) 36 + 7 = 43

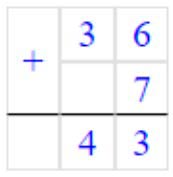
Складываем единицы. 6 + 7 = 13 – получилось 1 дес. и 3 ед.
Записываем в разряде единиц число 3, а 1 дес. запоминаем.
Складываем десятки. Было 3 дес. и ещё 1 дес., который запомнили 3 + 1 = 4 – получилось десяток.
Записываем в разряде десятков число 4.
Читаем ответ: 43.

1 3 2
3 · 9 + 4 · 3 = 39
1) 3 ∙ 9 = 27,
где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

2) 4 ∙ 3 = 12,
где 4 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.

3) 27 + 12 = (20 + 10) + (7 + 2) = 30 + 9 = 39

Выполняем сложение по разрядам – десятки складываем с десятками, а единицы – с единицами.

1 3 2
5 · 7 + 6 · 8 = 83
1) 5 ∙ 7 = 35,
где 5 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
2) 6 ∙ 8 = 48
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
3) 35 + 48 = 83

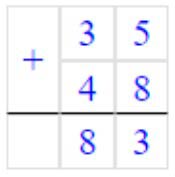
Складываем единицы. 5 + 8 = 13 – получилось 1 дес. и 3 ед.
Записываем в разряде единиц число 3, а 1 дес. запоминаем.
Складываем десятки. 3 + 4 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десяток.
Записываем в разряде десятков число 8.
Читаем ответ: 83.

Шаг 3.
Оформляем задание в тетрадь.

75 – 8 · 4 = 75 – 32 = 43
60 – 7 · 7 = 60 – 49 = 11
84 + 64 : 8 = 84 + 8 = 92
36 + 56 : 8 = 36 + 7 = 43
3 · 9 + 4 · 3 = 27 + 12 = 39
5 · 7 + 6 · 8 = 35 + 48 = 83

Номер 8.

Рассмотри рисунок и определи, кто из девочек какую долю закрасил, если Таня закрасила большую долю, чем Оля, а Лена закрасила большую долю, чем Таня.

Ответ:

Лена закрасила одну третью долю (рис.1). Таня закрасила одну шестую (рис.3). А Оля закрасила одну двенадцатую (рис. 2).

Подсказка:

1) Доля – одна часть из тех, на которые разделили целое.

2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.

Шаг 1.
Рассмотрим доли на каждом рисунке.

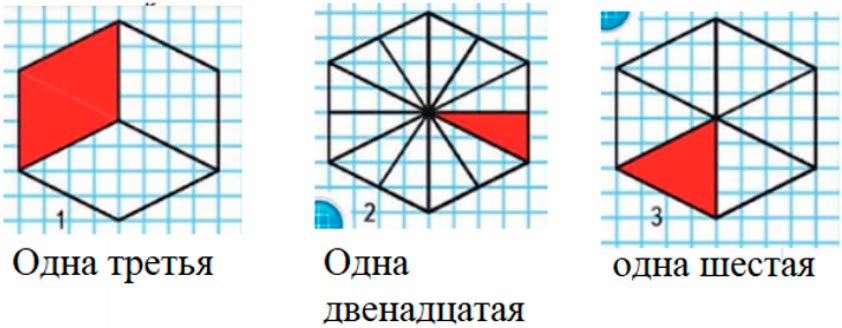
Рисунок 1. Фигура разделена на три равные части и закрашена одна из этих частей, значит закрашена одна третья часть.

Рисунок 2. Фигура разделена на двенадцать равных частей и закрашена одна из этих частей, значит закрашена одна двенадцатая часть.

Рисунок 3. Фигура разделена на шесть равных частей и закрашена одна из этих частей, начит закрашена одна шестая часть.

Шаг 2.
Продолаем рассудение.

Одну и туже фигуру делили на разное количество частей. Чем на большее количесвто частей разделён прямоугольник, тем меньше сама будет одна эта часть или та доля больше, где число меньше.

Расположим доли в порядке возрастания, то есть от меньшей доли к большей доли: одна двенадцатая → одна шестая → одна третья.

Шаг 3.
Делаем вывод.

Вспомним условия задачи:

Лена закрасила больше Тани, а Таня закрасила больше чем Оля, значит:
Таня > Оля и Лена > Таня.

Расположим девочек в порядке возрастания, закрашенной части, то есть от меньшей к большей:
Оля → Таня → Лена.

Тогда Лена закрасила одну третью часть, Таня – одну шестую часть, Оля – одну двенадцатую часть.

Шаг 4.
Записываем ответ.

Ответ: Лена закрасила фигуру 1, Таня – фигуру 3, Оля – фигуру 2.

Номер 9.

Начерти квадрат со стороной 4 см. Раздели его на 2 равных прямоугольника и закрась один из них красным цветом. Другой прямоугольник раздели на 2 равных квадрата и закрась один из них синим цветом. Другой квадрат раздели на 2 равных треугольника и закрась один из них зеленым цветом. Какая доля большого квадрата осталась незакрашенной?

Ответ:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 93, номер 9

Осталась не закрашенной одна восьмая доля. Это хорошо видно, если незакрашенный квадрат разделить на одинаковые части.

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 93, номер 9-1

Подсказка:

Шаг 1.
Выполним задание.

1) Начертим квадрат со стороной 4 см.

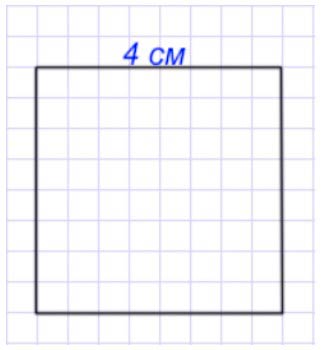
2) Разделим его на 2 равных прямоугольника и закрасим один из них красным цветом.

Красным цветом закрашена одна вторая квадрата.

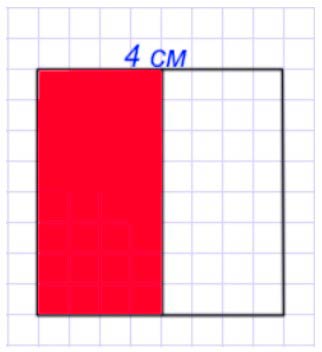
3) Другой прямоугольник разделим на 2 равных квадрата и закрасим один из них синим цветом.

Синим цветом закрашена половина от одной второй части, значит закрашена одна четвертая часть.

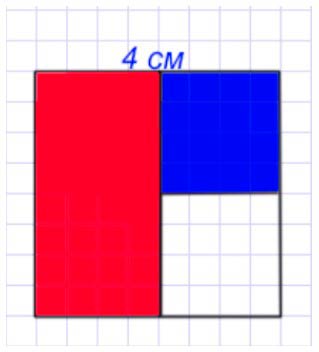
4) Другой квадрат разделим на 2 равных треугольника и закрасим один из них зеленым цветом.

Зеленым цветом закрашена половина от одной четвертой части, значит закрашена одна восьмая часть.

Шаг 2.
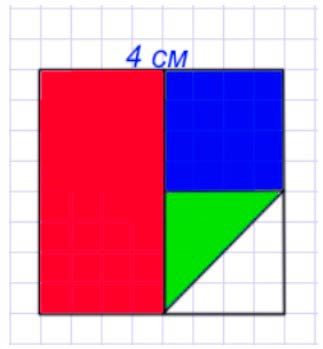
Делаем вывод.

Осталась не закрашенной одна восьмая доля.
Это хорошо видно, если не закрашенный квадрат разделить на одинаковые части, то есть разделить на 8 одинаковых треугольников.

Задание внизу страницы

Начерти квадрат, длина стороны которого 3 см. Раздели его на равные части так, чтобы можно было закрасить одну девятую его часть; одну третью.

Ответ:

Одна девятая часть:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 93, задание внизу страницы

Одна третья часть:

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 93, задание внизу страницы 2

Подсказка:

Шаг 1.
Выполним задание.

Квадрат – геометрическая фигура, четырехугольник, прямоугольник, у которого все стороны равны. Квадрат – это целое.

Одна девятая, значит, доля указывает на то, на сколько частей разделить целое.
Чтобы закрасить одну девятую часть квадрата нужно квадрат разделить на 9 равных частей и закрасить одну из этих частей.

Шаг 2.
Продолжаем выполнение задания.

Одна третья, значит, доля указывает на то, на сколько частей разделить целое.
Чтобы закрасить одну третью часть квадрата нужно квадрат разделить на 3 равные части и закрасить только одну из этих частей.