Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 8

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Закончи вывод.
Если к разности прибавить вычитаемое, получится ... .
Зная это, можно решать уравнения, в которых неизвестным является уменьшаемое.
Если к разности прибавить вычитаемое, получится уменьшаемое.
Вспомни названия элементов при вычитании,
1) Уменьшаемое – это число, из которого вычитают, оно становится меньше, то есть уменьшается.
2) Вычитаемое – это число, которое вычитают из уменьшаемого.
3) Разность – это число, которое получается в результате вычитания, то есть ответ.
Рассуждаем.
Уменьшаемое – вычитаемое = разность
Уменьшаемое – разность = вычитаемое
Разность + вычитаемое = уменьшаемое
Делаем вывод.
Если к разности прибавить вычитаемое, получится уменьшаемое.
Номер 2.
Объясни решение уравнения и проверку.
Ответ:
x − 20 = 31
x = 31 + 20
x = 51
Проверка:
51 − 20 = 31
31 = 31
Чтобы решить уравнение, нужно найти неизвестное уменьшаемое. Для этого нужно к вычитаемому прибавить разность:
31 + 20 = 51
x = 51
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни названия компонентов при вычитании, и зависимость между компонентами и результатом действия вычитания.
Рассуждения.
x − 20 = 31
x − уменьшаемое, 20 − вычитаемое, 31 − разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
x = 31 + 20
x = 51
Делаем проверку.
Для проверки подставим полученный результат вместо х, то есть число 51.
Если правая и левая часть равны, то уравнение решено верно.
51 − 20 = 31
31 = 31 – верно
Оформляем задание в тетрадь
x − 20 = 31
x = 31 + 20
x = 51;
Проверка:
51 − 20 = 31
31 = 31
Ответ: 51.
Номер 3.
Реши уравнения с объяснением.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни названия компонентов при сложении и вычитании, и зависимость между ними.
Объяснения решения.
b − 8 = 54
b − уменьшаемое, 8 − вычитаемое, 54 − разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
b = 54 + 8
b = 62
x − 36 = 40
x − уменьшаемое, 36 − вычитаемое, 40 − разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
x = 40 + 36
x = 76
k + 14 = 20
k − первое слагаемое, 14 − второе слагаемое, 20 − сумма.
Чтобы найти первое слагаемое, нужно из 20 вычесть второе слагаемое.
k = 20 − 14
k = 6
Делаем проверку.
b − 8 = 54
62 – 8 = 54
54 = 54 – верно
x − 36 = 40
76 – 36 = 40
40 = 40 – верно
k + 14 = 20
6 + 14 = 20
20 = 20 – верно
Номер 4.
Запиши столбиком решение и проверку.
Ответ:
1) Помни, что складывать можно только единицы с единицами, а десятки с десятками. Вычитать тоже можно только единицы из единиц и десятки из десятков.
2) Помни, что 1 дес. = 10 ед.
Объяснение вычислений.
49 – 35
Вычитаем единицы. 9 – 5 = 4 – получилось единиц.
Записываем в разряде единиц число 4.
Вычитаем десятки. 4 – 3 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 14.
68 – 18
Вычитаем единицы. 8 – 8 = 0 – получилось единиц.
Записываем в разряде единиц число 0.
Вычитаем десятки. 6 – 1 = 5 – получилось десятков.
Записываем в разряде десятков число 5.
Читаем ответ: 50.
32 – 17
Вычитаем единицы. От числа 2 мы не можем отнять 7.
Занимаем 1 дес. = 10 ед., 10 + 2 = 12 ед., 12 – 7 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Вычитаем десятки. Было 3 дес., мы занимали 1 дес, осталось 3 – 1 = 2 дес.,
2 – 1 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 15.
80 – 65
Вычитаем единицы. От числа 0 мы не можем отнять 5.
Занимаем 1 дес. = 10 ед., 10 – 5 = 5 – получилось единиц.
Записываем в разряде единиц число 5.
Вычитаем десятки. Было 8 дес., мы занимали 1 дес, осталось 8 – 1 = 7 дес.,
7 – 6 = 1 – получилось десятков.
Записываем в разряде десятков число 1.
Читаем ответ: 15.
Оформляем задание в тетрадь
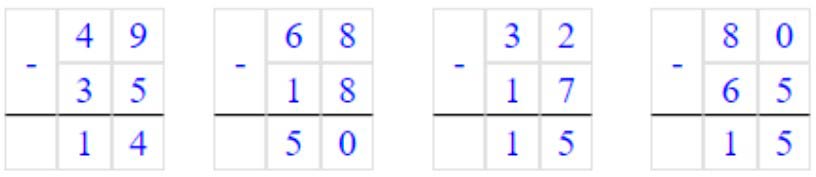
Делаем проверку.
Чтобы сделать проверку вычитания нужно к разности прибавить вычитаемое.
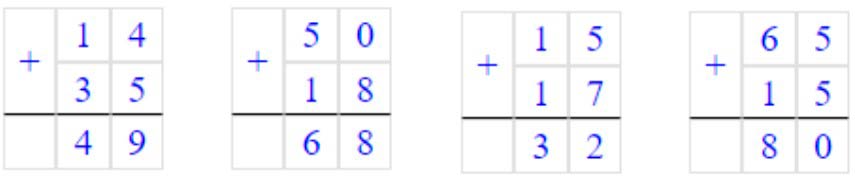
Номер 5.
Найди значения суммы и разности чисел b и 10 при b = 36, b = 57, b = 63, b = 10.
Ответ:
36 + 10 = 46 63 + 10 = 73
36 ‒ 10 = 26 63 ‒ 10 = 53
57 + 10 = 67 10 + 10 = 20
57 ‒ 10 = 47 10 ‒ 10 = 0
b – 10, значит, уменьшить число на 10 единиц.
b + 10, значит, увеличить число на 10 единиц.
Составляем выражения.
b – 10 - разность чисел b и 10
b + 10 – сумма чисел b и 10
Рассуждаем.
Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число.
Вычисляем значение выражения.
b – 10,
при b = 36, то 36 – 10 = (30 + 6) – 10 = (30 – 10) + 6 = 20 + 6 = 26
при b = 57, то 57 – 10 = (50 + 7) – 10 = (50 – 10) + 7 = 40 + 7 = 47
при b = 63, то 63 – 10 = (60 + 3) – 10 = (60 – 10) + 3 = 50 + 3 = 53
при b = 10, то 10 – 10 = 0
b + 10
при b = 36, то 36 + 10 = (30 + 6) + 10 = (30 + 10) + 6 = 40 + 6 = 46
при b = 57, то 57 + 10 = (50 + 7) + 10 = (50 + 10) + 7 = 60 + 7 = 67
при b = 63, то 63 + 10 = (60 + 3) + 10 = (60 + 10) + 3 = 70 + 3 = 73
при b = 10, то 10 + 10 = 1 дес. + 1 дес. = 2 дес. = 20
Номер 6.
Ответ:
1) Помни, сравнивать можно только числовые значения, выраженные в одних единицах измерения.
2) Помни, что 1 см = 10 мм
Рассуждаем.
7 + 7 < 7 + 7 + 7, так как 14 < 21
7 + 7 = 14
7 + 7 + 7 = 21
9 + 9 + 9 > 9 + 9, так как 27 > 18
9 + 9 + 9 = 27
9 + 9 = 18
2 см > 1 см 8 мм, так как 20 мм > 18 мм
2 см = 20 мм
3 см 6 мм < 4 см, так как 36 мм < 40 мм
4 см = 40 мм
Записываем сравнение в тетрадь.
7 + 7 < 7 + 7 + 7
9 + 9 + 9 > 9 + 9
2 см > 1 см 8 мм
3 см 6 мм < 4 см
Номер 7.
На клумбе расцвели 15 красных астр, розовых на 3 меньше, а белых астр столько, сколько красных и розовых вместе. Сколько белых астр?
Ответ:
1-й способ решения:

1) 15 − 3 = 12 (ас.) – розовых.
2) 15 + 12 = 27 (ас.) – белых.
Ответ: 27 белых астр расцвели на клумбе.
2-й способ решения: Решение с помощью выражения. 15 + (15 – 3) = 15 + 12 = 27 (а.) – белые. Ответ: 27 астр.
1) Первое действие вычисляется вычитанием
2) Второе действие вычисляется сложением.
Оформляем условие в виде краткой записи.
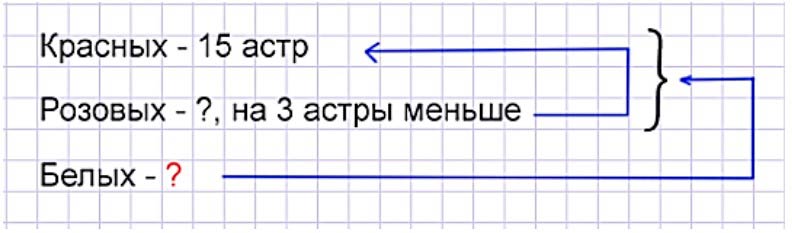
Рассуждаем.
Узнаем количество розовых астр.
Розовых астр расцвело на 3 меньше, чем красных. Значит, столько же, но без 3 астр. Поэтому, чтобы узнать, сколько розовых астр расцвело, нужно из количества красных вычесть 3 астры.
15 – 3 = 12 (астр) – розовых
Продолжим рассуждения.
Узнаем количество белых астр.
Белых астр расцвело столько, сколько красных и розовых вместе. Значит, нужно сложить количество красных и розовых астр.
15 + 12 = 27 (астр) – белых
Записываем ответ.
Ответ: 27 белых астр.
Решение с помощью выражения: 15 + (15 – 3) = 27 астр
где 15 – 3 – количество розовых астр.
Номер 8.
Ответ:
48 + 49 + 2 = 48 + 2 + 49 = 50 + 49 = 99
56 + 27 + 3 = 27 + 3 + 56 = 30 + 56 = 86
69 − (26 + 24) = 69 − 50 = 19
69 − 26 + 24 = 43 + 24 = 67
30 − 22 = 8
44 − 30 = 14
80 − 4 = 76
84 − 5 = 79
Вычисление значений выражения сводится к применению правил:
1) а + (в + с) = (а + в) + с – прибавления суммы к числу;
2) а – (в + с) = (а – в) – с – вычитания суммы из числа;
3) (а + в) – с = (а – с) + в – вычитания числа из суммы.
Устные рассуждения.
48 + 49 + 2 = (48 + 2) + 49 = 50 + 49 = (50 + 40) + 9 = 90 + 9 = 99
Применяем правило прибавления суммы к числу.
56 + 27 + 3 = (27 + 3) + 56 = 30 + 56 = (30 + 50) + 6 = 80 + 6 = 86
Применяем правило прибавления суммы к числу
69 − (26 + 24) = 69 − 50 = (60 + 9) – 50 = (60 – 50) + 9 = 10 + 9 = 19
Применяем правило вычитания числа из суммы
69 − 26 + 24 = 43 + 24 = 43 + (20 + 4) = (43 + 20) + 4 = 53 + 4 = 57
Применяем правило прибавления суммы к числу
30 − 22 = 30 – (20 + 2) = (30 – 20) – 2 = 10 – 2 = 8
Применяем правило вычитания суммы из числа
44 − 30 = (40 + 4) – 30 = (40 – 30) + 4 = 10 + 4 = 14
Применяем правило вычитания суммы из числа
80 − 4 = (70 + 10) – 4 = 70 + (10 – 4) = 70 + 6 = 76
Применяем правило вычитания суммы из числа
84 − 5 = 84 – (4 + 1) = (84 – 4) – 1 = 80 – 1 = 79
Применяем правило вычитания суммы из числа
Оформляем задание в тетрадь
48 + 49 + 2 = (48 + 2) + 49 = 50 + 49 = 99;
56 + 27 + 3 = 56 + (27 + 3) = 56 + 30 = 86;
69 − (26 + 24) = 69 − 50 = 19;
69 − 26 + 24 = 43 + 24 = 67;
30 − 22 = 8;
44 − 30 = 14;
80 − 4 = 76;
84 − 5 = 79.
Номер 9.
Какой из двух отрезков длиннее? Определи на глаз, а затем проверь измерением.

Ответ:
Синий отрезок – 4 см. Красный отрезок – 4 см. Отрезки равные друг другу.
1) Отрезок – геометрическая фигура, представляющая собой часть прямой, ограниченную с двух сторон точками. 2) Длина отрезка – расстояние между точками
Рассуждение.
Сравнить длины отрезков можно разными способами:
1) На глаз – способ, при котором сравнить длины отрезков можно только зрительно, примеркой.
2) Наложением – способ сравнения длин отрезков, при котором один отрезок накладывается на другой отрезок.
3) Измерением – способ, при котором используется линейка, и числовые значения длин фиксируются в определенных единицах измерения: миллиметрах, сантиметрах, и т.д.
Измерим длины отрезков с помощью линейки.
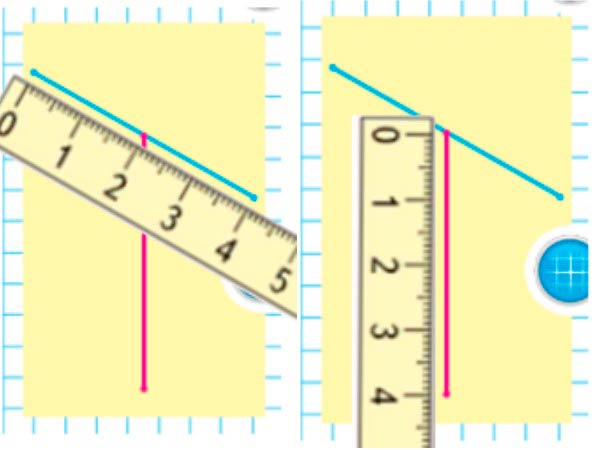
Делаем вывод.
Синий отрезок – 4 см
Красный отрезок – 4 см
4 см = 4 см - отрезки равны.
Ответ: отрезки раны.
Задание внизу страницы
Найди среди записей уравнение и реши его.
Ответ:
x − 6 = 54
x = 54 + 6
x = 60
Проверка
60 − 6 = 54
54 = 54
Ответ: х = 60
Уравнение: x − 6 = 54
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным или доказать, что такого неизвестного нет.
Рассуждения.
Признаками уравнения являются:
− наличие чисел
− наличие знаков арифметических действий
− наличие знака равно
− наличие неизвестной
Находим среди записей уравнение.
34 + х – выражение с неизвестной
16 + 13 = 29 – числовое равенство
78 – 25 = 53 – числовое равенство
х – 6 = 54 – уравнение
х + 3 > 2 – неравенство
х – 19 – выражение с неизвестной
Рассуждаем как решить уравнение.
x − 6 = 54
х – неизвестное уменьшаемое.
Чтобы найти уменьшаемое нужно к разности прибавить вычитаемое.
Решаем уравнение.
х – 6 = 54
x = 54 + 6
x = 60
Делаем проверку.
Для проверки подставим полученный результат вместо неизветного.
60 – 6 = 54
54 = 54 – верно.
Задание на полях страницы
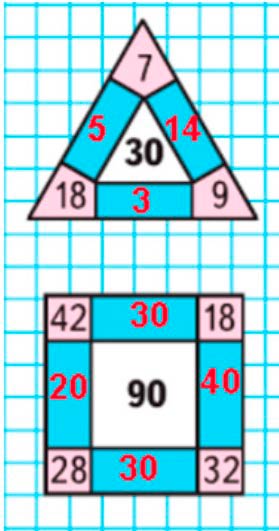
Занимательные рамки:

Ответ:

Занимательные рамки – это рамки, в которых сумма чисел, расположенных на одной прямой равна числу, записанному в центре.
Рассуждаем.
Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки.
Находим неизвестные числа.
Первая рамка:
18 + 15 + 7 = 30
18 + 13 + 9 = 30
7 + 14 + 9 = 30
Вторая рамка:
28 + 120 + 42 = 90
42 + 130 + 18 = 90
18 + 140 + 32 = 90
28 + 130 + 30 = 90
Заполняем рамку числами.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.