Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 70

Учебник 1 часть. Математика 3 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2023.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

Отличаются задания? Переключите год учебника.

2021 2023

математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 70

Номер 1.

Измерь длину и ширину класса. Узнай площадь класса в квадратных метрах.

Ответ:

Длина класса 8 м Ширина класса 4 м Вычисляю площадь класса: 8 ∙ 4 = 32 м² Ответ: площадь класса равна 32 м².

Подсказка:

1) 1 м² – это еще одна единица измерения площади.
2) Классная комната может иметь форму квадрата или прямоугольника.
3) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
4) Измерь длину и ширину класса с помощью рулетки.

Шаг 1.
Измерим ширину и длину класса.

Мы Вам представляем возможное решение данного задания.

Длина класса – 8 м
Ширина класса – 4 м
Значит класс имеет форму прямоугольника со сторонами 8 м и 4 м.

Шаг 2.
Вычислим площадь.

Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).

8 м · 4 м = (8 · 4) м² = 32 (м²) – площадь класса.

Номер 2.

1) Большие площади комнат, квартир, домов, земельных участков, городов и т. п. на бумаге изображают в уменьшенном виде. Например, на рисунке изображен план дачного участка, на котором за 1 м² условно принята одна клетка. Площадь дома на плане 42 клетки, значит, настоящая его площадь 42 м².
2) Найди по плану площадь сада.

Ответ:

9 ∙ 5 = 45 м². Ответ: площадь сада 45 м².

Подсказка:

1) 1 м² – это еще одна единица измерения площади.
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.

Шаг 1.
Рассмотрим рисунок.

На рисунке изображён план дачного участка. Нам нужно найти площадь сада.
Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Чтобы это сделать найдём длину и ширину сада на плане и на мместности.

Длина сада на плане равна 9 клеток, так как 1 клетка на плане равна 1 м на местности, значит:
9 · 1 м = 9 м – длина сада на местности.

Ширина сада на плане равна 5 клеток, так как 1 клетка на лпане равна 1 м на местности, значит:
5 · 1 м = 5 м – ширина сада на местности.

Шаг 2.
Найдём площадь сада.

Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).

9 ∙ 5 = 45 (м²) – площадь сада на местности.

Шаг 3.
Записываем ответ.

Ответ: площадь сада 45 м².

Номер 3.

Ответ:

Подсказка:

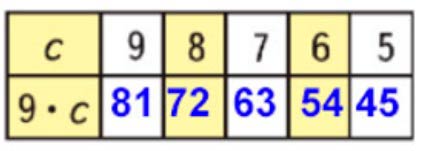
1) 9 · с, значит, число 9 умножить на с, т.е. увеличить в с раз.
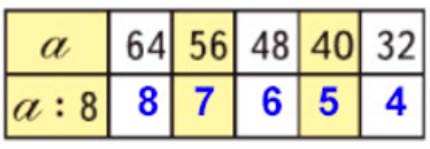
2) а : 8, значит, число а разделить на 8, т.е. уменьшить число в 8 раз.

Таблица 1.

Шаг 1.
Промежуточные вычисления.

Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.

9 · с, если:

с = 9, то 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.

с = 8, то 9 · 8 = 72,
где 9 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

с = 7, то 9 · 7 = 63,
где 9 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

с = 6, то 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

с = 5, то 9 · 5 = 45,
где 9 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

Шаг 2.
Заполним таблицу.

Таблица 2.

Шаг 3.
Промежуточные вычисления.

а : 8 , если:

а = 64, то 64 : 8 = 8, так как 8 · 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.

а = 56, то 56 : 8 = 7, так как 8 · 7 = 56,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.

а = 48, то 48 : 8 = 6, так как 8 · 6 = 48,
где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.

а = 40, то 40 : 8 = 5, так как 8 · 5 = 40,
где 8 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.

а = 32, то 32 : 8 = 4, так как 8 · 4 = 32,
где 8 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.

Шаг 4.
Заполним таблицу.

математика 3 класс Моро 1 часть страница 70. Год 2023

Страничка для любознательных

Номер 1.

Начерти такие фигуры в тетради. 1) Раздели фигуру 1 на три равные части так, чтобы линии деления шли по сторонам клеток. 2) Раздели фигуру 2 на четыре такие же части, как в предыдущем задании. Линии деления также должны идти по сторонам клеток.

Ответ:

Подсказка:

3 равные части, значит, имеющие равную площадь, т.е. состоящие из одинакового количества клеток и при наложении совпадающие.

Шаг 1.
Рассуждаем.

Фигура 1 состоит из 15 клеток. Эту фигуру нужно разделить на 3 одинаковые части. Значит, нам известно, сколько всего клеток в фигуре и на сколько частей нужно поделить фигуру, но не знаем сколько клеток будет в каждой части.
Что чтобы узнать сколько будет клеток в одной части нужно общее количество клеток разделить на количество частей.

15 : 3 = 5 (кл.) – будет в каждой части.

Значит фигуру 1 нужно разделить на 3 части, где в каждой части по 5 клеток.

Шаг 2.
Разделим фигуру 1 на 3 равные части.

Шаг 2.
Продолжим рассуждение.

Фигура 2 состоит из 20 клеток. Эту фигуру нужно разделить на 4 одинаковые части. Значит, нам известно, сколько всего клеток в фигуре и на сколько частей нужно поделить фигуру, но не знаем сколько клеток будет в каждой части.
Что чтобы узнать сколько будет клеток в одной части нужно общее количество клеток разделить на количество частей.

20 : 4 = 5 (кл.) – в каждой части.

Значит фигуру 2 нужно разделить на 4 части, где в каждой части по 5 клеток.

Шаг 3.
Разделим фигуру 2 на 4 равные части.

Номер 2.

Три друга: Кирилл, Алексей и Глеб – участвовали в теннисном турнире. Один из этих мальчиков стал победителем турнира. На вопрос: «Кто победил?» – Кирилл ответил: «Это не я». Алексей сказал: «Победителем стал Глеб». Позже выяснилось, что один из этих ответов верный, а другой нет. Кто победил в теннисном турнире?
Начни рассуждать так: «Предположим, что Алексей сказал правду, тогда и Кирилл...»

Ответ:

Предположим, что Алексей сказал правду, тогда и Кирилл сказал не правду, и победитель он, что невозможно.
Следовательно Кирилл сказал правду, а Алексей – не правду, а значит победитель Алексей.

Подсказка:

1) Перечислим еще раз все условия:
Кирилл ответил – «Победил не я»
Алексей сказал – «Победителем стал Глеб»
2) Рассуждай, и помни, что одно из вышеуказанных условий неверное, а другое – верное.

Шаг 1.
Оформляем условие в виде таблицы.

Всего было 3 мальчика, каждый из них может быть либо победителем, либо проигравшим.
Для решения задачи будем заполнять таблицу:

Шаг 2.
Рассуждаем.

Предположим, что Алексей был прав. Тогда, его утверждение «победителем стал Глеб» верно. Соответственно, в ячейку Глеб ставлю плюс, потому что он победил.

Шаг 3.
Продолжаем рассуждение.

По второму условию задачи одно из высказываний ложно, а второе – истинно. Значит, если высказывание Алексея истинно, то высказывание Кирилла ложно. И если «победил не я» - ложное высказывание, то Кирилл победил, но двух победителей быть не может. Значит, Алексей с самого начала был не прав.

Шаг 4.
Делаем вывод и записываем ответ.

Кирилл сказал правду, а Алексей – не правду, а значит победитель Алексей.
Ответ: победил Алексей.

Номер 3.

Мальчик купил несколько булочек по 17 р. Он подал в кассу 100 р. и получил сдачу в виде нескольких пятирублёвых монет. Сколько пятирублёвых монет он мог получить?

Ответ:

Если мальчик получил сдачу только пятирублёвыми монетами, то значит сумма покупки оканчивается на 5, следовательно мальчик мог купить только 5 булочек, и он потратил 17 ∙ 5 = 85 р., сдача составила 100 − 85 = 15 р., а количество пятирублёвых монет равно 15 : 5 = 3.

Подсказка:

Данная задача: вида «цена булочки, количество булочек, общая стоимость булочек» характеризуется зависимостями между компонентами:

Цена булочки · количество булочек = общая стоимость булочек.
Общая стоимость булочек : количество булочек = цена булочки.
Общая стоимость булочек : цена булочки = количество булочек.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Мальчик получил сдачу пятирублевыми монетами. Вспомним таблицу умножения 5:

5 · 1 = 5
5 · 2 = 10
5 · 3 = 15
5 · 4 = 20
5 · 5 = 25
5 · 6 = 30
5 · 7 = 35
5 · 8 = 40
5 · 9 = 45

Значит, сдачу он мог получить в виде числа, оканчивающегося на 0 или 5.

Шаг 3.
Продолжаем рассуждение.

Единственное, что нам осталось сделать – определить, при сложении 17 сколько раз, можно получить число, оканчивающееся на 0 или 5.
Найду это число, складывая это число разное количество раз:

17 + 17 = 34
34 + 17 = 51
51 + 17 = 68
68 + 17 = 85

Значит, было куплено 5 булочек.

Шаг 4.
Делаем проверку.

Проверяем, 17 · 5 = 85 рублей.
Сдача составит: 100 – 85 = 15 рублей.
А 15 рублей можно выдать пятирублевыми монетами.

Вычислим сколько будет пятирублёвых монет.
15 : 5 = 3 (мон.) – по 5 рублей.

Шаг 5.
Записываем ответ.

Ответ: 3 пятирублевые монеты.

Решение выражением: (100 – 17 ∙ 5) : 5 = 3 (монеты), где 100 – 17 · 5 – сдача.

Номер 4.

Используя в каждом случае 4 раза цифру 7, знаки арифметических действий и, если надо, скобки, составь 5 выражений со значениями: 5, 6, 7, 8, 9.

Например: 7 – (7 + 7) : 7 = 5.

Ответ:

7 – (7 + 7) : 7 = 5 (7 · 7 – 7) : 7 = 6 (7 – 7) · 7 + 7 = 7 (7 · 7 + 7) : 7 = 8 (7 + 7) : 7 + 7 = 9

Подсказка:

1) Перебирай все возможные арифметические действия, пока не найдешь верное решение.

2) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.

3) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.

4) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.

Шаг 1.
Составим выражения и расставим порядок действий.

3 2 1
7 − (7 + 7) : 7 = 5
В данном выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием выполняем вычитание.

1 2 3
(7 · 7 − 7) : 7 = 6
В данном выражении присутствуют действия вычитание, умножение и деление, а также скобки. Вначале выполняем действия в скобках – вначале умножение, а потом вычитание и последним действием выполняем деление.

1 2 3
(7 − 7) · 7 + 7 = 7
В данном выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, потом умножение и последним действием выполняем сложение.

2 1 3
(7 + 7 · 7) : 7 = 8
В данном выражении присутствуют действия сложение, умножение и деление, а также скобки. Вначале выполняем действия в скобках – вначале умножение, а потом сложение и последним действием выполняем деление.

1 2 3
(7 + 7) : 7 + 7 = 9
В данном выражении присутствуют действия сложения и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действие сложение вне скобок.

Шаг 2.
Вычислим по действиям.

3 2 1
7 − (7 + 7) : 7 = 5
1) 7 + 7 = 14
2) 14 : 7 = 2
3) 7 − 2 = 5

1 2 3
(7 · 7 − 7) : 7 = 6
1) 7 ∙ 7 = 49
2) 49 – 7 = 42
3) 42 : 7 = 6

1 2 3
(7 − 7) · 7 + 7 = 7
1) 7 – 7 = 0
2) 0 ∙ 7 = 0
3) 0 + 7 = 7

2 1 3
(7 + 7 · 7) : 7 = 8
1) 7 ∙ 7 = 49
2) 7 + 49 = 56
3) 56 : 7 = 8

1 2 3
(7 + 7) : 7 + 7 = 9
1) 7 + 7 = 15
2) 14 : 7 = 2
3) 2 + 7 = 9

Шаг 3.
Оформляем задание в тетрадь.

7 – (7 + 7) : 7 = 7 – 14 : 7 = 7 – 2 = 5

(7 · 7 – 7) : 7 = (49 – 7) : 7 = 42 : 7 = 6

(7 – 7) · 7 + 7 = 0 · 7 + 7 = 7

(7 · 7 + 7) : 7 = (49 + 7) : 7 = 56 : 7 = 8

(7 + 7) : 7 + 7 = 14 : 7 + 7 = 2 + 7 = 9

Конец страницы