Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 60

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Найди площадь каждого прямоугольника.

1-й способ решения:
В прямоугольнике AKMO в ряда по 6 квадратов площадью 1 см2. Площадь одного ряда 6 см2. В двух рядах уложится 6 ∙ 2 = 12 квадратов площадью 1 см2. Значит, площадь прямоугольника AKMO 12 см2.
В прямоугольнике LDCN по ширине умещается полоска из 2 клеток площадью 1 см2. По длине прямоугольника 3 см и такая полоска уложится 3 раза. Значит, во всем прямоугольнике уложится 2 ∙ 3 = 6 квадратов площадью 1 см2. Получается, площадь прямоугольника LDCN 6 см2.
2-й способ решения:
Прямоугольник АКМО:
Длина - 6 см
Ширина – 2 см
6 ∙ 2 = 12 (см2) – площадь АКМО.
Ответ: 12 см2
Прямоугольник LDCN:
Ширина – 2 см
Длина – 3 см
2 ∙ 3 = 6 (см2) – площадь LDCN
Ответ: 6 см2.
1) Площадь фигуры – часть плоскости, которую занимает фигура.
2) Чтобы вычислить площадь фигуры, нужно понять, сколько одинаковых квадратов помещается на плоскости.
3) Площадь фигуры измеряется в квадратных сантиметрах (см2).
Рассмотрим прямоугольник АКМО.
Прямоугольник АКМО состоит по длине из 6 квадратов площадью 1 см2.
Значит площадь такой полоски 6 см2:
1 · 6 = 6 см2.
По ширине такая полоска умещается 2 раза.
Значит площадь прямоугольника АКМО = 6 ∙ 2 = 12 см2
Рассмотрим прямоугольник LDCN.
В прямоугольнике LDCN по ширине умещается полоска из 2 квадратов площадью 1 см2:
1 · 2 = 2 см2.
По длине такая полоска умещается 3 раза.
Значит площадь LDCN = 2 ∙ 3 = 6 см2
Запишем ответ.
Ответ: площадь LDCN 6 см2, площадь LDCN – 6 см2.
Номер 2.
Пользуясь рисунком, узнай, площадь какого прямоугольника больше и на сколько квадратных сантиметров.

1-й способ решения: 1) 3 ∙ 2 = 6 (см2) – площадь первого прямоугольника. 2) 4 ∙ 3 = 12 (см2) – площадь второго прямоугольника. 3) 12 см2. − 6 см2. = 6 см2. – на сколько больше. Ответ: на 6 см2.
2-й способ решения:
4 ∙ 3 − 3 ∙ 2 = 6
Ответ: площадь второй фигуры больше площади первой на 6 см2.
Какова площадь первого прямоугольника?
3 ∙ 2 = 6 см2
Какова площадь второго прямоугольника?
4 ∙ 3 = 12 см2
На сколько см площадь первой фигуры меньше, чем площадь второй фигуры?
12 см2 − 6 см2 = 6 см2
1) Площадь фигуры измеряется в квадратных сантиметрах (см2).
2) Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
3) Чтобы узнать, на сколько площадь одной фигуры больше площади другой, нужно из площади большей фигуры вычесть площадь меньшей.
Рассмотрим первый прямоугольник.
Оформляем условие в виде краткой записи.
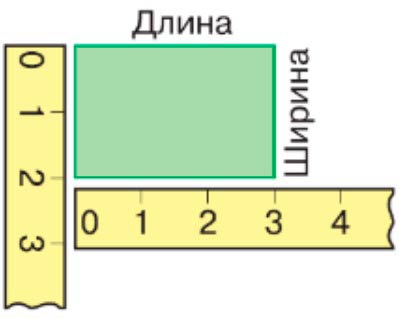
Длина – 3 см
Ширина – 2 см
Площадь – ?
Рассуждаем.
Надо найти площадь прямоугольника, длины сторон которого 3 см и 2 см. Разделим прямоугольник на квадраты площадью 1 см2 и узнаем,сколько всего таких квадратов в нём уложится.
По длине прямоугольника уложилось 3 квадрата площадью 1 см2. Площадь такой полоски 3 см2. При ширине прямоугольника 2 см такая полоска уложится в нём 2 раза.
Во всём прямоугольнике уложится 3 · 2 = 6 квадратов площадью 1 см2. 3 ∙ 2 = 6 (см2) – площадь первого прямоугольника.
Записываем ответ.
Ответ: площадь первого прямуогольника равна 6 см2.
Рассмотрим второй прямоугольник
Оформляем условие в виде краткой записи.
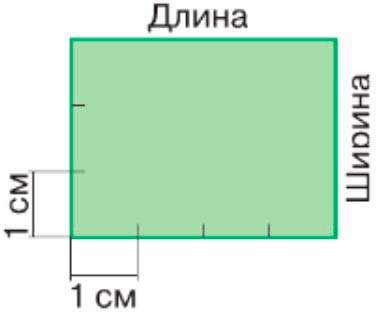
Длина – 4 см
Ширина – 3 см
Площадь – ?
Рассуждаем.
Надо найти площадь прямоугольника, длины сторон которого 4 см и 3 см. Разделим прямоугольник на квадраты площадью 1 см2 и узнаем,сколько всего таких квадратов в нём уложится.
По длине прямоугольника уложилось 4 квадрата площадью 1 см2. Площадь такой полоски 4 см2.
При ширине прямоугольника 3 см такая полоска уложится в нём 3 раза.
Во всём прямоугольнике уложится 4 · 3 = 12 квадратов площадью 1 см2.
4 ∙ 3 = 12 (см2) – площадь второго прямоугольника.
Запишем ответ.
Ответ: площадь второго прямуогольника равна 12 см2.
Узнаем площадь какого прямоугольника больше и на сколько.
Оформляем условие в виде краткой записи.
Рассуждаем.
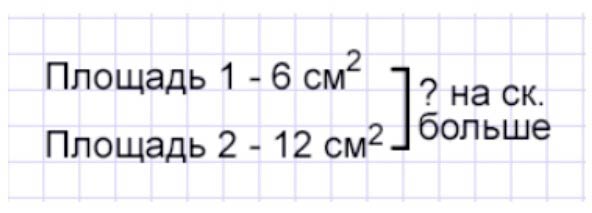
Сравниваем площади фигур. Чтобы узнать, на сколько площадь одной фигуры больше площади другой, нужно из большей площади вычесть площадь меньшей фигуры. Значит, из площади второй фигуры вычтем площадь первой фигуры.
2 – 6 = 6 (см2) – на сколько площадь второй фигуры больше площади первой фигуры.
Запишем ответ.
Ответ: площадь второй фигуры больше площади певрой фигуры на 6 см2.
Задание внизу страницы
Цепочка:

Ответ:
81 : 9 = 9 9 ∙ 6 = 54 54 + 18 = 72 72 : 8 = 9
1) Выполни действия по порядку.
2) Первая зеленая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполним устные рассуждения.
81 : 9 = 9,
так как 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 6 = 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
54 + 18 = 54 + (16 + 2) = (54 + 16) + 2 = 70 + 2 = 72
Представим число 18 в виде суммы чисел 16 и 2. Вначале к числу 54 прибавим число 16, а потом прибавим число 2.
72 : 8 = 9,
так как 8 · 9 = 72,
где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
81 : 9 = 9
9 ∙ 6 = 54
54 + 18 = 72
72 : 8 = 9
81 : 9 = 9 → 9 · 6 = 54 → 54 + 18 = 72 → 72 : 8 = 9
Номер 1.
72 : 9 7 · 9
54 : 6 2 · 8
79 - 16 + 40 : 8
70 - 49 : 7 - 30
56 : 8 8 · 8
63 : 9 7 · 7
72 : 9 = 8 7 ∙ 9 = 63
54 : 6 = 9 2 ∙ 8 = 16

56 : 8 = 7 8 ∙ 8 = 64
63 : 9 = 7 7 ∙ 7 = 49
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Выполним деление.
72 : 9 = 8, так как 8 · 9 = 72, где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
54 : 6 = 9, так как 6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Выполним умножение.
7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
2 · 8 = 16, где 2 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Выполним вычисления по действиям.
2 3 1
79 − 16 + 40 : 8 = 68
В данном выражении присутствуют действия сложение, вычитание и деление. Вначале выполняем деление, потом сложение и вычитание по порядку слева направо.
1) 40 : 8 = 5, так как 5 · 8 = 40
2) 79 – 16 = (70 – 10) + (9 – 6) = 60 + 3 = 63
Из десяток вычитаем десятки, а из единиц вычитаем единицы.
3) 63 + 5 = 68
2 1 3
70 – 49 : 7 – 30 = 33
В данном выражении присутствуют действия деления и вычитание. Вначале выполняем действие деление, а потом вычитание по порядку слева направо.
1) 49 : 7 = 7, так как 7 · 7 = 49
2) 70 − 7 = (60 + 10) – 7 = 60 + (10 – 7) = 60 + 3 = 63
Представим число 70 как сумму чисел 60 и 10. Из числа 10 вычтем число 7, а потом к полученной разности прибавим число 60.
3) 63 − 30 = 33
Вычислим деление.
56 : 8 = 7, так как 8 · 7 = 56, где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
63 : 9 = 7, так как 7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Вычислим умножение.
8 · 8 = 64, где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
7 · 7 = 49, где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
72 : 9 = 8
54 : 6 = 9
7 ∙ 9 = 63
2 ∙ 8 = 16
79 – 16 + 40 : 8 = 79 – 16 + 5 = 63 + 5 = 68
70 – 49 : 7 – 30 = 70 – 7 – 30 = 63 – 30 = 33
56 : 8 = 7
63 : 9 = 7
8 ∙ 8 = 64
7 ∙ 7 = 49
Номер 2.
Из 12 мотков шерсти получается 3 одинаковых детских свитера. 1) Сколько мотков шерсти потребуется на 5 таких свитеров? 2) Сколько таких свитеров можно связать из 16 таких мотков?
Ответ:
1) 12 : 3 = 4 (м.) – надо на один свитер.
2) 4 ∙ 5 = 20 (м.) – потребуется на 5 свитеров.
3) 16 : 4 = 4 (св.) – можно связать из 16 мотков.
Ответ: 20 мотков шерсти потребуется на 5 свитеров; 4 свитера можно связать из 16 мотков.
Данная задача: вида «расход шерсти на 1 свитер, количество свитеров, общее количество мотков» характеризуется зависимостями между компонентами:
Расход шерсти на 1 свитер · кол-во свитеров = общее кол-во шерсти.
Общее кол-во шерсти : расход шерсти на 1 свитер = кол-во свитеров.
Общее кол-во шерсти : кол-во свитеров = расход шерсти на 1 свитер.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
На 3 свитера израсходовали 12 мотков шерсти. Значит, известно количество связанных свитеров и общее количество шерсти, но неизвестен расход шерсти на 1 свитер. Из таблицы видно, что чтобы узнать, каков расход шерсти на 1 свитер, нужно общее количество шерсти разделить на количество свитеров.
12 : 3 = 4 (м.) – шерсти нужно на один свитер.
Продолжаем рассуждение.
Мы узнали, что на 1 свитер расходуется 4 мотка шерсти. Связали 5 свитеров, но общее количество шерсти неизвестно. При этом общее количество потраченной шерсти складывается из количества шерсти, расходуемой на каждый свитер. Поэтому, чтобы узнать, сколько мотков шерсти потратили, нужно сложить количество шерсти на каждый свитер. Но расход шерсти на свитер одинаковый. Поэтому, сложение одинаковых слагаемых можно заменить умножением.
4 ∙ 5 = 20 (м.) – потребуется на 5 свитеров.
Решение выражением.
12 : 3 ∙ 5 = 20 (м.), где 12 : 3 – шерсти нужно на один свитер.
Оформляем условие в виде таблицы.
-(2023).jpg)
Рассуждаем.
На 3 свитера израсходовали 12 мотков шерсти. Значит, известно количество связанных свитеров и общее количество шерсти, но неизвестен расход шерсти на 1 свитер. Из таблицы видно, что чтобы узнать, каков расход шерсти на 1 свитер, нужно общее количество шерсти разделить на количество свитеров.
12 : 3 = 4 (м.) – шерсти нужно на один свитер.
Продолжаем рассуждение.
Мы узнали, что на 1 свитер расходуется 4 мотка шерсти. Всего потратили 16 мотков шерсти, но сколько свитеров сшили – неизвестно. Значит, нам известен расход мотков шерсти, и общее количество шерсти, а неизвестно количество связанных свитеров. Соответственно, чтобы узнать, сколько свитеров связали, нужно общее количество шерсти разделить на расход шерсти.
16 : 4 = 4 (св.) – можно связать из 16 мотков шерсти.
Решение выражением.
16 : (12 : 3) = 4 (св.), где 12 : 3 - шерсти нужно на один свитер.
Номер 3.
Папа провёл 10 дней своего отпуска на даче, а остальные 2 недели в путешествиях с сыном по России. Сколько дней папа был в отпуске?
Ответ:Дача – 10 дн.
Путешествие – 2 нед. по 7 дн.
Всего – ? дн.
1) 7 ∙ 2 = 14 (дн.) – в путешествии по России
2) 10 + 14 = 24 (д.)
Ответ: 24 дня папа был в отпуске.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3, а – первый множитель, 3 – количество множителей.
Оформляем условие в виде краткой записи.
Дача – 10 дн.
Путешествие – 2 нед.
Всего – ? дн.
Рассуждаем.
Папа путешествовал по России 2 недели. В одной неделе 7 дней. Общее количество дней, проведенных в путешествии, складывается из количества дней в каждой из двух недель. Поэтому, чтобы узнать, сколько дней папа путешествовал с сыном по России, нужно сложить количество дней в двух неделях. Но количество дней в неделях одинаковое. Поэтому сложение одинаковых слагаемых можно заменить умножением.
7 ∙ 2 = 14 (дн.) – дом отдыха.
Продолжаем рассуждение.
Общее количество дней, проведенных папой в отпуске складывается из времени, проведенном на даче и в путешествии по России. Соответственно, чтобы узнать, сколько длился отдых, нужно сложить время, проведенное на даче и в путешествии.
10 + 14 = 24 (дн.) - папа был в отпуске.
Записываем ответ.
Ответ: 24 дня папа был в отпуске.
Решение выражением: 10 + 7 · 2 = 24 (дн.), где 7 · 2 – дни, проведенные в путешествии.
Номер 4.
Длина дорожки в саду 35 м. Миша расчистил от снега 7 м дорожки, Ира – 5 м, остальную часть дорожки расчистил папа. поставь вопрос и реши задачу, используя чертёж.

Сколько метров дорожки расчистил папа?
1) 7 + 5 = 12 (м) – расчистили дети.
2) 35 - 12 = 23 (м) – дорожки расчистил папа.
Ответ: 23 метра дорожки расчистил папа.
Вопрос: Сколько метров дорожки расчистил папа?
Оформляем условие в виде чертежа или краткой записи.
.jpg)
Рассуждаем.
Длина дорожки – 35 метров. Миша расчистил от снега 7 метров, а Ира – 5 метров. Общее количество расчищенной части складывается из части дороги, которую почистили Миша и Ира вместе. Поэтому, чтобы узнать, сколько метров дороги почистили Миша и Ира, нужно сложить части дорожки, которые почистили оба.
7 + 5 = 12 (м) – расчистили дети.
Продолжаем рассуждение.
Общая длина дорожки складывается из длины части дороги, которую уже расчистили и которую осталось расчистить папе. Поэтому, чтобы узнать, сколько метров дорожки осталось почистить папе, нужно из общей длины дороги вычесть почищенную часть.
35 − 12 = 23 (м) – дорожки расчистил папа.
Записываем ответ.
Ответ: 23 метра расчистил папа.
Решение выражением: 35 – (7 + 5) = 23 (м), где 7 + 5 – количество прочищенной дорожки детьми.
Номер 5.
Вырежи такие многоугольники и составь из них прямоугольник. Вычисли площадь и периметр этого прямоугольника.


Периметр: 4 + 4 + 2 + 2 = 12 (см)
Площадь: 4 ∙ 2 = 8 (см2)
1) Площадь фигуры измеряется в квадратных сантиметрах (см2).
2) Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (в одинаковых единицах), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади).
Составим из двух фигур прямоугольник.
.jpg)
Получится прямуогольник со сторонами 4 см и 2 см.
Найдём периметр.
Способ 1: сложить все стороны.
4 + 4 + 2 + 2 = (4 + 2) + (4 + 2) = 6 + 6 = 12 (см)
Споосб 2: по отдельности длину и ширину умножить на 2, а потом полученные произвдения сложить.
4 · 2 + 2 · 2 = 8 + 4 = 12 (см)
Споосб 3: сложить длину и ширину и полученную сумму умножить на 2.
(4 + 2) · 2 = 6 · 2 = 12 (см)
Найдём площадь.
У прямоугольника длина равна – 4 см, а ширина – 2 см. Значит для того чтобы вычислить площадь прямоугольника умножим длину на ширину.
4 · 2 = 8 см2 – площадь прямоугольника.
Запишем ответ.
Ответ: 12 см – периметр, 8 см2 площадь.
Задание внизу страницы.
30 : 5 9 ∙ 6
63 : 7 + 56 + 6
42 : 6 6 ∙ 6
30 : 5 = 6 9 ∙ 6 = 54

42 : 6 = 7 6 ∙ 6 = 36
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7, 8.
Вычислим деление.
30 : 5 = 6, так как 5 · 6 = 30, где 5 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Вычислим умножение.
9 · 6 = 6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых. Применяем переместительный закон умножения.
Расставим порядок действий и выполняем вычисления.
1 2 3
63 : 7 + 56 + 6 = 71
В данном выражении присутствуют действия сложения и деление. Вначале выполняем действие деление,
1) 63 : 7 = 9, так как 7 · 9 = 63
2) 9 + 56 = (5 + 4) + 56 = 5 + (4 + 56) = 5 + 60 = 65
Представим число 9 в виде суммы чисел 5 и 4. Вначале к числу 56 прибавим число 4, а потом прибавим число 5.
3) 65 + 6 = 65 + (5 + 1) = (65 + 5) + 1 = 70 + 1 = 71
Представим число 6 в виде суммы чисел 5 и 1. Вначале к числу 65 прибавим число 5, а потом прибавим число 1.
Вычислим деление.
42 : 6 = 7, так как 6 · 7 = 42, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполним умножение.
6 · 6 = 36, где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
30 : 5 = 6
9 ∙ 6 = 54
63 : 7 + 56 + 6 = 9 + 56 + 6 = 65 + 6 = 71
42 : 6 = 7
6 ∙ 6 = 36
Задание на полях страницы.
Цепочка:

63 : 7 = 9
9 ∙ 6 = 54
54 + 18 = 72
72 : 8 = 9
1) Выполни действия по порядку.
2) Первая зеленая шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
Выполняем вычисления с устными рассуждениями.
63 : 7 = 9, так как 7 · 9 = 63, где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
9 · 6 = 6 · 9 = 54, где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых. Применяем переместительный закон умножения.
54 + 18 = 54 + (16 + 2) = (54 + 16) + 2 = 70 + 2 = 72
Представим число 18 в виде суммы чисел 16 и 2. Вначале к числу 54 прибавим число 16, а потом прибавим число 2.
72 : 8 = 9, так как 8 · 9 = 72, где 8 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
63 : 7 = 9
9 ∙ 6 = 54
54 + 18 = 72
72 : 8 = 9
63 : 7 = 9 → 9 · 6 = 54 → 54 + 18 = 72 → 72 : 8 = 9
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.