Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 15

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 10.
В хозяйстве было 20 тракторов. На одно поле отправили 9 из них, на другое – столько же, а остальные были в ремонте. Сколько тракторов было в ремонте? Реши задачу разными способами.
Ответ:
Было – 20 тр.
Отправили – 9 тр. и 9 тр.
Осталось – ? тр.
1-й способ решения:
1) 9 + 9 = 18 (тр.) – отправили.
2) 20 − 18 = 2 (тр.)
2-й способ решения:
20 – 9 = 11 (тр.) – осталось после 1 раза.
11 – 9 = 2 (тр.)
Ответ: 2 трактора осталось в ремонте.
Решение задачи основывается на правиле:
а – (в + с) = (а – в) – с – вычитания суммы из числа.
Оформляем условие задачи.
Краткая запись:
Было – 20 тр.
Отправили на одно поле – 9 тр.
Отправили на другое поле – 9 тр.
Остались в ремонте – ? тр.
Рисунок.
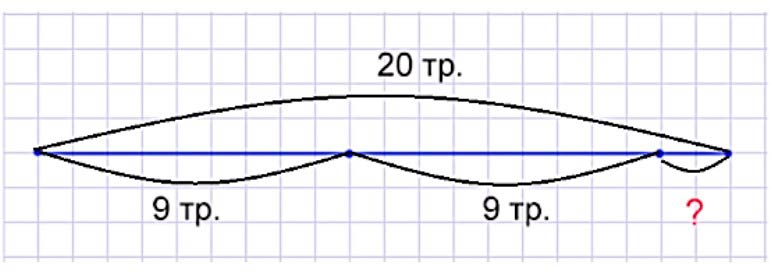
Рассуждаем.
В хозяйстве было 20 тракторов. На одно поле отправили 9 и на другое столько же. Столько же, значит, столько, сколько на первое, т.е. 9 тракторов.
Общее количество отправленных тракторов складывается из количества отправленных тракторов на первое и второе поле.
Для этого нужно сложить количества тракторов обоих полей.
9 + 9 = 18 (тр.) – отправили на два поля.
Продолжаем рассуждения.
Общее количество тракторов складывается из количества тракторов, которые отправили на поля и на ремонт. Поэтому, чтобы узнать, сколько тракторов отправили на ремонт нужно из общего количества тракторов отнять те, что отправили на поля.
20 - 18 = 2 (тр.) – отправили на ремонт
Записываем ответ.
Ответ: 2 трактора. Решение с помощью выражения: 20 – (9 + 9) = 2 (тр.)
Рассуждаем.
Узнаем сколько тракторов останется после отправки на первое поле. Чтобы это узнать нужно из общего количества тракторов отнять количество тракторов, отправленных на первое поле.
20 – 9 = 11 (тр.) – осталось.
Продолжаем рассуждения.
Теперь узнаем сколько останется тракторов после того как часть отправили на второе поле или сколько отправили на ремонт. На второе поле отправили столько же, сколько и на первое поле, это 9 тракторов. Чтобы это узнать нужно из оставшегося количества тракторов отнять количество тракторов, отправленных на второе поле.
11 – 9 = 2 (тр.) – отправили на ремонт.
Записываем ответ.
Ответ: 2 трактора.
Решение с помощью выражения:
20 – 9 – 9 = 2 (тр.)
Номер 11.
В одном бидоне было 48 л молока, в другом – столько же. Сколько литров молока осталось, когда продали 67 л?
Ответ:
Было – 48 л и 48 л
Продали – 67 л
Осталось – ? л
1-й способ решения:
1) 48 + 48 = 96 (л) – было в двух бидонах.
2) 96 − 67 = 29 (л)
Ответ: 29 литров молока осталось.
2-й способ решения: 1) 48 ∙ 2 = 96 (л) – было в двух бидонах. 2) 96 – 48 = 29 (л) – осталось молока. Ответ: 29 литров.
Решение задачи сводится к выражению:
(а + в) – с = (а – с) + в – правило вычитание числа из суммы.
Оформляем условие.
Краткая запись:
Было в одном бидоне – 48 л
Было в другом бидоне – 48 л
Продали – 67 л
Осталось – ? л
Рисунок:
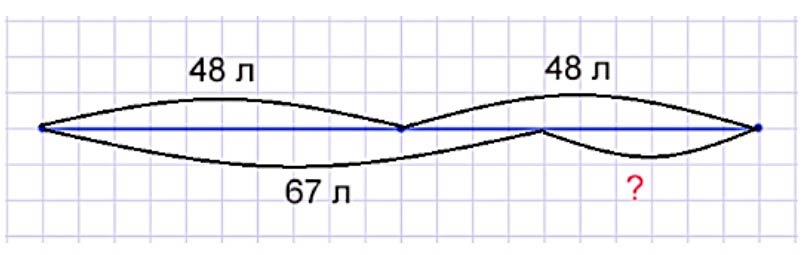
Рассуждаем.
Находим общее количество молока.
В первом бидоне было 48 литров молока, а во втором – столько же, значит тоже 48 литров.
Общее количество молока складывается из количества молока первого и второго бидона. Значит, нужно сложить количества молока обоих бидонов.
48 + 48 = 96 (л) – молока было в двух бидонах.
Продолжаем рассуждения.
Найдём сколько осталось молока.
Общее количество молока складывается из количества проданного молока и оставшегося. Поэтому, чтобы узнать, сколько молока осталось, нужно из общего количества молока вычесть количество проданного.
96 – 67 = 29 (л) – осталось молока.
Записываем ответ.
Ответ: 2 литров молока.
Решение с помощью выражения:
(48 + 48) – 67 = 29 (л.)
Вычислить значение данного выражения можно всего одним способом, поэтому и решение задачи существует только одно.
Номер 12.
Высота стола 7 дм, шкаф на 11 дм выше стола, а стул на 14 дм ниже шкафа. Узнай высоту стула.
Ответ:

1-й способ решения:
1) 7 + 11 = 18 (дм) – высота шкафа.
2) 18 − 14 = 4 (дм)
Ответ: 4 дм высота стула.
2-й способ решения: (7 + 11) – 14 = 18 – 14 = 4 (дм) – высота стула. Ответ: 4 дм.
1) Первое действие вычисляется сложением. 2) Второе действие вычисляется вычитанием.
Оформляем условие в виде краткой записи.
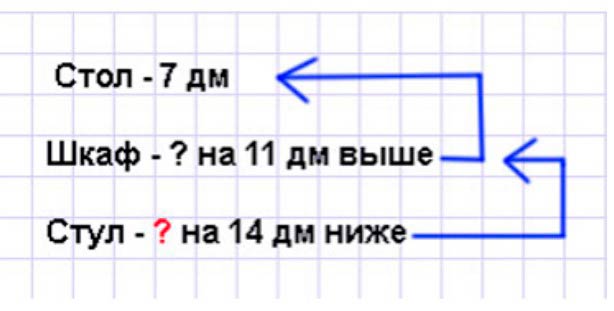
Рассуждаем.
Узнаем высоту шкафа.
Высота стола – 7 дм. Шкаф на 11 дм выше стола. Выше, значит, больше. Значит, что его высота такая же, как у стола и еще 11 дм. Поэтому, чтобы узнать, какова высота шкафа, нужно к высоте стола прибавить 11 дм.
7 + 11 = 18 (дм) – высота шкафа.
Продолжаем рассуждения.
Узнаем высоту стула.
Высота стула на 14 дм ниже, чем шкафа. Соответственно, высота стула такая же, как высота шкафа, но без 14 дм. Чтобы узнать, высоту стула нужно из высоты шкафа вычесть 14 дм.
18 − 14 = 4 (дм) – высота стула.
Записываем ответ.
Ответ: 4 дм.
Решение с помощью выражения:
(7 + 11) – 14 – 18 – 14 = 4 (дм), где 7 + 11 – высота шкафа.
Номер 13.
Масса поросенка 26 кг, гусь на 21 кг легче поросенка, а теленок на 47 кг тяжелее гуся. Найди массу теленка.
Ответ:

1-й способ решения:
1) 26 − 21 = 5 (кг) – масса гуся.
2) 5 + 47 = 52 (кг)
Ответ: 52 кг масса теленка.
2-й способ решения: 26 – 21 + 47 = 52 (кг) – масса теленка. Ответ: 52 кг.
1) Первое действие вычисляется вычитанием.
2) второе действие вычисляется сложением.
Оформляем условие в виде краткой записи.
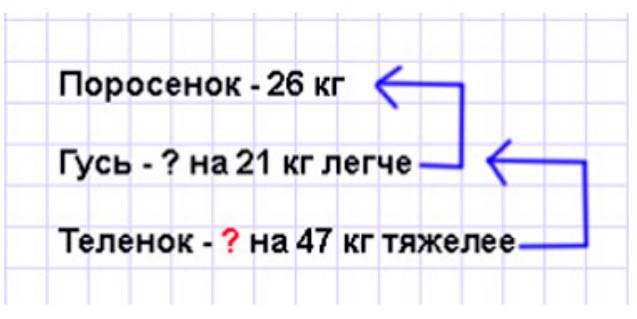
Рассуждаем.
Найдём массу гуся.
Масса поросенка – 26 кг, а гусь на 21 кг легче поросенка. Легче, значит, меньше. Масса гуся такая же, как поросенка, но без 21 кг.
Чтобы узнать, какова масса гуся, нужно из массы поросенка вычесть 21 кг.
26 − 21 = 5 (кг) – масса гуся.
Продолжаем рассуждения.
Найдём массу телёнка.
Теленок на 47 кг тяжелее гуся. Тяжелее, значит, больше. Поэтому масса теленка такая же, как масса гуся и еще 47 кг.
Чтобы узнать, какова масса теленка, нужно к массе гуся прибавить 47 кг.
5 + 47 = 52 (кг) – масса теленка.
Записываем ответ.
Ответ: 52 кг.
Решение с помощью выражения:
(26 – 21) + 47 = 52 (кг), где (26 – 21) – масса гуся.
Номер 14.
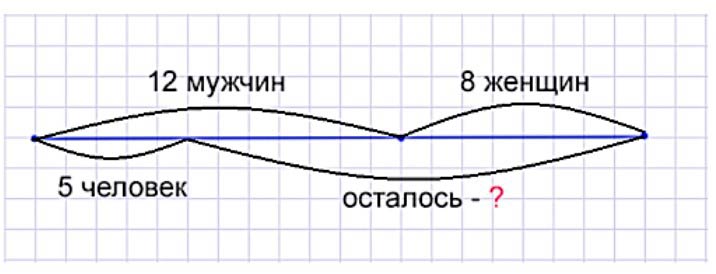
Дом ремонтировали 12 мужчин и 8 женщин. 5 человек из них перевели на другую работу. Сколько человек осталось ремонтировать дом?
Ответ:Было – 12 чел. и 8 чел. Перевели – 5 чел. Осталось – ? чел. 1) 12 + 8 = 20 (ч.) – всего ремонтировали дом. 2) 20 − 5 = 15 (ч.) Ответ: 15 человек осталось делать ремонт дома.
Решение задачи сводится к выражению, основанном на правиле.
(а + в) – с = (а – с) + в – вычитание числа из суммы.
Оформляем условие.
Краткая запись:
Было мужчин – 12 чел.
Было женщин – 8 чел.
Перевели – 5 чел.
Осталось – ?
Рисунок:
Рассуждаем.
Найдем общее количество человек.
Общее количество человек, которые ремонтировали дом, складывается из количества мужчин и женщин. Для этого нужно сложить количество мужчин и женщин.
12 + 8 = 20 (чел.) – всего ремонтировали дом.
Продолжаем рассуждения.
Узнаем сколько осталось.
5 человек перевели на другую работу. Перевели, значит, что их стало меньше.
Чтобы узнать, сколько людей осталось ремонтировать дом, нужно из общего количества людей вычесть количество переведенных.
20 − 5 = 15 (чел.) – осталось.
Записываем ответ.
Ответ: 15 человек.
Решение с помощью выражения:
(12 + 8) – 5 = 15 (чел.)
Рассмотрим все способы решения задачи.
Вычислить значение выражения можно тремя способами, поэтому и задачу можно решить тремя способами:
Решение 1:
(12 + 8) – 5 = 20 – 5 = 15
В первом действии вычисляем, сколько людей ремонтировали дом, а во втором – сколько людей осталось на стройке после перевода.
Решение 2:
(12 + 8) – 5 = (12 – 5) + 8 = 7 + 8 = 15
В первом действии вычисляем, сколько мужчин осталось на стройке после перевода, а во втором – сколько людей осталось всего вместе с женщинами.
Решение 3:
(12 + 8) – 5 = 12 + (8 – 5) = 12 + 3 = 15
В первом действии вычисляю, сколько женщин осталось на стройке после перевода, а во втором – сколько людей осталось всего вместе с мужчинами.
Номер 15.
Ответ:

Подробно:
27 + a
27 + 4 = 31
27 + 6 = 33
27 + 9 = 36
27 + 13 = 40
32 − c
32 − 4 = 28
32 − 6 = 26
32 − 9 = 23
32 − 13 = 19
1) 27 + а, значит, увеличить число на а единиц, т.е. прибавить а единиц.
2) 32 – с, значит, уменьшить число на с единиц, т.е. вычесть с единиц.
3) Вычисление значений выражения сводится к применению правил:
а + (в + с) = (а + в) + с – прибавления суммы к числу.
а – (в + с) = (а – в) – с – вычитания суммы из числа.
(а + в) – с = (а – с) + в – вычитания числа из суммы.
Рассуждаем.
Вместе неизвестного нужно подставить данное число и вычислить его значение.
27 + а
При а = 4, 27 + 4 = 27 + (3 + 1) = (27 + 3) + 1 = 30 + 1 = 31
Число 4 раскладываем на сумму чисел 1 и 3, после число 27 складываем с числом 3 и к полученной сумме прибавляем 1.
Применяем правило прибавление суммы к числу.
При а = 6, 27 + 6 = 27 + (3 + 3) = (27 + 3) + 3 = 30 + 3 = 33
Число 6 раскладываем на сумму чисел 3 и 3, после число 27 складываем с числом 3 и к полученной сумме прибавляем 3.
Применяем правило прибавление суммы к числу.
При а = 9, 27 + 9 = 27 + (3 + 6) = (27 + 3) + 6 = 30 + 6 = 36,
Число 9 раскладываем на сумму чисел 3 и 6, после число 27 складываем с числом 3 и к полученной сумме прибавляем 6.
Применяем правило прибавление суммы к числу.
При а = 13, 27 + 13 = 27 + (10 + 3) = (27 + 3) + 10 = 30 + 10 = 40
Число 13 раскладываем на сумму чисел 10 и 3, после число 27 складываем с числом 3 и к полученной сумме прибавляем 10.
Применяем правило прибавление суммы к числу.
32 – с
При с = 4, 32 – 4 = 32 – (2 + 2) = (32 – 2) – 2 = 30 – 2 = 28
Число 4 раскладываем на сумму чисел 2 и 2, после из числа 32 вычитаем число 2 и из полученной разности вычитаем 2.
Применяем правило вычитание суммы из числа.
При с = 6, 32 – 6 = 32 – (2 + 4) = (32 – 2) – 4 = 30 – 4 = 26
Число 6 раскладываем на сумму чисел 2 и 4, после из числа 32 вычитаем число 2 и из полученной разности вычитаем 42.
Применяем правило вычитание суммы из числа.
При с = 9, 32 – 9 = (22 + 10) – 9 = 22 + (10 – 9) = 22 + 1 = 23
Число 32 раскладываем на сумму чисел 22 и 10, после из числа 10 вычитаем число 9 и к полученной разности прибавляем число 22.<
Применяем правило вычитание числа из суммы.
При с = 13, 32 – 13 = 32 – (11 + 2) = (32 – 2) – 11 = 30 – 11 = 19
Число 13 раскладываем на сумму чисел 11 и 2, после из числа 32 вычитаем число 2 и из полученной разности вычитаем 11.
Применяем правило вычитания суммы из числа.
Заполним таблицу.

Номер 16.
В начале учебного года в классе было 20 учеников. В течение года 4 ученика перешли в другие школы. За это время в класс поступили 2 новых ученика. Поставь вопрос и реши задачу.
Ответ:
1-й способ решения:
Сколько учеников стало в классе к концу года?
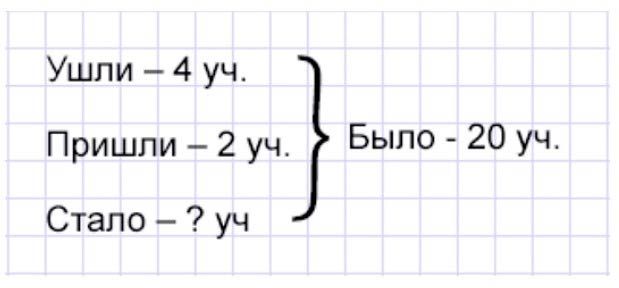
Было – 20 уч.
Ушли – 4 уч.
Пришли – 2 уч.
Стало – ? уч.
1) 20 − 4 = 16 (уч.) – стало учеников после ухода.
2) 16 + 2 = 18 (уч)
Ответ: 18 учеников стало в классе к концу года.
2-й способ решения:
Вопрос: К концу учебного года стало больше учеников или меньше? На сколько?
1) 20 – 4 + 2 = 18 (уч.) – осталось в конце учебного года.
2) 20 – 18 = 2 (уч.) – разница между началом года и концом года.
Ответ: к концу учебного года учеников стало меньше на 2 человека.
Вопрос к задаче: Сколько учеников стало в классе к концу учебного года?
Оформляем условие в виде краткой записи.
Рассуждаем.
Узнаем сколько стало учеников после ухода.
В классе было 20 учеников. В течение года 4 ученика перешли в другие школы, значит, учеников стало меньше.
Чтобы узнать, сколько учеников стало в классе, нужно из общего количества учеников вычесть те, что перешли.
20 − 4 = 16 (уч.) − стало после ухода.
Продолжаем рассуждения.
Узнаем сколько учеников стало в конце года.
Помимо этого, в класс поступили 2 новых ученика, значит их стало больше. Чтобы узнать, сколько учеников стало в классе, нужно к количеству учеников прибавить прибывших.
16 + 2 = 18 (уч.) − осталось в конце учебного года.
Запишем ответ.
Ответ: 18 учеников.
Решение с помощью выражения:
20 – 4 + 2 = 16 + 2 = 18 (уч.)
Номер 17.
1) Начерти отрезок МК длиной 4 см. Отметь его середину.
2) Начерти отрезок АВ длиной 60 мм. Отметь на нем точку С так, чтобы длина отрезка АС была равна 15 мм. Узнай длину отрезка СВ, не измеряя его.
1)

2)

60 − 15 = 45 (мм) – длина отрезка СВ. Ответ: 45 мм - длина отрезка СВ.
1) Отрезок – геометрическая фигура, представляющая собой часть прямой, ограниченную с двух сторон точками.
2) Длина отрезка – расстояние между точками.
3) Помни, что 1 см = 10 мм.
Рассуждаем.
Помни о соотношении сантиметров и клеток тетради. 1 сантиметр равен двум клеточкам тетрадного листа. Поэтому нужно начертить отрезок длиною 8 клеточкам тетради.
Чертим отрезок и отмечаем середину отрезка.
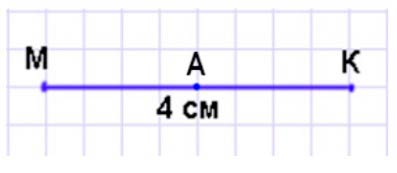
Середина отрезка – отметка, которая разбивает отрезок на две равные по длине части.
Значит делим отрезок 4 см пополам:
4 см : 2 = 2 см
От начала отрезка отмеряем 2 см или 4 клеточки, это и будет середина отрезка.
Рассуждаем.
Длина отрезка АВ складывается из длины отрезков АС и СВ. Значит, чтобы узнать, какова длина отрезка СВ, нужно из длины большего отрезка (АВ) вычесть известную длину отрезка (АС).
СВ = АВ – АС
Чертим и вычисляем.
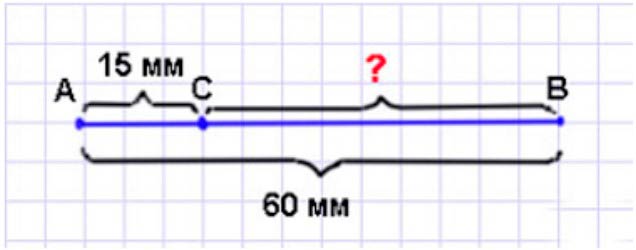
АВ = 60 мм = 6 см
АС = 15 мм = 1 см 5 мм
СВ = 60 мм – 15 мм = 45 мм = 4 см 5 мм
Задания на полях страницы
Набери 19:

Ответ:
8 + 7 + 4 = 19 8 + 8 + 3 = 19 7 + 7 + 5 = 19 10 + 9 = 19 10 + 7 + 2 = 19
Вспомни, что 1 дес. = 10 ед.
10 дес. = 1 сот.
Устные рассуждения.
Складывая данные числа нужно набрать число 19.
Оформляем задание в тетрадь.
8 + 7 + 4 = 19
8 + 8 + 3 = 19
7 + 7 + 5 = 19
10 + 9 = 19
10 + 7 + 2 = 19
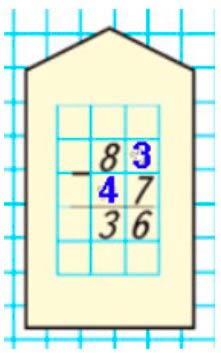
Ребус:

Ответ:

1) Помни, единицы можно складывать и вычитать только с единицами, десятки – с десятками.
2) 1 дес. = 10 ед.
3) Вспомни названия элементов при вычитании, и зависимость между ними:
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Рассуждаем.
1) Неизвестно количество единиц уменьшаемого.
Чтобы найти нужно количество единиц вычитаемого сложить со значением разности.
6 ед. + 7 ед. = 13 ед., т.е 1 дес. 3 ед.
Поэтому в уменьшаемом 3 единицы или вместит первой звездочки должна стоять цифра 3.
2) Неизвестно количество десятков уменьшаемого.
Чтобы найти нужно из количества десятков уменьшаемого вычесть количество десятков значения разности.
8 дес. – 3 дес. = 5 дес. да еще мы занимали 1 дес., то 5 дес. – 1 дес. = 4 дес.
Получаем равенство:
83 – 47 = 36.
Записываем решение в столбик.
Подставим вместо первой звёздочки цифру 3, а вместо второй – цифру 4.
Номер 5.
Рассмотри рисунок.
Выбери высказывания, верные для данного рисунка.
1) Каждая фигура красного цвета — шар.
2) Если фигура синего цвета, то это куб.
3) Кубов на рисунке столько же, сколько шаров.
Закончи высказывание, которое будет верным для этого рисунка:
Если фигура квадрат, то она ______________ .

1) Последняя фигура красного цвета не шар – неверное высказывание
2) На рисунке все кубы синего цвета – верное высказывание
3) На рисунке 2 куба, 1 шар – неверное высказывание
Ответ: верное высказывание 2
Если фигура квадрат, то она зеленого цвета
Вспомним, что мы знаем о кругах, шарах и многоугольниках.
Рассмотрим рисунок.
.jpg)
Выберем верные высказывания.
1) Последняя фигура красного цвета не шар – неверное высказывание.
2) На рисунке все кубы синего цвета – верное высказывание.
3) На рисунке 2 куба, 1 шар – неверное высказывание.
Запишем ответ.
Ответ: 2.
Если фигура квадрат, то она зеленого цвета.
Номер 6.
Старинная русская задача-загадка.
Прилетели галки, сели на палки. Если на каждой палке сядет по одной галке, то одна галка останется без палки. если на палке сядет по две галки, то одна палка останется без галки. Догадайся, сколько было галок и сколько было палок. Реши подбором.
Первое условие: на каждой палке сядет по одной галке, то одна галка останется без палки.
Если сядет: 2 галки и 1 палка
3 галки и 2 палки
4 галки и 3 палки
Второе условие: если на палке сядет по две галки, то одна палка останется без галки.
2 галки и 1 палка - не подходит, так как на палке сидит 2 галки
3 галки и 2 палки – не подходит, так как на одной палке будет 2 галки, а на одной палке еще одна галка останется.
4 галки и 3 палки – по 2 галки сядут на 2 палки и одна останется свободной.
Ответ: всего было 4 галки и 3 палки.
Метод подбора - это простой и эффективный способ разделения чисел. Суть его заключается в том, чтобы найти число, на которое нужно разделить заданное число, чтобы получить целое число без остатка. Для этого нужно последовательно пробовать делить заданное число на разные числа, начиная с наименьшего, и проверять, получается ли без остатка.
Разберем первое условие задания.
Первое условие: если на каждой палке сядет по одной галке, то одна галка останется без палки.
Если сядет:
2 галки и 1 палка.
3 галки и 2 палки.
4 галки и 3 палки.
Разберем второе условие задания.
Второе условие: если на палке сядет по две галки, то одна палка останется без галки.
2 галки и 1 палка – не подходит, так как на палке сидит 2 галки.
3 галки и 2 палки – не подходит, так как на одной палке будет 2 галки, а на одной палке еще одна галка останется.
4 галки и 3 палки – по 2 галки сядут на 2 палки и одна останется свободной.
Записываем ответ.
Ответ: 4 галки и 3 палки.
Номер 7.
Три одинаковых яблока и 1 груша весят столько же, сколько 19 слив. Три сливы и 1 яблоко весят столько же, сколько 1 груша. Сколько слив надо взять, чтобы уравновесить 1 грушу?

3 ябл. + 1 гр. = 19 сл.
1 гр. = 3 сл. + 1 ябл.
3 ябл. + 3 сл. + 1 ябл. = 19 сл.
4 ябл. = 19 сл. – 3 сл.
4 ябл. = 16 сл.
Ябл. = 16 сл. : 4
Ябл. = 4 сл.
1 гр. = 3 сл. + 4 сл. = 7сл.
Ответ: 7 слив нужно взять, чтобы уравновесить 1 грушу.
Равенство – запись, состоящая из математических выражений, между которыми ставится знак «=».
Рассуждаем.
3 ябл. + 1 гр. = 19 сл.
1 гр. = 3 сл. + 1 ябл.
3 ябл. + 3 сл. + 1 ябл. = 19 сл.
4 ябл. = 19 сл. – 3 сл.
4 ябл. = 16 сл.
Ябл. = 16 сл. : 4.
Ябл. = 4 сл.
1 гр. = 3 сл. + 4 сл. = 7сл.
Записываем ответ.
Ответ: 7 слив.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.