Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 104

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Что узнали. Чему научились
Номер 1.
С одной улицы вывезли 18 грузовых машин снега, а с другой – в 2 раза меньше. Сколько всего машин снега вывезли с двух улиц?
Ответ:
1-й способ решения:
1) 18 : 2 = 9 (м.) – снега вывезли со второй улицы.
2) 18 + 9 = 27 (шт.) – машин вывезли всего
Ответ: 27 машин снега вывезли с двух улиц.
2-й способ решения:
18 : 2 + 18 = 9 + 18 = 27 (м.) – вывезли с двух улиц.
Ответ: 27 машин снега.
1) «в 2 раза меньше», значит, вычисляется делением.
2) «всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.
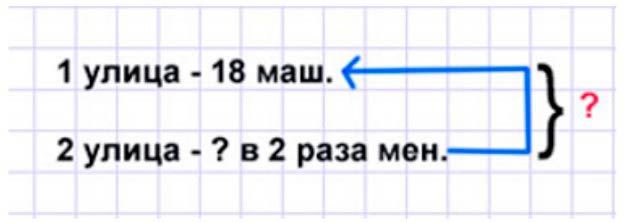
Рассуждаем.
С одной улицы вывезли 18 грузовых машин снега, а с другой – в 2 раза меньше. Значит, чтобы узнать, сколько грузовых машин вывезли с другой улицы, нужно количество вывезенного снега первой улицы разделить на 2.
18 : 2 = 9 (м.) – снега вывезли со второй улицы.
Продолжаем рассуждение.
Общее количество вывезенного снега складывается из количества вывезенного снега с первой улицы и второй. Значит, чтобы узнать, сколько снега вывезли всего, нужно сложить количества снега, которые вывезли с каждой улицы.
18 + 9 = 27 (м.) − вывезли с двух улиц.
Записываем ответ.
Ответ: 27 машин снега вывезли с двух улиц.
Решение выражением:
18 + 18 : 2 = 27 (м.), где 18 : 2 – количество вывезенного снега со второй улицы.
Номер 2.
Ребята расчищали от снега дорожки около школы. Мальчиков было 24, а девочек – в 3 раза меньше. Сколько всего ребят работало на расчистке дорожек от снега?
Ответ:
1-й способ решения:
1) 24 : 3 = 8 (чел.) – девочки.
2) 24 + 8 = 32 (чел.) – работали всего
Ответ: 32 человека работали на чистке дорожек от снега.
2-й способ решения:
24 : 3 + 24 = 8 + 24 = 32 (реб.) – всего детей.
Ответ: 32 ребят.
1) «в 3 раза меньше», значит, вычисляется делением.
2) «всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи.
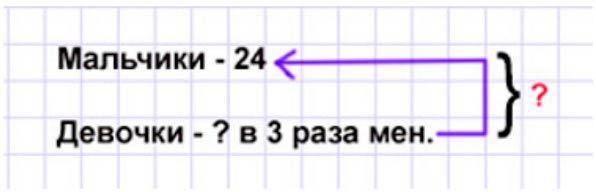
Рассуждаем.
Мальчиков на расчистке снега было 24, а девочек – в 3 раза меньше. Значит, чтобы узнать, сколько девочек было на уборке снега, нужно общее количество мальчиков разделить на 3.
24 : 3 = 8 (чел.) – было девочек.
Продолжаем рассуждение.
Мы узнали, что на расчистке было 24 мальчика и 8 девочек. Общее количество детей складывается из количества мальчиков и девочек. Значит, чтобы узнать, сколько детей было на расчистке снега, нужно сложить количество мальчиков и девочек.
24 + 8 = 32 (реб.) – всего детей.
Записываем ответ.
Ответ: 32 человека работали на чистке дорожек от снега.
Решение выражением:
24 + 24 : 3 = 32 (реб.), где 24 : 3 – количество девочек на расчистке снега.
Номер 3.
Длина класса ☐ м, а длина коридора в 5 раз больше длины класса. Дополни условие и узнай длину коридора.
Ответ:Длина класса 6 м. Какова длина коридора? 6 ∙ 5 = 30 (м) – длина коридора. Ответ: общая длина коридора составляет 30 метров.
1) «в 5 раз больше», значит, вычисляется умножением.
2) Задача: Длина класса 6 м, а длина коридора в 5 раз больше длины класса. Узнай длину коридора.
Оформляем условие в виде краткой записи.

Рассуждаем.
Длина класса – 6 метров, а коридора – в 5 раз больше.
«В 5 раз больше», значит, 5 раз по 6 метров. Значит, чтобы узнать, какова длина коридора, нужно длину класса умножить на 5.
6 ∙ 5 = 30 (м) – длина коридора.
Записываем ответ.
Ответ: 30 метров длина коридора.
Номер 4.
Ответ:2 см = 20 мм 3 м = 30 дм 8 дм = 80 см 6 см = 60 мм 5 м = 50 дм 1 дм = 100 мм
Помни о соотношении числовых значений единиц длины.
Устные рассуждения.
2 см = 2 · 10 мм = 20 мм, так как 1 см = 10 мм
6 см = 6 · 10 мм = 60 мм, так как 1 см = 10 мм
3 м = 3 · 10 дм = 30 дм, так как 1 м = 10 дм
5 м = 5 · 10 дм = 50 дм, так как 1 м = 10 дм
8 дм = 8 · 10 см = 80 см, так как 1 дм = 10 см
1 дм = 10 см = 100 мм, так как 1 дм = 10 см, а 10 см = 100 мм
Оформляем задание в тетрадь.
2 см = 2 ∙ 10 мм = 20 мм
6 см = 6 ∙ 10 мм = 60 мм
3 м = 3 ∙ 10 дм = 30 дм
5 м = 5 ∙ 10 дм = 50 дм
8 дм = 8 ∙ 10 см = 80 см
1 дм = 1 ∙ 100 мм = 100 мм
Номер 5.
Ответ:
1) 9 · а, значит, увеличить число 9 в а раз.
2) с : 7, значит, уменьшить число с в 7 раз.
Промежуточные вычисления.
Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.
9 · а, если:
а = 0, то 9 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
а = 1, то 9 · 1 = 9,
так как если любое число умножить на, то получится это же число.
а = 6, то 9 · 6 = 54,
где 9 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
а = 9, то 9 · 9 = 81,
где 9 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Заполним таблицу.
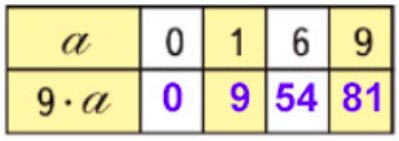
Промежуточные вычисления.
Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.
с : 7, если:
с = 0, то 0 : 7 = 0,
так как если 0 разделить на любое число, то получится 0.
с = 7, то 7 : 7 = 1,
так как если любое число разделить на само себя, то получится единица.
с = 28, то 28 : 7 = 4,
так как 7 · 4 = 28.
с = 63, то 63 : 7 = 9,
так как 7 · 9 = 63.
Заполним таблицу.
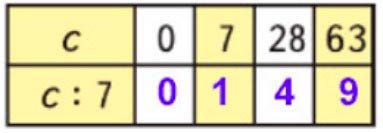
Номер 6.
Ответ:
1 ∙ 17 = 17 73 : 73 = 1 0 ∙ 92 = 0
98 ∙ 1 = 98 82 : 1 = 82 1 ∙ 65 = 65
1 ∙ 0 = 0 0 : 13 = 0
19 ∙ 0 = 0 0 : 1 = 0
1) Помни о том, что при умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Рассуждаем.
1 · 17 = 17,
так как если единицу умножить на любое число, то получится это же число.
98 · 1 = 98,
так как если любое число умножить на единицу, то получится это же число.
73 : 73 = 1,
так как если любое число разделить на само себя, то получится единица.
82 : 1 = 82,
так как если любое число разделить на единицу, то получится это же число.
0 · 92 = 0,
так как если 0 умножить на любое число, то получится 0.
1 · 65 = 65,
так как если единицу умножить на любое число, то получится это же число.
1 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
19 · 0 = 0,
так как если любое число умножить на 0, то получится 0.
0 : 13 = 0,
так как если 0 разделить на любое число, то получится 0.
0 : 1 = 0,
так как если 0 разделить на любое число, то получится 0.
Оформляем задание в тетрадь.
1 ∙ 17 = 17
98 ∙ 1 = 98
73 : 73 = 1
82 : 1 = 82
0 ∙ 92 = 0
1 ∙ 65 = 65
1 ∙ 0 = 0
19 ∙ 0 = 0
0 : 13 = 0
0 : 1 = 0
Номер 7.
При умножении каких двух однозначных чисел может получиться 12; 24; 27; 32; 49; 56; 63; 72?
Ответ:
12 = 2 ∙ 6
12 = 3 ∙ 4
24 = 6 ∙ 4
24 = 8 ∙ 3
27 = 9 ∙ 3
32 = 4 ∙ 8
49 = 7 ∙ 7
56 = 8 ∙ 7
63 = 7 ∙ 9
72 = 8 ∙ 9
Для выполнения задания обращайся к таблице умножения и деления на форзаце учебника.
Рассуждаем.
Число 12.
12 = 2 ∙ 6,
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
где 3 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
Число 24.
24 = 6 ∙ 4,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых. 27 = 9 ∙ 3,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
Число 32.
32 = 4 ∙ 8,
где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Число 49.
49 = 7 ∙ 7,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Число 56.
56 = 8 ∙ 7,
где 8 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Число 63.
63 = 7 ∙ 9,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Число 73.
73 = 8 ∙ 9,
где 68– одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Оформляем задание в тетрадь.
12 = 2 ∙ 6
12 = 3 ∙ 4
24 = 6 ∙ 4
24 = 8 ∙ 3
27 = 9 ∙ 3
32 = 4 ∙ 8
49 = 7 ∙ 7
56 = 8 ∙ 7
63 = 7 ∙ 9
73 = 8 ∙ 9
Номер 8.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий.
1 2
7 · 8 · 1 = 56
В данном выражении действия умножения. Выполняем действия по порядку слева направо.
1 2
5 · 9 · 0 = 0
В данном выражении действия умножения. Выполняем действия по порядку слева направо.
1 2
8 · 8 : 1 = 64
В данном выражении присутствуют действия умножение и деление – они равносильны. Выполняем действия по порядку слева направо.
1 2
49 : 7 · 9 = 63
В данном выражении действия умножения. Выполняем действия по порядку слева направо.
1 2
72 : 8 · 3 = 27
В данном выражении действия умножения. Выполняем действия по порядку слева направо.
1 2
56 : 7 · 2 = 16
В данном выражении действия умножения. Выполняем действия по порядку слева направо.
1 3 2
6 · 4 + 6 · 3 = 42
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а последним действием – сложение.
1 3 2
3 · 4 + 3 · 5 = 27
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а последним действием – сложение.
Складываем по разрядам: единицы складываем с единицами, а десятки – с десятками.
1 3 2
4 · 5 + 4 · 5 = 40
В данном выражении присутствуют действия сложение и умножения. Вначале выполняем действия умножения по порядку слева направо, а последним действием – сложение.
2 1
80 − 64 : 8 = 72
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
2 1
54 − 24 : 3 = 46
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
2 1
75 − 40 : 5 = 67
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
Выполняем вычисления по действиям.
1 2
7 · 8 · 1 = 56
1) 7 ∙ 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2) 56 ∙ 1 = 56,
так как если любое число умножить на единицу, то получится это же число
1 2
5 · 9 · 0 = 0
1) 5 ∙ 9 = 45,
где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
2) 45 ∙ 0 = 0,
так как если любое число умножить на 0, то получится 0
1 2
8 · 8 : 1 = 64
1) 8 ∙ 8 = 64,
где 8 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
2) 64 : 1 = 64,
так как если любое число разделить на единицу, то получится это же число.
1 2
49 : 7 · 9 = 63
1) 49 : 7 = 7, так как 7 · 7 = 49
2) 7 ∙ 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
1 2
72 : 8 · 3 = 27
1) 72 : 8 = 9, так как 8 · 9 = 72
2) 9 ∙ 3 = 27,
где 9 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
1 2
56 : 7 · 2 = 16
1) 56 : 7 = 8, так как 7 · 8 = 56
2) 8 ∙ 2 = 16,
где 8 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
1 3 2
6 · 4 + 6 · 3 = 42
1) 6 ∙ 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
2) 6 ∙ 3 = 18,
где 6 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
3) 24 + 18 = 42
1 3 2
3 · 4 + 3 · 5 = 27
1) 3 ∙ 4 = 12,
где 3 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
2) 3 ∙ 5 = 15,
где 3 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
3) 12 + 15 = (10 + 10) + (2 + 5) = 20 + 7 = 27 = 27
Складываем по разрядам: единицы складываем с единицами, а десятки - с десятками.
1 3 2
4 · 5 + 4 · 5 = 40
1) 4 ∙ 5 = 20,
где 4 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
2) 4 ∙ 5 = 20
3) 20 + 20 = 40
2 1
80 − 64 : 8 = 72
1) 64 : 8 = 8, так как 8 · 8 = 64
2) 80 − 8 = (70 + 10) – 8 = 70 + (10 – 8) = 70 + 2 = 72
2 1
54 − 24 : 3 = 46
1) 24 : 3 = 8, так как 3 · 8 = 24
2) 54 − 8 = 54 – (4 + 4) = (54 – 4) – 4 = (50 – 4) = 46
2 1
75 − 40 : 5 = 67
1) 40 : 5 = 8, так как 5 · 8 = 40
2) 75 − 8 = 75 – (5 + 3) = (75 – 5) – 3 = 70 – 3 = 67
Оформляем задание в тетрадь.
7 · 8 · 1 = 56 · 1 = 56
5 · 9 · 0 = 45 · 0 = 0
8 · 8 : 1 = 64 : 1 = 64
49 : 7 · 9 = 7 · 9 = 63
72 : 8 · 3 = 9 · 3 = 27
56 : 7 · 2 = 8 · 2 = 16
6 · 4 + 6 · 3 = 24 + 18 = 42
3 · 4 + 3 · 5 = 12 + 15 = 27
4 · 5 + 4 · 5 = 20 + 20 = 40
80 – 64 : 8 = 80 – 8 = = 72
54 – 24 : 3 = 54 – 8 = 46
75 – 40 : 5 = 75 – 8 = 70 – 3 = 67
Задания на полях страницы
Начерти.
Ответ:
Используй специальные приборы: циркуль и линейку.
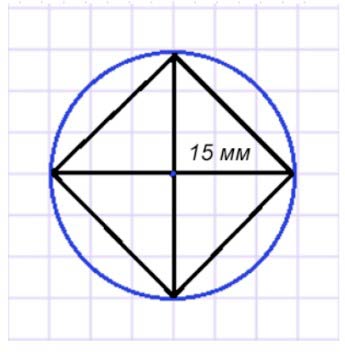
Рассмотрим фигуру.
Фигура состоит из окружности и внутри неё 4 треугольника, которые образуют квадрат.
Начертим окружность с радиусом 3 клетки = 15 мм = 1 см 5 мм.
Внутри начертим 4 треугольника с боковыми сторонами по 15 мм = 1 см 5 мм.
Сделаем построение.
Какое выражение лишнее?

48 : 6 – лишнее выражение, так его результат 8, а у других 9.
Чтобы понять, какое выражение лишнее, нужно проанализировать их все: на каком действии основаны, из каких компонентов состоят, каково их значение.
Рассуждаем.
Все выражения основаны на арифметическом действии – деление. Вычислим значения выражений:
54 : 6 = 9, так как 6 · 9 = 54
72 : 8 = 9, так как 8 · 9 = 72
48 : 6 = 8, так как 6 · 8 = 48
63 : 7 = 9, так как 7 · 9 = 63
45 : 5 = 9, так как 5 · 9 = 45
90 : 10 = 9, так как 10 · 9 = 90
81 : 9 = 9, так как 9 · 9 = 81
36 : 4 = 9, так как 4 · 9 = 36
Делаем вывод.
Лишнее выражение – 48 : 6, потому что его значение отличается от остальных, оно равно 8, а у остальных 9.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.