Математика 2 класс учебник Петерсон 2 часть ответы – страница 46

- Тип: ГДЗ, Решебник.
- Авторы: Петерсон Л. Г.
- Часть: 2.
- Год: 2021-2022.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 8.
Сравни:

Ответ:
Повторяются взаимосвязи между компонентами и результатами действий сложения и вычитания. Решение обосновывается с помощью логических рассуждений. При этом акцент делается не на формальное воспроизведение правил, а на смысл происходящих изменений. Например, постановку знака между выражениями 254 − a и 204 − a можно обосновать следующим образом: 254 − a > 204 − a, так как:
1) с увеличением уменьшаемого разность увеличивается;
2) чем больше было вначале, тем больше и останется;
3) в первом выражении уменьшаемое больше, чем во втором, а вычитаемое такое же, значит, и вся разность будет больше, и т.д.
В остальных примерах:
b − 287 < b − 56
c + d = d + c
m − 63 < m − 36
310 + n > 305 + n
440 − k < 540 − k
Номер 9.
Найди правило нахождения числа, помещённого в окошке чердака. Вставь число в свободное окошко.

Ответ:
Чтобы найти число, расположенное в окошке чердака, надо сложить числа, указанные на окнах дома, и из полученной суммы вычесть число, указанное на двери (72 + 27) − 43 = 56; (34 + 21) − 19 = 36. Следовательно, искомое число равно 287, так как (315 + 261) − 289 = 287.
Номер 10.
На рисунке изображена замкнутая ломаная линия, которая образовала лабиринт. Раскрась цветным карандашом область, границей которой является этот лабиринт.

Какие мыши находятся внутри области, а какие — снаружи? Покажи путь, по которому должна пройти мышь А, чтобы добраться до сыра. Какие ещё мыши могут добраться до сыра?
Ответ:
Внутри лабиринта находятся мыши B, C, D, E
Снаружи лабиринта находятся мыши А и М.
До сыра могут обежать мыши А и М.
Прямоугольный параллелепипед
Номер 1.
Найди на рисунке прямоугольные параллелепипеды. Является ли куб прямоугольным параллелепипедом?
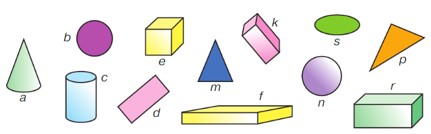
Прямоугольные параллелепипеды: e, k, f, r. Куб тоже является прямоугольным параллелепипедом.
Номер 2.
Рассмотри предмет формы прямоугольного параллелепипеда. Сколько у него граней, рёбер, вершин? Что ты замечаешь?
Ответ:Коробка имеет форму прямоугольного параллелепипеда. У него 6 граней, 8 вершин, 12 ребер.
Коробка, ящик, шкаф, кубики и многие другие предметы имеют форму прямоугольного параллелепипеда. У прямоугольного параллелепипеда 6 граней, 8 вершин и 12 рёбер.
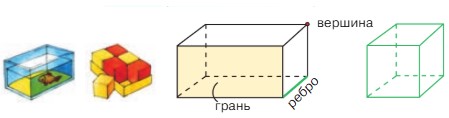
Куб тоже является прямоугольным параллелепипедом, но особым – у него все рёбра равны.
Номер 3.
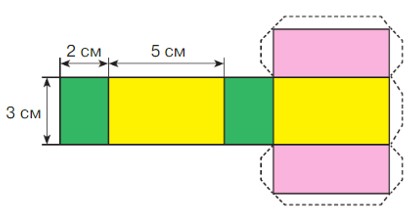
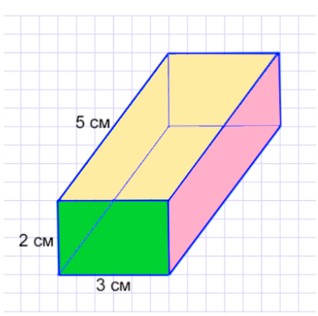
Практическая работа
Построй развертку прямоугольного параллелепипеда по данным размерам. Раскрась равные грани одним цветом.
Вырежи развертку из бумаги и склей.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.