Математика 2 класс учебник Моро, Волкова 2 часть ответы – страница 38

- Тип: ГДЗ, Решебник.
- Авторы: Моро М. И., Волкова С. И., Степанова С. В.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Номер 1.
Найди правила, по которым записаны числа:
1) в первой строке;
2) в каждом столбце.
Продолжи ряды чисел.
1) В первой строке числа записаны по правилу: + 10, + 1. 2) В каждом столбце числа записаны по правилу: − 10, − 1.

Рассмотри внимательно ряды чисел и установи закономерность.
Найдем правила по которым записаны числа
1) В первой строке числа записаны по правилу: + 10, + 1
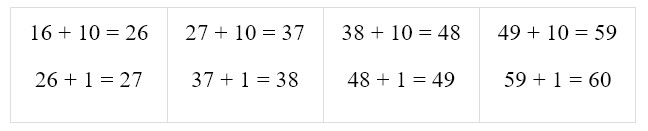
2) В каждом столбце числа записаны по правилу: - 10, - 1

Оформим задание в тетрадь
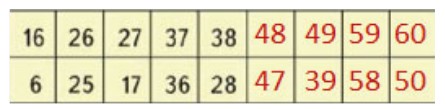
1) В первой строке числа записаны по правилу: + 10, + 1
2) В каждом столбце числа записаны по правилу: - 10, - 1
Номер 2.
Ученики лесной школы белка, еж, лиса и заяц начертили такие фигуры, по одной фигуре каждый.
Еж не стал чертить многоугольник, заяц не выбрал треугольник, а лиса начертила такой прямоугольник, у которого есть и свое название. Какую фигуру начертила белка?
Ёж не стал чертить многоугольник, значит он начертил круг. Лиса начертила прямоугольник у которого есть название, значит она начертила квадрат. Остались треугольник и прямоугольник. Заяц не выбрал треугольник, значит он начертил прямоугольник. Белка начертила треугольник.
Повтори материал о многоугольниках.
Рассуждаем

Ёж не стал чертить многоугольник, значит, он начертил КРУГ.
Лиса начертила такой прямоугольник, у которого есть и своё название. Это КВАДРАТ.
Остались треугольник и прямоугольник, но заяц не выбрал треугольник, значит, он начертил ПРЯМОУГОЛЬНИК.
Белка начертила ТРЕУГОЛЬНИК.
Оформим задание в тетрадь
Белка начертила треугольник.
Номер 1.
Выбери и расположи листочки, на которых записаны числовые выражения и буквы, так, чтобы значение каждого следующего выражения было на 7 меньше значения предыдущего.
Запиши в ряд значения выражений в нужном порядке, а под каждым из них - соответствующую букву. Из букв должно получиться название сказки.


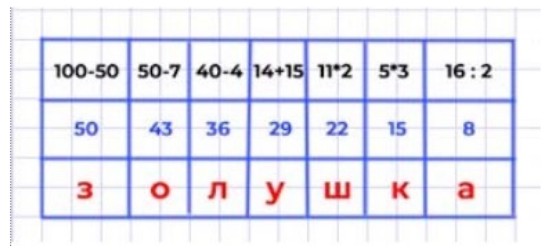
Выполним действия, чтобы прочитать название сказки.
Выполняем вычисления
100 – 50 = 50 (З)
50 – 7 = 43 (О)
40 – 4 = 36 (Л)
14 + 15 = 29 (У)
11 * 2 = 22 (Ш)
5 * 3 = 15 (К)
16 : 2 = 8 (А)
Оформляем задание в тетрадь
Номер 2.
Для украшения магазина купили 55 воздушных шаров красного и синего цвета. Синих шаров было меньше, чем красных, но их число записывалось теми же двумя цифрами, что и число красных шаров, но в обратном порядке. На сколько больше могло быть красных шаров, чем синих? Сколько ответов может быть в этой задаче?
Ответ:
Решаем задачу способом подбора.
Число шаров должно быть двузначным, ведь количество синих и красных шаров по условию записывалось двумя одинаковыми цифрами, но в обратном порядке, например, 17 – 71; 12 – 21 и т. д.
Работаем с первым десятком:
10, 11, 12, 13 – не подходят, ведь 10 – 01, 11 – 11 – не удовлетворяют условию задачи, а 12 – 21, 13 – 31 не дают в сумме 55.
15 – не подходит, ведь 15 – 51 больше, чем 55, значит 16, 17, 18 тоже не подходят.
А вот 14 и 41 подходят:
14 + 41 = 55 всего шаров.
41 − 14 = 27 – на столько красных шаров больше, чем синих.
Ответ: синих шаров 14, красных шаров 41.
Теперь работаем со вторым десятком: 20, 21, 22 – не подходят.
Подходит пара 23 и 32:
23 + 32 = 55 всего шаров.
32 − 23 = 9 – на столько шаров красных больше, чем синих.
Ответ: синих шаров 23, красных шаров 32.
2 ответа может быть в этой задаче.
Чтобы узнать, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
Решаем первым способом
Решаем задачу способом подбора.
Число шаров должно быть двузначным, ведь количество синих и красных шаров по условию записывалось двумя одинаковыми цифрами, но в обратном порядке, например, 17 – 71; 12 – 21 и т. д.
Работаем с первым десятком:
10, 11, 12, 13 – не подходят, ведь 10 – 01, 11 – 11 – не удовлетворяют условию задачи, а 12 – 21, 13 – 31 не дают в сумме 55.
15 – не подходит, ведь 15 – 51 больше, чем 55, значит 16, 17, 18 тоже не подходят.
А вот 14 и 41 подходят:
14 + 41 = 55 всего шаров.
41 − 14 = 27 – на столько красных шаров больше, чем синих.
Ответ: синих шаров 14, красных шаров 41.
Решаем вторым способом
Теперь работаем со вторым десятком: 20, 21, 22 – не подходят.
Подходит пара 23 и 32:
23 + 32 = 55 всего шаров.
32 − 23 = 9 – на столько шаров красных больше, чем синих.
Ответ: синих шаров 23, красных шаров 32.
Делаем вывод
В этой задаче может быть 2 ответа.
Оформляем задание в тетрадь
1 решение:
14 + 41 = 55 (ш)
14 < 41
14 синих шаров и 41 красный шар.
41 - 14 = 27 (ш)
Ответ: красных шаров на 27 больше, чем синих.
2 решение:
23 + 32 = 55 (ш)
23 < 32
23 синих шара и 32 красных шара.
32 - 23 = 9 (ш)
Ответ: красных шаров на 9 больше, чем синих.
Номер 3.
Запиши числа 4, 22, 0, 13, используя 4 раза цифру 1 и знаки действий.
Например: 11 - 11 = 0
1 + 1 + 1 + 1 = 4
11 + 11 = 22
1 − 1 = 0
11 + 1 + 1 = 13
Сложение – это арифметическое действие, с помощью которого из двух и более чисел получают новое, содержащее столько единиц, сколько было во всех данных числах вместе.
Выполняем вычисления
1 + 1 + 1 + 1 = 4
11 + 11 = 22
1 – 1 = 0
11 + 1 + 1 = 13
Оформляем задание в тетрадь
1 + 1 + 1 + 1 = 4
11 + 11 = 22
1 − 1 = 0
11 + 1 + 1 = 13
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.