Математика 2 класс учебник Моро, Волкова 1 часть ответы – страница 26

- Тип: ГДЗ, Решебник.
- Авторы: Моро М. И., Волкова С. И., Степанова С. В.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 1.
Прочитай задачи и реши их.
1) Вера купила блокнот за 6 р. и карандаш за 5 р. Сколько всего рублей стоили блокнот и карандаш вместе?
2) На 10 р. Вера купила блокнот и карандаш. Блокнот стоил 6 р. Сколько стоил карандаш?
3) На 10 р. Вера купила блокнот и карандаш. Карандаш стоил 4 р. Сколько стоил блокнот?
Рассмотри схемы к этим задачам и объясни, чем эти задачи похожи и чем различаются.
Задача 1:
6 + 4 = 10 (р.) – стоит блокнот и карандаш.
Ответ: 10 рублей стит блокнот и карандаш всего
Задача 2:
10 − 6 = 4 (р.) – стоит карандаш.
Ответ: 4 рубля стоит карандаш.
Задача 3:
10 − 4 = 6 (р.) – стоит блокнот.
Ответ: 6 рублей стоит блокнот.
Похожи эти схемы тем, что для них одни и те же значения слагаемых и суммы, но для первой задачи нужно найти сумму, а для второй и третьей разные неизвестные слагаемые.
Вид задачи: на нахождение целого по части
Условия задач оформляем в виде схематического рисунка.
Оформляем схематический рисунок
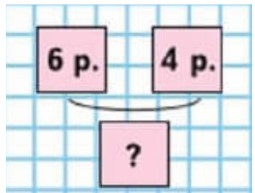
Рассуждаем
Чтобы узнать, сколько рублей стоили блокнот и карандаш вместе, нужно сложить их стоимости.
6 + 4 = 10 (р.) – стоят блокнот и карандаш вместе
Записываем ответ
Ответ: 10 рублей.
Оформляем схематический рисунок
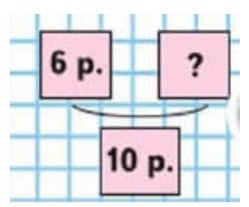
Рассуждаем
Чтобы узнать, сколько рублей стоил карандаш, нужно из общей стоимости блокнота и карандаша вычесть стоимость блокнота.
10 - 6 = 4 (р.) – стоит карандаш
Записываем ответ
Ответ: 4 рубля.
Оформляем схематический рисунок
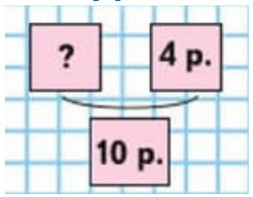
Рассуждаем
Чтобы узнать, сколько рублей стоил блокнот, нужно из общей стоимости блокнота и карандаша вычесть стоимость карандаша.
10 - 4 = 6 (р.) – стоит блокнот
Записываем ответ
Ответ: 6 рублей.
Номер 2.
Володя поймал 4 окуня и 3 леща. Сколько всего рыб он поймал? Реши задачу. Составь две задачи, обратные данной, и реши их.
Ответ:
4 + 3 = 7 (рыб) – всего поймал Володя.
Ответ: 7 рыб поймал Володя всего.
Обратная задача 1:
Володя поймал 7 рыб. Из них 4 окуня, а остальные – лещи. Сколько лещей поймал Володя?
7 − 4 = 3 (леща) – поймал Володя.
Ответ: 3 леща поймал Володя всего.
Обратная задача 2:
Володя поймал 7 рыб. Из них 3 леща, а остальные – окуни. Сколько окуней поймал Володя?
7 − 3 = 4 (окуня) – поймал Володя.
Ответ: 4 окуня поймал Володя всего.
Вид задачи: на нахождение целого по части
Условия задач оформляем в виде схематического рисунка.
Оформляем схематический рисунок и решаем 1-ю задачу
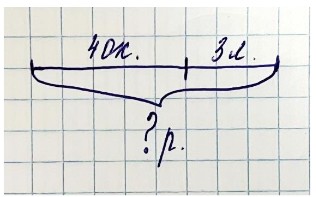
Рассуждаем
Чтобы узнать, сколько всего рыб поймал Володя, нужно сложить количество окуней и лещей.
4 + 3 = 7 (р.)- всего рыб поймал Володя
Записываем ответ
Ответ: 7 рыб.
Рассуждаем
Составим первую задачу, обратную данной.
Володя поймал 7 рыб. Из них 4 окуня, а остальные – лещи. Сколько лещей поймал Володя?
Оформляем схематический рисунок
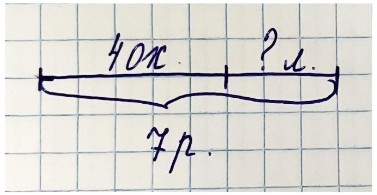
Рассуждаем
Чтобы узнать, сколько лещей поймал Володя, нужно из всего количества рыбы вычесть количество окуней.
7 - 4 = 3 (л.)- поймал Володя
Записываем ответ
Ответ: 3 леща.
Рассуждаем
Составим вторую задачу, обратную данной.
Володя поймал 7 рыб. Из них 3 леща, а остальные – окуни. Сколько окуней поймал Володя?
Оформляем схематический рисунок
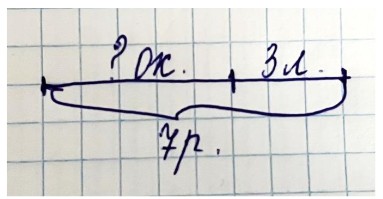
Рассуждаем
Чтобы узнать, сколько окуней поймал Володя, нужно из всего количества рыбы вычесть количество лещей.
7 - 3 = 4 (о.)- поймал Володя
Записываем ответ
Ответ: 4 окуня.
Номер 3.
Начерти два отрезка: один длиной 5 см, а другой на 10 мм короче. Запиши, чему равна длина второго отрезка в миллиметрах.
Ответ:5 см = 50 мм 50 мм − 10 мм = 40 мм 40 мм = 4 см

Оформляем условие задачи в виде краткой записи.
Оформим условие задачи в виде краткой записи
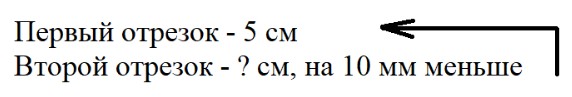
Рассуждаем
Для начала нам нужно перевести сантиметры в миллиметры.
5 см = 50 мм
Продолжаем рассуждение
Чтобы узнать, длину второго отрезка, из длины первого вычитаем 10 мм.
50 мм − 10 мм = 40 (мм)- длина второго отрезка
Начертим 2 отрезка
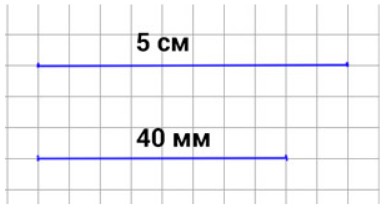
Записываем ответ
Ответ: 40 мм.
Номер 4.
Ответ:13 − 7 = 6 6 + 8 = 14 90 − 20 = 70 14 − 7 = 7 7 + 8 = 15 80 − 30 = 50 15 − 7 = 8 8 + 8 = 16 70 − 40 = 30 16 − 7 = 9 9 + 8 = 17 60 − 50 = 10
Рассмотри, как в каждом новом выражении изменяются компоненты, чтобы понять, как будет изменяться и значение и как проще вычислить их значения.
Выполним вычисления 1-го столбика
13 - 7 = 6
14 - 7 = 7
15 - 7 = 8
Исходя из решенных примеров, мы видим, что в каждом следующем примере меняется уменьшаемое, увеличиваясь на один, вычитаемое остается неизменным.
Значит, следующий пример будет:
16 - 7 = 9
Выполним вычисления 2-го столбика
6 + 8 = 14
7 + 8 = 15
8 + 8 = 16
Исходя из решенных примеров, мы видим, что в каждом следующем примере меняется первое слагаемое, увеличиваясь на один, второе слагаемое остается неизменным.
Значит, следующий пример будет:
9 + 8 = 17
Выполним вычисления 3-го столбика
90 - 20 = 70
80 - 30 = 50
70 - 40 = 30
Исходя из решенных примеров, мы видим, что в каждом следующем примере меняется уменьшаемое, оно уменьшается на 10, а вычитаемое увеличивается на 10.
Значит, следующий пример будет:
60 - 50 = 10
Номер 5.
У Юры, Димы и Алеши живут собаки: пудель, такса и овчарка, по одной у каждого мальчика. У Димы – не такса, у Юры – не овчарка и не такса. Какая собака у Алеши?
Ответ:
У Юры пудель (не овчарка и не такса).
У Димы овчарка (не такса).
Осталась такса, она у Алёши.
Подробное объяснение:
По условию, у Димы не такса. Значит, на пересечении имени Дима и таксы ставим крестик.
По условию, у Юры не овчарка и не такса. Значит ставим в колонке Юра крестик на овчарке и таксе.
А раз породы собак всего три, то у Юры пудель.
Раз у Юры пудель, то его не может быть у Димы и Алёши.
На пересечении Алёши, Димы и пуделя ставим крестик.
У Димы не пудель и не такса, значит, у него овчарка, а Алёше достаётся такса.

Составим таблицу по условию задачи
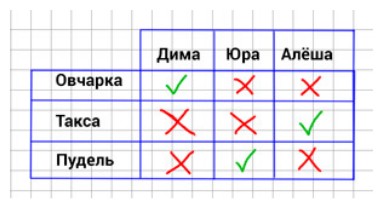
Рассуждаем
Исходя из таблицы, мы видим:
1) По условию, у Димы не такса. Значит, на пересечении имени Дима и таксы ставим крестик.
2) По условию, у Юры не овчарка и не такса. Значит, ставим в колонке Юра крестик на овчарке и таксе. А раз породы собак всего три, то у Юры пудель.
3) Раз у Юры пудель, то его не может быть у Димы и Алёши. На пересечении Алёши, Димы и пуделя ставим крестик. У Димы не пудель и не такса, значит, у него овчарка, а Алёше достаётся такса.
Задание внизу страницы
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.